해당 문제를 풀 수있는 방법은 다양하다고 생각했다. 내가 처음 선택한건무지성 백트래킹이었다.
질문게시판에 올라온 반례는 모두 통과 하였지만, 백준 체점에서는 번번히 메모리 초과가 발생하였다. 학교에서 보는 시험, 기관에서 보는 자격증 시험 등 모든 종류의 문제를 풀 때 가장 중요한 것은 출제자의 의도를 파악하는 것이다. 그래서 나는 출제자에게 굴복하고 다이나믹 프로그래밍을 활용해보기로 했다만... 정확히 할줄 모르는 나는 다른 풀이를 보고 내 나름대로 나의 것으로 만들었다. 계단오르기와 아주 유사한 문제인 포도주 시식도 함께 풀어 보겠다.
2579: 계단오르기
문제 분석
계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다.
도착점에 도달할때의 총 점수의 최대 값을 구해야 한다.
계단 오르는 데는 다음과 같은 규칙이 있다.
1. 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
2. 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
3. 마지막 도착 계단은 반드시 밟아야 한다.
1번째 조건을 보자면, 한 계단 or 두 계단 만 오를 수 있다고 했다. 간단한 조건이다.
2번째 조건은 조금 까다롭다. 연속된 세 개의 계단을 밟을 수 없다. 하지만 시작점은 포함되지 않는다. 그렇다면, 1번 계단과 2번 계단까지는 밟을 수 있다는 얘기이다.
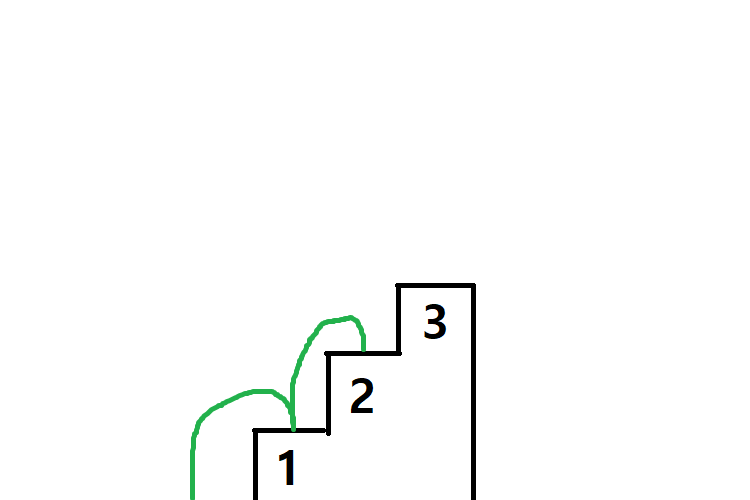
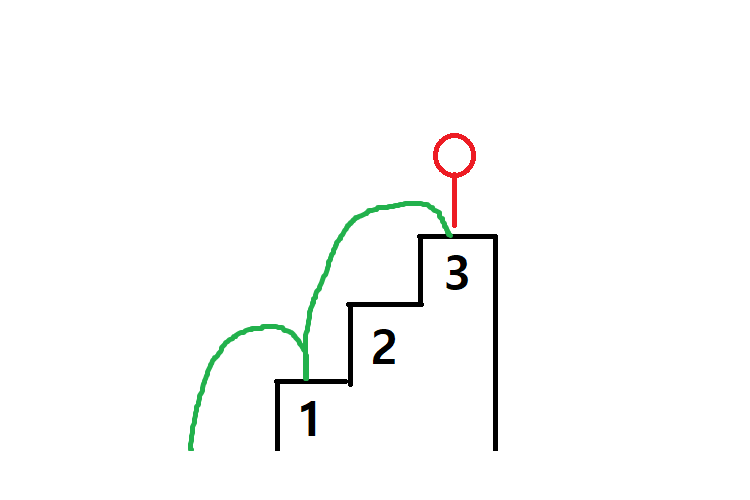
시작점을 포함한다면 3개의 스텝이 있었지만, 시작점을 포함하지 않으므로 해당 그림처럼 행동할 수 있다.
3번째 조건은 마지막 계단을 밟아야 한다고 한다. 위의 그림처럼 2연속으로 계단을 밟으면 마지막 계단을 밟을 수 없다. 3연속으로 계단을 밟아야 하기에, 2번째 조건 위반이다.
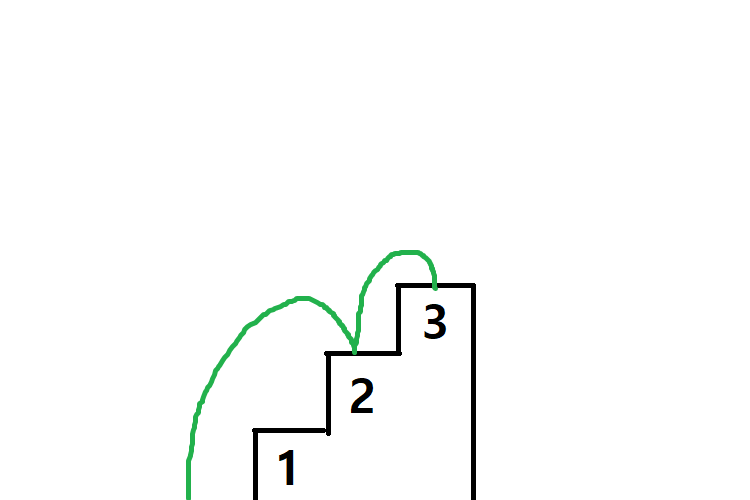
1. 시작점에서 두 계단을 오른 후 한 계단을 올라서 도착한다.
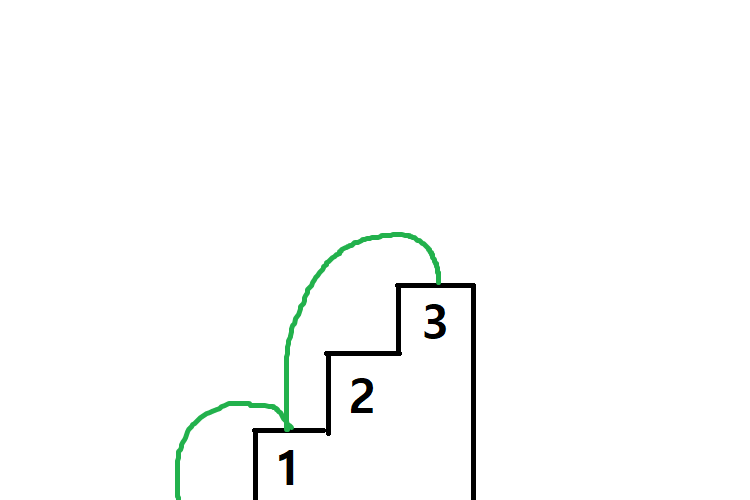
2. 시작점에서 한 계단을 오른 후 두 계단을 올라서 도착한다.
두가지의 경우가 존재한다.
이를 정리해보자면,
1번째 계단까지 오를 때의 최대 값은 첫번째 계단의 점수와 같다.
2번째 계단까지 오를 때의 최대 값은 첫번째, 두번째 계단의 점수의 합과 같다.
3번째 계단까지 오를 때의 최대 값은 위에서 설명했듯이2, 3번 계단의 합혹은1,3 계단의 합중 가장 큰 값과 같다.
자, 이제 1, 2, 3번째 계단까지의 최대 값을 구할 수 있게 되었다. 그렇다면 n번째 계단까지의 최대 값은 어떻게 구할까. n번째 계단에 올수있는 경우의 수는 두가지 밖에 없다.
- 두 계단을 오른 후 한 계단을 올라와 n번째 계단에 도착한다.
- 두 계단을 오른 후 한 계단을 오르니까, n-3번째 계단 부터 출발이다.
n-3번째 계단 까지의 최대 값 + n-1번째 계단의 점수 + n번째 계단의 점수가 최대값이 된다.
- 두 계단을 올라 n번째 계단에 도착한다.
- 첫번째 방법으로는,
두번째 방법으로는, 두 계단을 올라서 도착하니까, n-2번째 계단 부터 출발이다.
n-2번째 계단 까지의 최대 값 + n번째 계단의 점수가 최대값이 된다.
두가지 방법을 통해 구한 값중 큰 값이 n번째 계단 까지의 최대값이 된다.
이렇게 구상한 알고리즘을 코드로 작성해 보자.
DP[1] = arr[1]; //1번째 계단까지의 최대값
DP[2] = arr[1] + arr[2]; //2번째 계단까지의 최대값
DP[3] = max(arr[1], arr[2])+arr[3]; //3번째 계단까지의 최대값
.
.
.
DP[n] = max(DP[n-3] + arr[n-1], DP[n-2]) + arr[n];1, 2, 3번째 계단까지의 최대값을 알고 있으니, for문을 통해서 4번째, 5번째 ~ n번째 까지의 최대값을 구할 수 있다.
전체 코드
#include <iostream>
using namespace std;
int N;
int DP[301];
int arr[301] = {0, };
int main() {
cin >> N;
for(int i = 1; i <= N; i++)
cin >> arr[i];
DP[1] = arr[1];
DP[2] = arr[1] + arr[2];
DP[3] = max(arr[1], arr[2])+arr[3];
for(int i = 4; i <= N; i++)
DP[i] = max(DP[i-3] + arr[i-1], DP[i-2]) + arr[i];
cout << max(DP[N-1], DP[N]) << '\n';
}2156: 포도주 시식
문제 분석
포도주 잔을 선택하면 그 잔에 들어있는 포도주는 모두 마셔야 하고, 마신 후에는 원래 위치에 다시 놓아야 한다.
연속으로 놓여 있는 3잔을 모두 마실 수는 없다.
계단오르기 문제와 다른부분만 조건을 추가하면 끝이다.
- 시작하는 지점과 끝나는 지점이 정해져 있지않다.
- 엉뚱한 곳 부터 시작하면 최대 값이 될 수 없다. 1, 2, 3번째 까지는 동일하기에, 끝나는 부분만 고려해본다면 n개 까지의 최대값은 두가지 경우 밖에 없다.
max(DP[N-1], DP[N]);- 3연속만 안되는 제약만 있을 뿐, 두 칸, 세 칸, 네 칸 ~ 마구마구 건너띄어도 된다.
- 효율이 떨어지기 때문에 우리가 고려할 것은 세 칸 까지만이다. 즉, 한 칸 건너기, 두 칸 건너기, 두 칸 건너기 세가지 중 최대값을 저장하면 된다.
DP[n] = max(max(DP[n-4] + arr[n-1], DP[n-3] + arr[n-1]), DP[n-2]) + arr[n];전체 코드
#include <iostream>
using namespace std;
int N;
int DP[10001];
int arr[10001] = {0, };
int main() {
cin >> N;
for(int i = 1; i <= N; i++)
cin >> arr[i];
DP[1] = arr[1];
DP[2] = arr[1] + arr[2];
DP[3] = max(arr[1], arr[2])+arr[3];
for(int i = 4; i <= N; i++)
DP[i] = max(max(DP[i-4] + arr[i-1], DP[i-3] + arr[i-1]), DP[i-2]) + arr[i];
cout << max(DP[N-1], DP[N]) << '\n';
}