Learning rate Decay의 종류

이 글을 쓰게된 이유에는 Michigan 대학의 cs231n 강의에서 나오는 Learning rate Decay를 보고 해당 부분을 더 내것으로 만들고자 글을 작성합니다.

이 글에서 나오는 각 용어에 대해선 세부적인 설명보다는 어떠한 것이라는 부분에 대해서만 작성하고 용어에 대해선 깊이 들어가지 않습니다.

---

Learning Rate란?

Learning Rate란 딥 러닝 신경망이 확률적 경사 하강법(SGD : Stochastic Gradient Descent) 최적화 알고리즘을 사용하여 훈련하는데서 나온 파라미터이다.
좀 더 세부적으로 설명하면 다음과 같다.

• 모델의 weight이 업데이트 될 때마다 예상 오류에 대한 응답으로 모델을 조정하고 제어하면서 모델 학습에 영향을 주는 하이퍼 파라미터입니다.

여기서 하이퍼 파라미터(Hyper parameter)란

• 간단히 설명하자면 model에서 사용자가 직접 세팅해 주는 값이면 Hyper Parameter라고 생각하면 될 것 같습니다.

• 하이퍼 파라미터의 예시로는 Learning Rate, K-NN의 K의 값 등이 있습니다.

• Hyperparameter에 대한 추가적인 내용 : What is the Difference Between a Parameter and a Hyperparameter?

위의 내용을 참고하자면 Learning Rate란 모델을 다루는 사용자가 직접 세팅해 주는 값이면서 모델 학습에 영향을 주는 파라미터라고 이해하면 될 것 같습니다.

Learning Rate Decay

Learning Rate Decay는 기존의 Learning Rate가 높은 경우 loss 값을 빠르게 내릴 수는 있지만, 최적의 학습을 벗어나게 만들고 낮은 경우 최적의 학습을 할 수 잇지만 그 단계까지 너무 오랜 시간이 걸리게 됩니다.

따라서, 처음 시작시 Learning Rate 값을 크게 준 후 일정 epoch 마다 값을 감소시켜서 최적의 학습까지 더 빠르게 도달할 수 있게 하는 방법을 말합니다.

• 여기서는 5가지의 Learning rate Decay를 설명하겠습니다.

Learning Rate Decay - Step

---

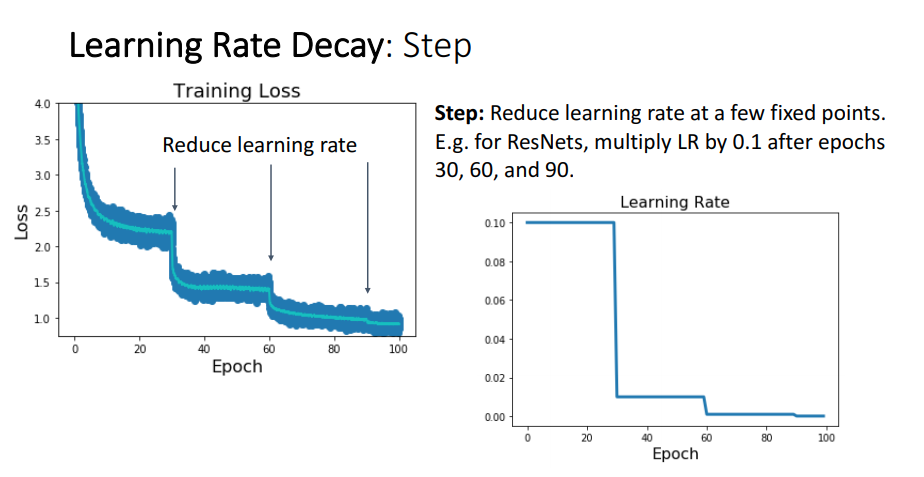
Step 방법으로 하는 Learning Rate Decay는 특정 epoch를 기준으로 learning rate을 감소시키는 것을 말합니다.

위의 예제 이미지에선 30 epoch 마다 Learning Rate를 감소 시켰고 그 비율은 0.1 * LR 입니다.
이렇게 특정 epoch 구간(step) 마다 일정한 비율로 감소 시켜주는 방법을 Step Decay라고 부릅니다.

위의 방법에 대한 결과를 loss 그래프로 볼때 learning rate가 감소함에 따라 큰 폭으로 0으로 향하는것을 볼 수 있죠.

Step Decay는 위의 결과를 보면 loss가 좋은 방향으로 향하는것은 맞지만, loss가 연속적이지 않은 부분이 있습니다.

그리고 stpe decay를 하려면 사용자들이 세팅해줘야하는 Hyper parameter가 기존의 Learning Rate에 추가로 감소 비율(예제에선 0.1), 몇 epoch 구간(stpe)마다 감소를 시킬 것인지를 정해주어야 했습니다.

Step Decay를 사용하면 기존보다 생각해야하는 Hyper Parameter가 늘어나니 세팅해야하는 값들이 증가하고 세팅 값의 경우의 수가 더 많이 생기게 되었습니다.

따라서 당시 사람들은 Hyper Parameter를 조금 덜 사용할 수 있는 다른 방법을 찾게 되었습니다.

그렇게해서 나온 연속적인 방법이 바로 Cosine Decay 입니다.

Learning Rate Decay - Cosine

---

수식에서 나오는 각 변수들 :

• ${a_0}$ = learning_rate에 초기 값

• T : 전체 Train epoch의 수

• t : 현재 epoch

위의 총 3가지의 parameter에서 t는 epoch가 반복함에 따라 값이 자동으로 증가되니 사용자는 ${a_0}$와 T 이 2가지 요소에 대해서만 learning rate를 생각하면 됩니다.

위의 Cosine Decay의 loss 그래프를 보면 위의 Step Decay와는 달리 안정적으로 끊김없이 loss가 감소하는 것을 볼 수 있습니다.

그리고 cosine decay 수식 ${a_t = {{1 \over 2} a_0} (1 \ + cos(t \pi \ / \ T)) }$에서 $a_0$, $T$ 이 2개의 요소만 사용자가 세팅을 하면 되어서 Step Decay 보다 Hyper Parameter에 대해 덜 생각할 수 있게 되었습니다.

Hyper Paremeters를 좀 덜 사용하고 learning rate도 연속적으로 사용하니 Cosine Decay를 Learning Rate Decay로 좀 더 고려를 많이 한다고 합니다.

Learning Rate Decay - Linear

---

위의 Cosine decay와 더불어 다른 연속적인 Learning Rate Decay를 생각했는데 그 중 하나가 Linear Decay 입니다.

Linear Decay의 parameter은 위와 동일하고 수식은 보다 간단히 ${a_0{(1-t/T)} }$로 되어 있습니다.

Learning Rate Decay - Inverse Sqrt

---

그리고 다른 연속적인 Learning Rate Decay로 Inverse Sqrt(Inverse Square Root) Decay가 있습니다.

Inverse Sqrt Decay는 수식을 보면 $t$ 역 제곱근의 ${a_0}$로 나타내어 집니다.

그리고 Cosine decay와 비슷한 Learning rate 그래프를 나타내지만, Cosine decay보다 Inverse Sqrt Decay가 더 빠르게 감소 되는것을 알 수 있습니다.

위의 이유로 Learning Rate Decay를 고려할 때 Inverse Sqrt보다 Cosine decay가 parameter space를 더 넓게 탐색한다고 생각을하고 Cosine decay를 더 많이 사용한다고 합니다.

Learning Rate Decay - Constant

---

마지막으로 흔히 사용되는 Learning Rate 방식으로 Learning Rate로 지정한 상수값을 계속 사용하는 것을 나타냅니다.

위의 Learning Rate 그래프를 보면 Rate가 일정함에도 Learning Rate Decay라고 굳이 CS231n에서 표현한 이유가 있습니다.

강의를 진행하신 강의자 분인 Justin Johnson께서 앞서 나온 Learning Rate Decay와 같은 "복잡한 learning rate를 사용할 경우 결과가 더 나아질 수는 있지만, 가능한한 빨리 무언가를 작동하고자할 때는 LR를 일반적인 상수로 두고 하는것도 좋은 선택이다."라고 말씀을 하셨습니다.

그리고 Adam 같은 경우 일반적인 상수를 하는것이 더 나은 결과가 나올 수 있다고도 얘기를 하셨습니다.

• 이 얘기를 듣고 지금까지 모델 학습을 했던것을 생각해보면 Learning rate가 Accuracy에 영향을 미치긴 해도 절대적인 요소는 아니긴 했습니다.
  
  모델링을 할 때 Learning Rate를 어떻게 해야할지 신경쓰는것 보다 '모델의 구조를 어떻게 만들지', '데이터는 어떤 데이터를 사용하고 전처리는 어떻게 할지' 등이 Accuracy에 영향을 주었던 것 같습니다.

제 생각이지만, Constant가 나온 이유는 모델의 Learning rate를 어떻게 하지 고민하기 전에 우선 모델이 제대로 만들어 졌는지, 데이터는 안전한지 등을 확실하게 하고 그 후에 Hyper Parameter 들을 조정해서 더 좋은 결과를 만들고 모델을 학습시킬 때의 시간 소요를 줄이는 것이 중요하다고 생각되어서 Constant를 얘기한것 같습니다.

---

Reference

CS231n 강의를 보고 제가 이해한 내용으로 글을 작성했습니다.

참조 : (CSs231n) Lecture 11: Training Neural Networks II