안정 정렬
- 안정 정렬(Stable Sort)란 중복된 값을 입력 순서와 동일하게 정렬합니다.
중복된 값을 입력 순서와 동일하게 정렬이라는 말은 기존의 다른 요소로 정렬이 된 입력값을 정렬을 할 때 기존의 정렬 형태를 유지한 상태에서 정렬을 한다는 의미와 같습니다.
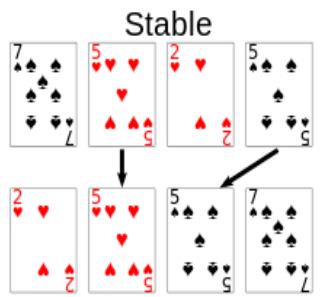
안정 정렬은 위와 같이 spades(♠), hearts(♥)의 문양을 가진 카드들이 있습니다.
여기서 문양이 다르지만 중복된 숫자인 경우 5 hearts(♥)가 5 spades(♠)보다 앞에 위치해 있습니다.
안정 정렬이 되려면, 입력 값에서 중복된 숫자인 5의 경우 정렬을 하고난 후에도 5 hearts(♥) -> 5 spades(♠) 순으로 정렬이 되어 있어야 합니다.
그럼 이제 아래의 오름차순 정렬을 하고 난 후의 결과를 보면 2 -> 5 -> 5 -> 7로 숫자가 오름차순에 형태를 가지면서, 기존의 입력 순서인 5 hearts(♥) -> 5 spades(♠) 순으로 정렬이 되어 있는것을 확인할 수 있습니다.
- 안정정렬(Stable sort)
중복된 값의 경우 입력 순서와 동일하게 유지해서 정렬 하는 것을 말합니다.
불안정 정렬
- 불안정 정렬(unStable Sort)란 중복된 값을 입력 순서와 상관없이 무작위로 뒤섞인 상태에서 정렬이 이루어 집니다.

위에 안정 정렬에선 중복된 값인 5가 5 hearts(♥) -> 5 spades(♠) 순으로 입력이 이루어 졌으니 정렬을 하고난 후에도 5 hearts(♥) -> 5 spades(♠)로 이루어 졌습니다.
그렇지만, 불안정 정렬의 경우 중복된 값을 입력 순서와 상관없이 무작위로 뒤섞인 상태에서 정렬을 합니다.
입력 값에 오름차순 정렬을 해서 2 -> 5 -> 5 -> 7의 결과에서 입력 순서가 영향을 끼치지 않으니 5 spades(♠) -> 5 hearts(♥)의 순서로 정렬이 되어 있는것을 알 수 있습니다.
- 불안정 정렬(unStable Sort)
중복된 값의 경우 입력 순서를 무작위로 뒤섞은 상태에서 정렬 하는 것을 말합니다.
위에 카드에 대한 비유를 지역별 택배 발송 시간의 표로 나타내면 다음과 같습니다.
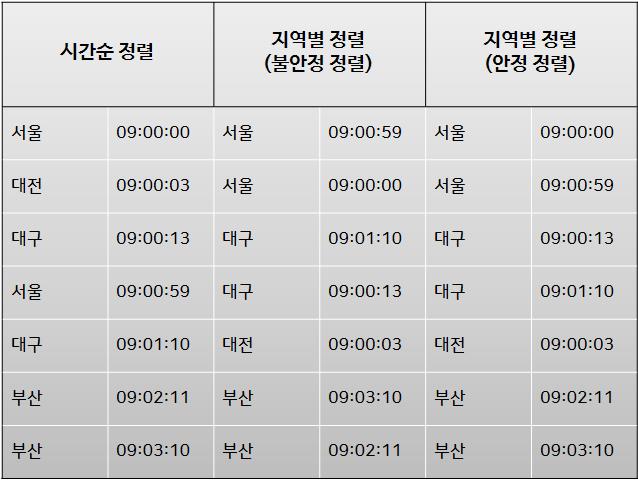
초기에 입력값은 시간순으로 정렬이 되어 있는 형태입니다.
이 입력 값을 서울 -> 대구 -> 대전 -> 부산 순서로 정렬 한다고 할 때
안정 정렬의 경우 중복된 값 즉 같은 지역에 경우 더 빠른 시간 순서로 정렬이 됩니다.
불안정 정렬의 경우 같은 지역에서 더 빠른 시간 순서로 정렬되는 것이 아닌 무작위로 섞여서 정렬을 하기에 시간 순서로 정렬이된 입력 값의 형태가 지역별 정렬을 거치면서 유지되지 않게 됩니다.
-
안정 정렬의 경우
시간 순서로 정렬을 해서 입력을 하는 경우 시간 순으로 입력이 이루어 지기에 중복 값의 경우에서도 시간 순으로 정렬을 한다. -
불안정 정렬의 경우
시간 순서로 정렬을 해서 입력을 하는 경우 시간 순으로 입력이 이루어 지지만 무작위로 뒤섞여서 정렬을 진행하기에 중복 값의 경우에선 시간 순의 정렬을 유지하기가 힘들다.
다양한 정렬 알고리즘
안정 정렬 알고리즘
-
삽입(Insertion) 정렬
- 최선 시간복잡도 :
- 평균 시간복잡도 :
- 최악 시간복잡도 :
-
버블(Bubble) 정렬
- 최선 시간복잡도 :
- 평균 시간복잡도 :
- 최악 시간복잡도 :
-
병합(Merge) 정렬
- 최선 시간복잡도 :
- 평균 시간복잡도 :
- 최악 시간복잡도 :
- 메모리 :
불안정 정렬 알고리즘
-
선택(Selection) 정렬
- 최선 시간복잡도 :
- 평균 시간복잡도 :
- 최악 시간복잡도 :
-
퀵(Quick) 정렬
- 최선 시간복잡도 :
- 평균 시간복잡도 :
- 최악 시간복잡도 :
- 메모리 : ~
-
힙(Heap) 정렬
- 최선 시간복잡도 :
- 평균 시간복잡도 :
- 최악 시간복잡도 :
-
인트로(Intro) 정렬
퀵 정렬에 힙 정렬을 더한 형태
기본적으로 퀵정렬을 하지만 재귀가 깊어지는 경우 힙 정렬을 사용한다.- 최선 시간복잡도 :
- 평균 시간복잡도 :
- 최악 시간복잡도 :
- 메모리 :
