[알고리즘과 자료구조] 이진 탐색 트리 알아보기

📖 '누구나 자료구조와 알고리즘'책을 공부한 내용을 담고 있습니다.

15장 이진 탐색 트리로 속도 향상

데이터를 특정 순서로 정리할 때, 가장 효율적인 알고리즘은 무엇일까?
정렬 알고리즘은 아무리 빨라도 O(logN)이다. 정렬된 배열에선 삽입과 삭제할 때 O(N)이 걸린다.
해시 테이블은 검색, 삽입, 삭제가 O(1)이지만, 순서를 유지하지 못한다.
순서를 유지하면서 빠른 검색, 삽입, 삭제가 가능한 자료구조하면 어떻게 해야할까?

15.1 트리

트리(tree)는 노드 기반 자료구조이다. 또 다른 노드 기반 자료구조인 연결 리스트는 노드와 다른 한 노드를 연결하는 링크를 포함한다. 트리는 각 노드에 여러 노드의 링크를 포함할 수 있다.

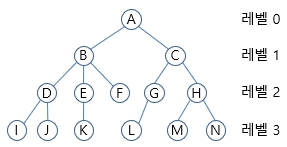
이미지 출처: http://www.ktword.co.kr/test/view/view.php?no=4726

트리의 구성요소

• 루트(Root): 가장 상위 노드 "A"
• 부모: "A"는 "B"와 "C"의 부모
• 자식: "D"와 "E", "F"는 B의 자식
• 조상과 자손: "A"는 나머지 노드의 조상, 나머지 노드는 자손
• 레벨(Level): 트리의 같은 줄(row)
• 프로퍼티(Property): 균형 정도
  • 균형 트리: 모든 노드에서 하위 트리의 노드 개수가 동일
  • 불균형 트리: 모든 노드에서 하위 트리의 노드 개수가 동일하지 않음

15.2 이진 탐색 트리

이진 트리는 각 노드에 자식이 0개나 1개,2개다.
이진 탐색 트리는 다음 규칙이 추가된 트리다.

• 각 노드의 자식은 최대 "왼쪽에"에 하나, "오른쪽"에 하나다.
• 한 노드의 "왼쪽" 자손은 그 노드보다 작은 값만 포함할 수 있다. 오른쪽 자손이 그 노드보다 큰 값만 포함할 수 있다.

코드 구현

class TreeNode {
  constructor(value) {
    this.value = value;
    this.left = null;
    this.right = null;
  }
}

class BinarySearchTree {
  constructor() {
    this.root = null;
  }

  insert(value) {
    const newNode = new TreeNode(value);
    if (!this.root) {
      this.root = newNode;
      return;
    }

    let currentNode = this.root;
    while (currentNode) {
      if (value < currentNode.value) {
        if (!currentNode.left) {
          currentNode.left = newNode;
          return;
        }
        currentNode = currentNode.left;
      } else {
        if (!currentNode.right) {
          currentNode.right = newNode;
          return;
        }
        currentNode = currentNode.right;
      }
    }
  }
}

15.3 검색

찾는 값이 61일 때, 루트 50보다 크기 때문에 오른쪽 하위 노드에서 값을 찾는다.
오른쪽 노드 75보다 작기 때문에 왼쪽 하위 노드 56로 내려가고, 56보다 크기 때문에 오른쪽 하위 노드에 61를 찾을 수 있다. 61를 찾는 데 총 4단계가 걸렸다.

이진 탐색 트리 검색의 효율성

이진 탐색 트리 검색 과정을 보면 각 단계마다 검색할 대상이 남은 노드의 반으로 줄어든다. 따라서 이진 탐색 트리 검색은 O(logN)이다.

log(N) 레벨

이진 트리에 노드가 N개면 레벨이 약 logN개이다.

트리의 모든 노드가 채우져 있다고 가정하자. 하나의 레벨이 추가되면 트리 노드 개수가 대략 두 배로 늘어난다. 레벨 4인 노드에 레벨을 하나 추가하면, 노드 개수가 16개가 추가 되면서 트리 크기가 대략 2배로 늘어난다. log31를 하면 약 5가 된다. 따라서 노드 N개인 트리에서 모든 자리마다 노드를 두려면 logN 레벨이 필요하다.

이진 탐색 트리 검색은 선택한 각 수가 가능한 남은 값 중 반을 제거해서 정렬된 배열의 이진 검색과 효율성이 같다. 그래서 O(logN)의 시간 복잡도를 갖는다.

코드구현

/**
기저조건: 노드가 없으면 None를, 찾고 있던 노드면 노드를 반환

elseif 찾고 있는 값이 현재 노드보다 작으면 왼쪽 노드만 재귀적으로 호출

현재 보다 크면 오른쪽 노드만 재귀적으로 호출
*/

class BinarySearchTree {
  // ... insert 메서드는 생략

  search(value) {
    let currentNode = this.root;
    while (currentNode && currentNode.value !== value) {
      if (value < currentNode.value) {
        currentNode = currentNode.left;
      } else {
        currentNode = currentNode.right;
      }
    }
    return currentNode;
  }
}

15.4 삽입

45를 삽입하려고 할때, 검색 4단계와 삽입 1단계가 걸린다. 즉 logN + 1이므로 O(logN)이다. 정렬된 배열에서의 삽입은 O(N)이 걸린다. 그래서 이진 탐색 트리는 색과 삽입 모두 O(logN)이므로 매우 효율적이다.

코드 구현

/**
현재 노드와 값을 비교해서 값이 작으면 왼쪽, 크면 오른쪽에 삽입해야 한다.
만약 왼쪽 자식이 없으면 그곳에 값이 들어간다. 이 코드가 기저 조건이다.
*/

class BinarySearchTree {
  // ... insert 메서드는 생략

  insert(value) {
    const newNode = new TreeNode(value);
    if (!this.root) {
      this.root = newNode;
      return;
    }

    let currentNode = this.root;
    while (currentNode) {
      if (value < currentNode.value) {
        if (!currentNode.left) {
          currentNode.left = newNode;
          return;
        }
        currentNode = currentNode.left;
      } else {
        if (!currentNode.right) {
          currentNode.right = newNode;
          return;
        }
        currentNode = currentNode.right;
      }
    }
  }
}

삽입 순서

무작위로 정렬된 데이터로 트리를 생성해야 균형 잡힌 트리가 생성된다.
정렬된 데이터는 불균형이 심하고 효율적이지 않다. 정렬된 데이터는 완벽히 선형이라 O(N) 걸린다. 균형 트리일 때만 검색이 대략 O(logN) 걸린다.

15.5 삭제

이진 탐색 트리에서 삭제 알고리즘은 다음과 같은 규칙을 따른다.

• 삭제할 노드에 자식이 없으면 그냥 삭제한다.
• 삭제할 노드에 자식이 하나면 노드를 삭제하고 그 자식을 삭제된 노드가 있던 위치에 넣는다.

class BinarySearchTree {
  // ... insert 메서드는 생략

  delete(value) {
    this.root = this.deleteRec(this.root, value);
  }

  deleteRec(root, value) {
    if (!root) {
      return root;
    }

    if (value < root.value) {
      root.left = this.deleteRec(root.left, value);
    } else if (value > root.value) {
      root.right = this.deleteRec(root.right, value);
    } else {
      // 노드를 찾음
      if (!root.left) {
        return root.right;
      } else if (!root.right) {
        return root.left;
      }

      root.value = this.minValue(root.right);
      root.right = this.deleteRec(root.right, root.value);
    }

    return root;
  }

  minValue(node) {
    let current = node;
    while (current.left) {
      current = current.left;
    }
    return current.value;
  }
}

자식이 둘인 노드 삭제

삭제된 노드 자리에 후속자 노드로 대체한다. 삭제된 노드 다음으로 큰 수가 후속자 노드다.

후속자 노드 찾기

컴퓨터는 후속자 노드를 어떻게 찾을까?
삭제할 노드의 오른쪽 하위 트리에서 가장 작은 값을 가진 노드가 후속자 노드가 된다.

이진 탐색 트리 삭제의 효율성

O(logN)이다. 삭제에는 검색 한 번과 연결이 끊긴 자식을 처리하느 단계가 추가로 필요하기 때문이다.

15.6 이진 탐색 트리 다뤄보기

이진 탐색 트리는 데이터 삽입 삭제가 정렬된 배열보다 훨씬 빠르기 때문에 데이터를 자주 수정하는 경우 효율적이다.

15.7 이진 탐색 트리 순회

모든 노드를 방문하는 과정을 자료 구조 순회라 부른다.
각 제목을 알파벳 순으로 출력하는 것은 중위 순회이다.

요약

이진 탐색 트리는 데이터 구조에서 검색, 삽입, 삭제를 효율적으로 수행할 수 있는 구조로, 특히 데이터를 자주 수정해야 하는 경우에 매우 유리하다. 이진 탐색 트리의 주요 특성과 동작을 정리하면 다음과 같다.

1. 이진 탐색 트리의 특성

   • 각 노드의 자식은 최대 두 개.
   • 왼쪽 자식 노드는 부모 노드보다 작고, 오른쪽 자식 노드는 부모 노드보다 크다.

2. 시간 복잡도

   • 검색, 삽입, 삭제: 모두 평균적으로 O(logN)의 시간 복잡도를 가지며, 이는 트리가 균형을 이룰 때 성립한다.
   • 최악의 경우, 즉 트리가 한쪽으로 치우친 경우(예: 정렬된 데이터를 삽입할 경우), 시간 복잡도는 O(N)까지 증가할 수 있다.

3. 삽입과 삭제

   • 삽입: 새 노드를 적절한 위치에 삽입하여 트리 구조를 유지한다.
   • 삭제: 노드의 자식 수에 따라 다른 방법으로 처리된다. 자식이 하나인 경우 그 자식을 삭제된 노드의 위치로 이동시키고, 자식이 둘인 경우 후속자 노드를 찾아 대체한다.

4. 트리 순회

   • 중위 순회(Inorder Traversal): 왼쪽 자식, 현재 노드, 오른쪽 자식 순으로 방문하며, 이는 이진 탐색 트리에서 데이터를 정렬된 순서로 출력하는데 유용하다.

이진 탐색 트리는 정렬된 배열보다 삽입과 삭제가 빠르고, 해시 테이블보다 순서를 유지할 수 있다는 장점이 있다. 다만, 균형 잡힌 트리를 유지하기 위해서는 균형 트리 알고리즘(예: AVL 트리, 레드-블랙 트리 등)을 적용하는 것이 좋다.

// 이진 탐색 트리 구현 예시
class TreeNode {
  constructor(value) {
    this.value = value;
    this.left = null;
    this.right = null;
  }
}

class BinarySearchTree {
  constructor() {
    this.root = null;
  }

  insert(value) {
    const newNode = new TreeNode(value);
    if (!this.root) {
      this.root = newNode;
      return;
    }

    let currentNode = this.root;
    while (currentNode) {
      if (value < currentNode.value) {
        if (!currentNode.left) {
          currentNode.left = newNode;
          return;
        }
        currentNode = currentNode.left;
      } else {
        if (!currentNode.right) {
          currentNode.right = newNode;
          return;
        }
        currentNode = currentNode.right;
      }
    }
  }

  search(value) {
    let currentNode = this.root;
    while (currentNode && currentNode.value !== value) {
      if (value < currentNode.value) {
        currentNode = currentNode.left;
      } else {
        currentNode = currentNode.right;
      }
    }
    return currentNode;
  }

  delete(value) {
    this.root = this.deleteRec(this.root, value);
  }

  deleteRec(root, value) {
    if (!root) {
      return root;
    }

    if (value < root.value) {
      root.left = this.deleteRec(root.left, value);
    } else if (value > root.value) {
      root.right = this.deleteRec(root.right, value);
    } else {
      if (!root.left) {
        return root.right;
      } else if (!root.right) {
        return root.left;
      }

      root.value = this.minValue(root.right);
      root.right = this.deleteRec(root.right, root.value);
    }

    return root;
  }

  minValue(node) {
    let current = node;
    while (current.left) {
      current = current.left;
    }
    return current.value;
  }

  inorderTraversal(node = this.root, result = []) {
    if (node) {
      this.inorderTraversal(node.left, result);
      result.push(node.value);
      this.inorderTraversal(node.right, result);
    }
    return result;
  }
}

이 코드는 이진 탐색 트리의 기본적인 기능을 포함하고 있으며, 이를 통해 효율적인 데이터 검색, 삽입, 삭제, 그리고 트리 순회를 수행할 수 있다.