Find Center of Star Graph & Find if Path Exists in Graph

Guk's.velog·2024년 6월 12일

99클럽 DFS Graph TIL 개발자 코딩테스트 항해99

코딩테스트

목록 보기

13/22

문제

Find Center of Star Graph

배열을 주어주고 Graph와 같은 형태로 만들어지는 상황에서 중앙 노드에 해당하는 값을 찾는 문제이다. 조건중에 모든 노드는 중앙 노드와 연결된다고 되어있다.

접근 방법

처음에는 해당 문제를 일일히 탐색해야하는건가 싶었다. 근데 곰곰이 생각해 보아도 전체를 순회하는건 원하는 접근 방법이 아니었다. 그래서 규칙을 찾아보았다.

해결 방법

var findCenter = function(edges) {
    const [[a, b], [c, d]] = edges;
    return a === c || b === c ? c : d;
};

의외로 단순하다. 조건에서 모든 노드가 중앙에 연결되어있기 때문에 사실상 두개의 노드만 비교해서 값이 중복되는 수가 있을경우 해당 수를 return하면 된다.

진짜 Graph다운(?) 문제를 풀어보기로 한다.

문제

Find if Path Exists in Graph

Graph형태의 Node를 주어지고 시작점과 목적지의 연결여부를 확인하는 문제이다.

접근 방법

과거 강의에서 배웠던 Graph와 DFS, BFS 등을 떠올려서 더듬더듬 구현해보았으나.. 역시 오랜만이라서 쉽지는 않았다. 해서 DFS의 원리를 먼저 파악해본다.

DFS(Depth-First Search)란?

깊이 우선 탐색이라고도 부르며, 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘이다. 스택 자료구조(혹은 재귀 함수)를 이용한다.

탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
스택의 최상단 노드에 방문하지 않은 인접한 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문 처리한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
더 이상 2번 과정을 수행할 수 없을 때까지 반복한다.

그래프 탐색 순서는 다음과 같이 진행된다.

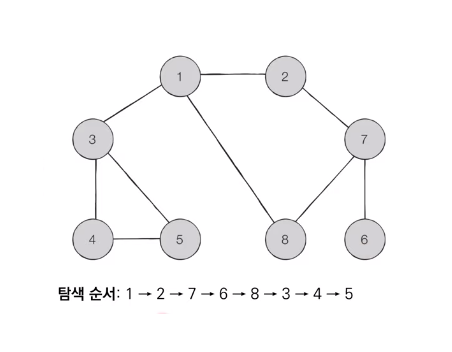
코드

var validPath = function(n, edges, source, destination) {
    let adj = [];
    let vis = new Array(n).fill(false);

    for(let i = 0 ;i < n ; i++){
        adj.push([]);
    }

    for(let i = 0 ; i < edges.length ; i++){ // 인접 리스트 생성
        adj[edges[i][0]].push(edges[i][1]);
        adj[edges[i][1]].push(edges[i][0]);
    }

    for(let i = 0 ; i < n ; i++){ // 컴포넌트가 항상 연결되어 있지 않기 때문에 이 반복문이 필요함
        if(!vis[i] && i == source){ // 소스 노드를 찾으면 DFS 시작
            let f = dfs(i); // 소스 노드에서 DFS 수행
            if(f){
                return true; // 유효한 경로가 발견되면 true 반환
            }
        }
    }

    function dfs(node){
        vis[node] = true; // 현재 노드를 방문한 것으로 표시

        if(node == destination){
            return true; // 노드 자체가 목적지인 경우
        }

        for(let n of adj[node]){
        
            if(vis[n] && node == destination){ // 목적지를 찾은 경우
                return true;
            }
            // 이웃 노드를 방문하지 않은 경우 재귀적으로 DFS 호출
            if(!vis[n] && dfs(n)){
                return true; // 유효한 경로가 발견되면 true 반환
            }
        }

        return false; // 현재 노드에서 유효한 경로가 발견되지 않으면 false 반환
    }

    return false; // 그래프 전체를 탐색한 후에도 경로가 발견되지 않으면 false 반환

};