DFS와 조합의 경우수(메모)

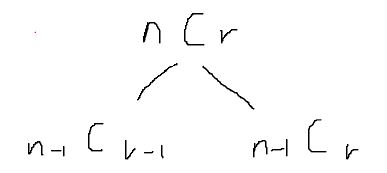
문제

조합수를 구하는 공식 중 가장 널리 알려진 방식은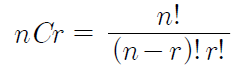
이지만, 이 문제에서는 DFS 연습을 위해 아래와 같은 공식을 사용한다.

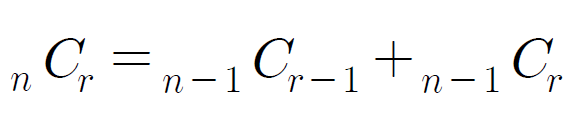
예시

n	r	result
5	3	10
33	19	818809200

조건: 3<= n <= 33 , 0 <= r <= n

풀이

• nCr 이 n-1Cr-1 + n-1Cr 과 같으므로, n개 중 r개를 뽑는 DFS(n,r) 함수를 작성하고, DFS 함수 내부에서 다시 DFS(n-1,r-1) 과 DFS(n-1,r) 을 호출하면서 경우의 수들을 더해나가면 된다.

	const DFS(n,r) = () => {
      		return DFS(n-1, r-1) + DFS(n-1, r);
    	}

• 위 DFS 함수의 종료 조건은 n===r 일 때 (5C5는 언제나 1이므로), 또는 r === 0 일 때 (nC0 은 언제나 1이므로) 이다.

	const DFS(n,r) => () => {
		if(n === r || r === 0) return 1;
      	else return DFS(n-1, r-1) + DFS(n-1, r);
    }

• 여기까지만 해도 답을 구할 수는 있지만, 만약 n === 33 , r===19 과 같이 결과값이 조금이라도 큰 수를 구할 때는 문제가 생긴다.
  

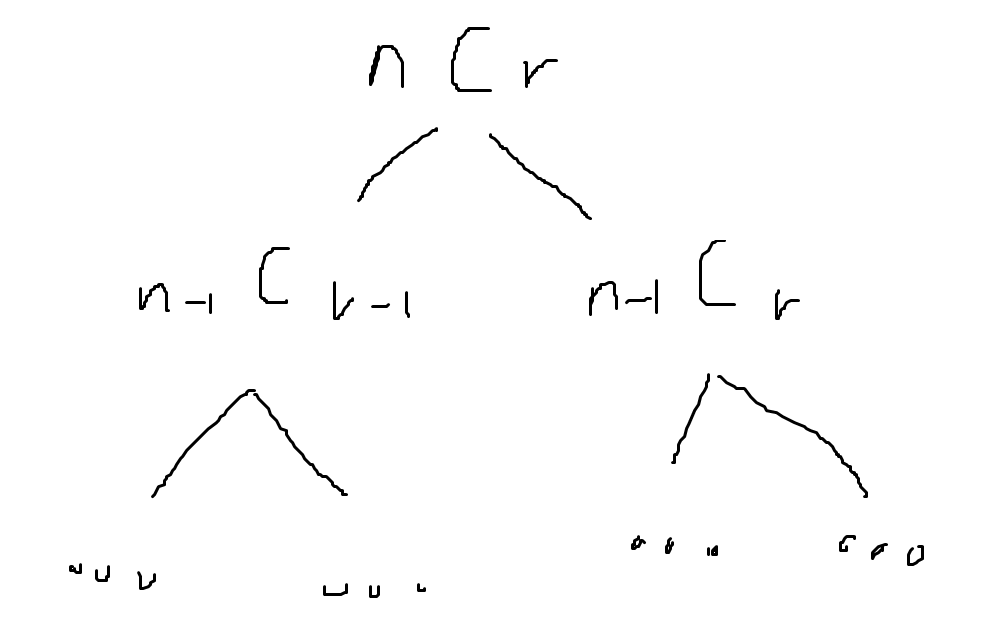
  위 그림에서 n과 r에 각각 33, 19 를 대입해보면, 트리의 가지가 셀 수 없이 많이 생기리란 걸 짐작할 수 있다.

• 하지만 만약에 가지를 아래로 뻗어 나가면서 이전에 계산했던 값을 저장해둔다면 어떨까?
  

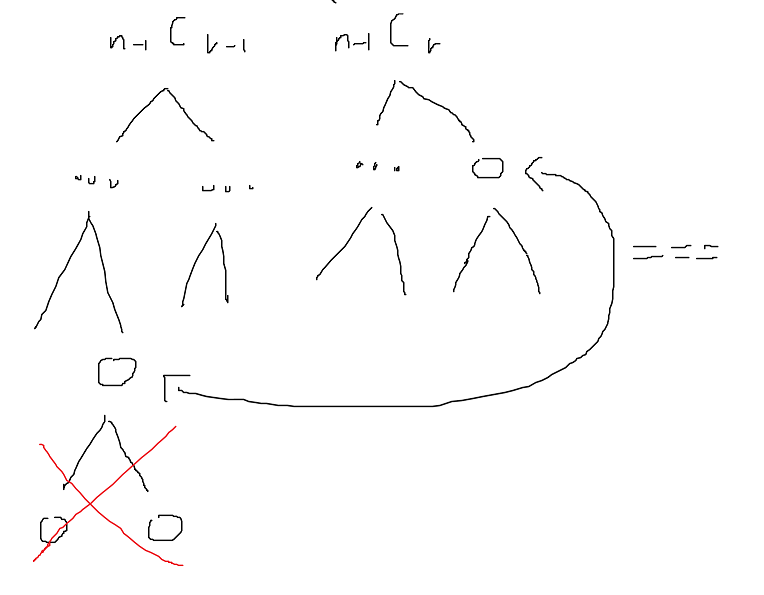
  아래쪽 노드에서 사용할 n, r 이 이전에 이미 계산해봤던 n, r 이라면 굳이 아래로 노드를 더 뻗어나갈 필요가 없다!

• 이러한 기술을 메모이제이션 이라고 하는데, 이전에 연산했던 값을 따로 저장해서 불필요한 재연산을 막는 방법이다.

	const memo = Array.from({ length: 35 }, () =>
		Array.from({ length: 35 }, () => 0)
	);

• 문제에서 n 의 범위를 33까지 정해줬으므로, 조금 여유있게 35의 길이를 갖는 2차원 빈 배열을 생성했다. 2차원 배열인 이유는 n과 r 두 개의 인덱스가 변수로 작용하기 때문이다.

• 이제 위에서 작성한 DFS 함수에 메모이제이션을 적용해 불필요한 재연산을 막아보자.

	const DFS = (n, r) => {
		if (memo[n][r]) return memo[n][r];
		if (n === r || r === 0) return 1;
		else {
			return (memo[n][r] = DFS(n - 1, r - 1) + DFS(n - 1, r));
		}
	};

DFS 함수가 실행되었을 때, memo[n][r] 에 특정 값이 있으면 이미 전에 연산했던 nCr 이라는 뜻이므로, DFS (n,r) === memo[n][r] 이 된다.

회고

• 이전에도 풀어봤던 문제지만, 메모이제이션은 다시 한번 더 정리를 해야 할 필요성을 느꼈다. 컴퓨터가 쓸데없는 연산을 하지 않게 해준 다는 점에서 참 매력적인 것 같다.

코드

const solution = (n, r) => {
	let answer = 0;
	const memo = Array.from({ length: 35 }, () =>
		Array.from({ length: 35 }, () => 0)
	);

	const DFS = (n, r) => {
		if (memo[n][r]) return memo[n][r];
		if (n === r || r === 0) return 1;
		else {
			return (memo[n][r] = DFS(n - 1, r - 1) + DFS(n - 1, r));
		}
	};

	DFS(n, r);
	answer = memo[n][r];
	return answer;
};