

1. ANOVA
- 2개 이상 그룹의 평균에 차이가 있는지 확인하는 방법이다.
- F-value를 통해 그룹 간의 차이를 살핀다.
- 데이터가 서로 독립인지 / 등분산인지 / 정규성을 띄고 있는지 확인이 필요핟.
F- value = 그룹 간의 차이 / 그룹 내의 차이
- F-value가 높다는 건 다른 그룹 간의 차이는 크고, 그룹 내의 차이는 작다는 뜻이다.
- 즉, 다른 그룹끼리의 분포가 다르다고 추정할 수 있다.
2. 큰 수의 법칙
- sampling한 데이터의 규모가 커질 수록 sample의 통계치는 모집단의 모수와 같아진다.
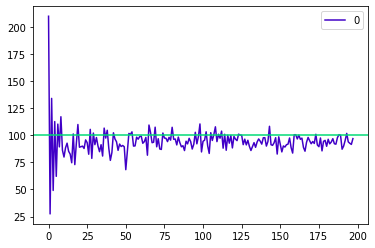
3. 중심극한정리
- 모집단에 대해 sampling을 반복할 수록, sample의 평균은 정규분포에 근사한 형태가 된다.
- 모집단이 어떤 형태를 모르더라도 모집단을 추정할 수 있는 근거가 된다.
4. 신뢰구간
- 신뢰도 95%는 표본을 100번 뽑았을 때 95번은 신뢰구간에 모집단의 평균이 포함될 것이라는 의미이다.
5. P-value
- 통상 설정하는 유의수준 5%는 2종 오류의 크기를 의미한다.
- 유의수준을 5%로 고정하는 순간 의미 없는 표본 중에서 5%는 유의성 검정에서 유의미한 것으로 판단할 수 있기 때문이다.
- 즉, 데이터에서 유의미성을 판단하기 위해 어쩔 수 없이 유의수준만큼의 틀릴 가능성을 감당하는 것이다. 1종 오류를 줄이기 위해 2종 오류를 어느정도 허용한다는 의미로 이해할 수 있다.
- 유의수준을 1% 정도로 낮추면 차이가 있는 데이터에 차이를 발견하기 어려워지는데, 이는 1종 오류를 범할 가능성이 크다는 것을 의미한다.
