1. 자료구조와 알고리즘
- 일상 생활에서 자료를 정리하고 조직화하는 이유는?
- 자료구조와 알고리즘의 관계
자료구조는 알고리즘 과목의 직전 단계이기도 하고, 그 자체로 여러 알고리즘을 포함
자료구조
컴퓨터에서 자료를 정리하고 조직화하는 다양한 구조
선형 자료구조
항목들을 순서적으로 나열하여 저장하는 창고
항목 접근 방법에 따라 다시 세분화
- 리스트 : 가장 자유로운 선형 자료구조
- 스택, 큐, 덱 : 항목의 접근이 전단이나 후단으로 제한
비선형 자료구조
항목들이 보다 복잡한 연결관계
- 트리 : 회사의 조직도나 컴퓨터의 폴더와 같은 계층 구조
ㄴ힙 트리는 우선순위 큐
ㄴ이진 탐색트리나 AVL트리 : 탐색을 위한 트리 구조 - 그래프 : 가장 복잡한 연결 관계를 표현
다양한 문제를 해결하기 위한 기본 구조로 사용된다.
알고리즘
컴퓨터로 문제를 풀기 위한 단계적인 절차 ex)사전에서 단어 찾기
알고리즘의 조건
- 입력 : 0개 이상의 입력이 존재하여야 한다.
- 출력 : 1개 이상의 출력이 존재하여야 한다.
- 명백성 : 각 명령어의 의미는 모호하지 않고 명확해야한다.
- 유한성 : 한정된 수의 단계 후에는 반드시 종료 되어야 한다.
- 유효성 : 각 명령어들은 실행 가능한 연산이어야 한다.
알고리즘의 기술 방법
- 자연어 : 읽기 쉬움. 단어들을 정확하게 정의하지 않으면 의미 모호.
- 흐름도 : 직관적. 이해하기 쉬움. 복잡한 알고리즘→상당히 복잡!(대형프로그램에서 사용불편)
- 유사코드
프로그램을 구현할 때의 여러가지 문제들을 감출 수 있음 ㅇ
알고리즘의 핵심적인 내용에만 집중 가능 - 특정 언어
알고리즘의 가장 정확한 기술 가능
구현시의 사항들이 알고리즘의 핵심적인 내용들의 이해를 방해
파이썬: C나 자바보다 훨씬 간결한 표현 가능
2. 추상자료형
추상자료형(Abstract Data Type, ADT)
프로그래머가 추상적으로 정의한 자료형
- 데이터 타입을 추상적으로 정의한 것
ㄴ 데이터나 연산이 무엇인가를 정의함
ㄴ 데이터나 연산을 어떻게 구현할 것인지는 정의하지 않음 - 시스템의 정말 핵심적인 구조나 동작에만 집중
예 Bag의 추상 자료형

bag = []
def contains(bag,e):
return e in bag #boolean
def insert(bag,e):
bag.append(e)
def remove(bag,e):
bag.remove(e)
def count(bag,e):
return bag.len()
insert(bag,"휴대폰")
insert(bag,"지갑")
insert(bag,"손수건")
insert(bag,"빗")
insert(bag,"자료구조")
insert(bag,"야구공")
print(f"mybag: {bag}")
insert(bag,"빗") #중복
remove(bag,"손수건")
print(f"mybag: {bag}")
contains(bag,"빗")3. 알고리즘의 성능 분석
1. 실행 시간을 측정하는 방법
- 두개의 알고리즘의 실제실행시간을 측정하는것
- 실제로 구현하는 것이 필요
- 동일한 하드웨어를 사용하여야 함
import time
my_bag = []
start = time.time()
#...
insert(bag,"휴대폰")
insert(bag,"지갑")
insert(bag,"손수건")
insert(bag,"빗")
insert(bag,"자료구조")
insert(bag,"야구공")
print(f"mybag: {bag}")
insert(bag,"빗") #중복
remove(bag,"손수건")
print(f"mybag: {bag}")
print(contains(bag,"빗"))
#
end = time.time()
print(f"실행시간 = {end - start}")2. 알고리즘의 복잡도를 분석하는 방법
- 직접 구현하지 않고서도 수행 시간을 분석하는 것
- 알고리즘이 수행하는 연산의 횟수를 측정하여 비교
- 일반적으로 연산의 횟수는 n의 함수
시간복잡도분석 : 수행시간분석
– 산술, 대입, 비교, 이동의 기본적인 연산 고려
– 알고리즘 수행에 필요한 연산의 개수를 계산
– 입력의 개수 n에 대한 함수->시간복잡도 함수, T(n)
- 빅오표기법: 대부분 채택되는 표기법
ex: 등교 시간 분석
• 집을 나와서 지하철역까지는 5분, 지하철을 타면 학교 까지 30분, 강의실까지는 걸어서 10분 걸린다
• 최선경우Ω(n^2): 수행시간이 가장 빠른 경우
집을 나와서 5분 후 지하철역에 도착하고, 운이 좋게 바로 열차를 탄 경우를 의미한다. 따라서 최선경우 시간은 5 + 20 + 10 = 35분
• 최악경우O(n^2): 수행시간이 가장 늦은 경우 가장 널리 사용된다.
열차에 승차하려는 순간, 열차의 문이 닫혀 서 다음 열차를 기다려야 하고 다음 열차가 10분 후에 도착한다면, 최악경우는 5 + 10 + 20 + 10 = 45분
• 평균경우θ(n^2): 대략 최악과 최선의 중간이라고 가정했을 때, 40분이 된다.
공간복잡도분석:수행시 필요로하는 메모리공간분석
4. 시간 복잡도 분석 : 순환 알고리즘
순환알고리즘이란
알고리즘이나 함수가 수행도중에 자기자신을 다시 호출하여 문제를 해결하는 기법
정의자체가 순환적으로 되어 있는 경우에 적합
팩토리얼 계산
def factorial(n):
if n == 1:
return 1
else :
return n * factorial(n-1) 함수안에 함수를 배치하면 순환 함수이다.
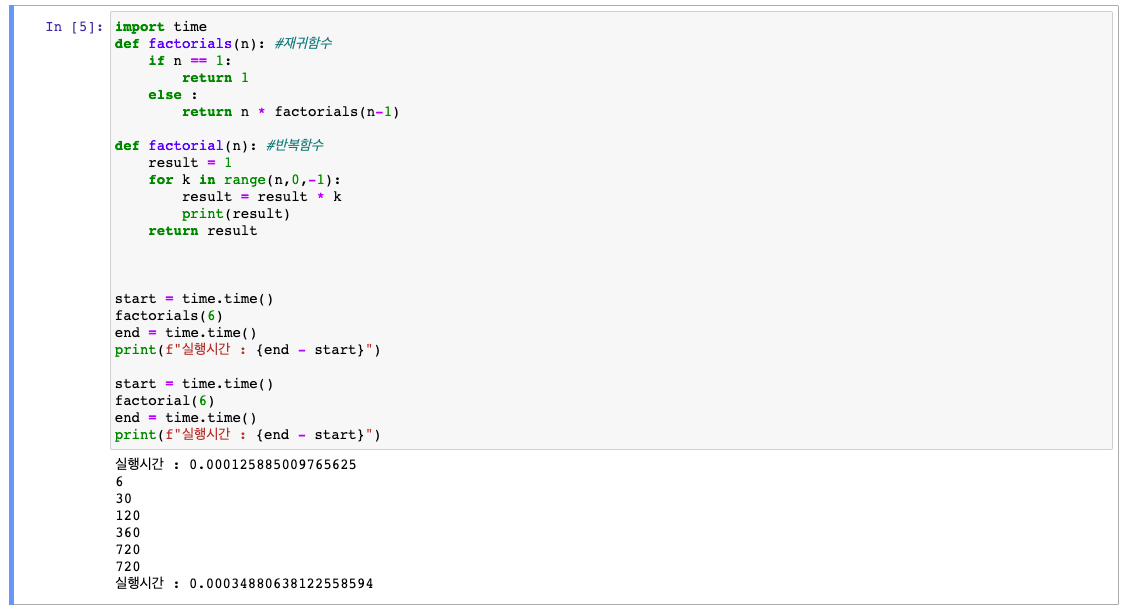
거듭제곱
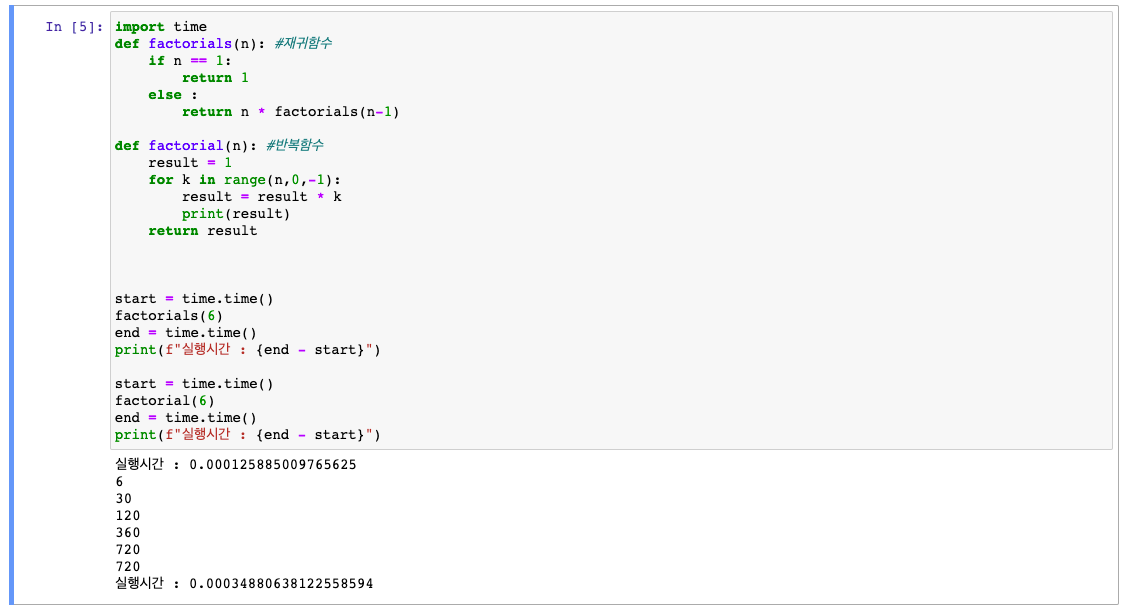
피보나치 수열(반복이 우세)

처음에 작은 값을 넣었을때는 순환이 내용과 다르게 더빨랐지만 큰수를 넣었더니 차이가 확연히 난다.
하노이의 탑
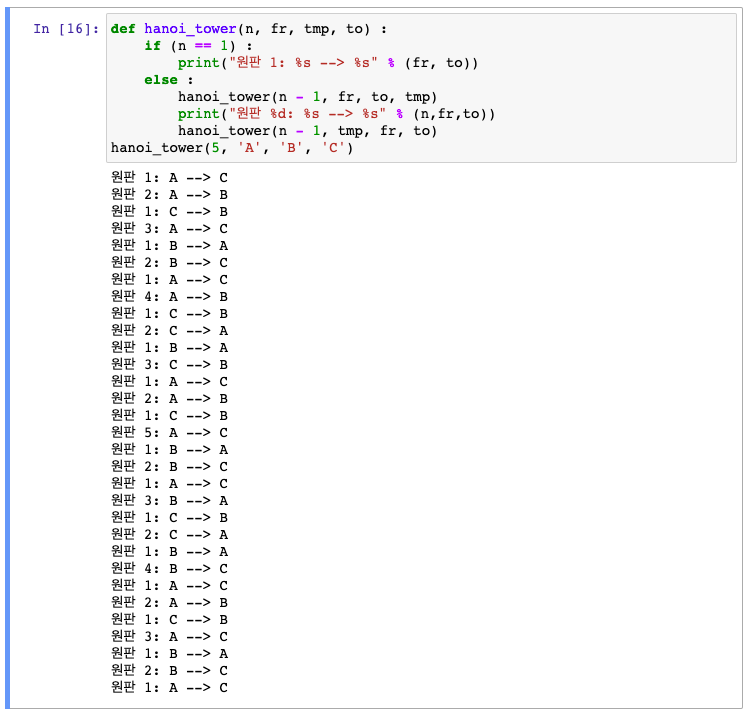
반복함수는 만들어봐야할 것 같다.
