정의
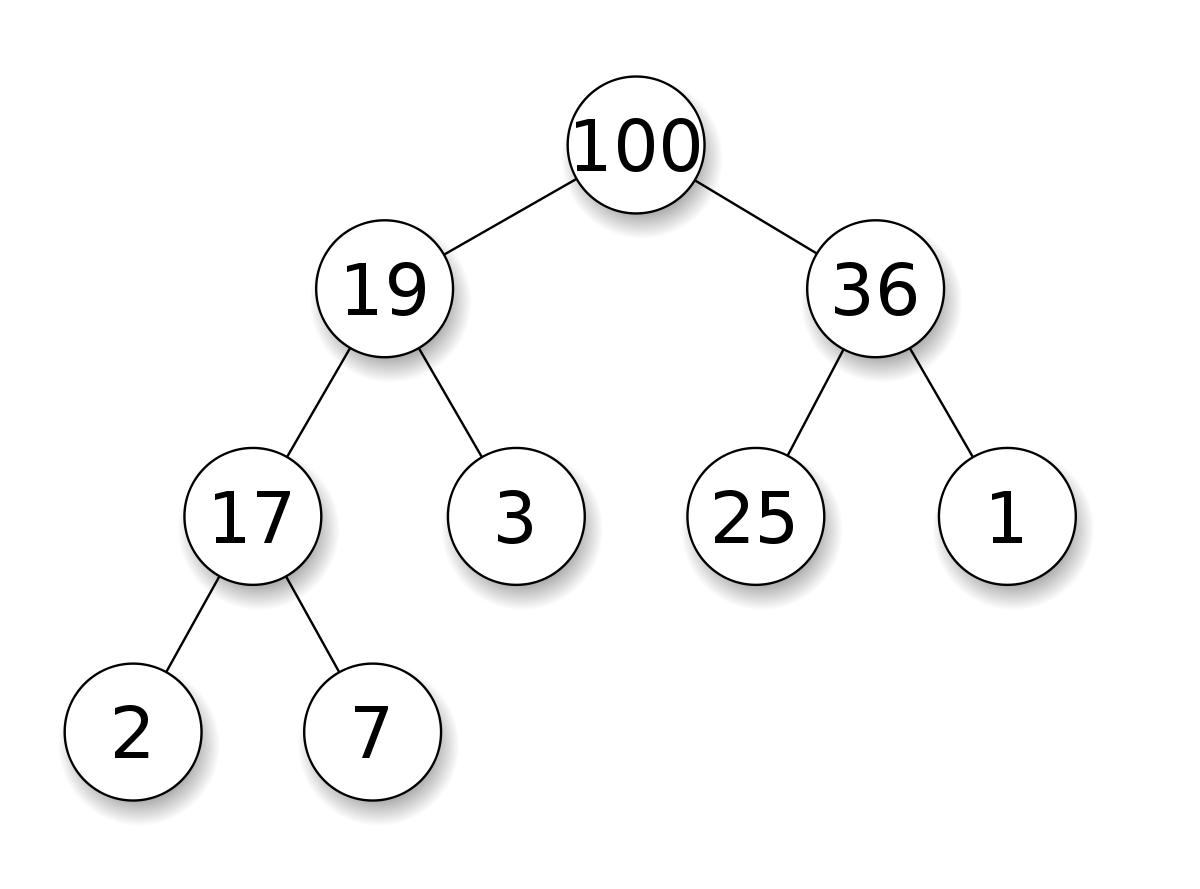
힙은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리를 기본으로 한 자료구조이다.
특징
부모 노드와 자식 노드 간에 대소 관계가 성립한다.
- 최대 힙 : 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 힙
- 최소 힙 : 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 힙
가장 높은(낮은) 우선순위를 가지는 노드가 항상 root 노드에 위치하게 되며, 이 특징을 이용해 우선 순위 큐와 같은 자료형을 구현할 수 있다.
힙을 배열로 표현하게 되면 i번째 노드의 왼쪽 자식 노드의 위치는 2i이며, 오른쪽 자식의 노드는 2i+1이며, i번째 노드의 부모 노드의 위치는 i/2가 된다.
사용 및 연산
python document : heapq
파이썬에서 힙은 heapq를 이용해 구현한다.
비어 있는 리스트를 선언한 뒤, heapify()를 통해 heap을 구현한다.
import heapq
heap = []
heapq.heapify(heap)heappush(heap, item)
heap 성질을 유지하면서 heap에 item을 추가한다.
heapq.heappush(heap, 1)
heapq.heappush(heap, 2)
heapq.heappush(heap, 3)
print(heap)
>>> [1,2,3]heappop(heap)
heap에서 최솟값을 pop해서 return한다. heap이 비어 있다면 IndexError를 발생시킨다. 즉, heapq는 자동으로 최소 힙을 생성하는 것을 알 수 있다.
heapq.heappop(heap)
>>> 1두 연산 모두 O(logn)의 시간 복잡도를 갖는다.
YOU ARE BREATHTAKING