하노이의 탑 정리

하노이의 탑 정리

하노이의 탑은 알고리즘 초급 수업에서 재귀 입문으로 이 문제를 많이 다룬다고 한다.하노이의 탑의 조건은 다음과 같다.

1. 한번에 움직일수 있는 원반의 기둥은 위에 놓인 원반 하나 뿐이다.
2. 어떤 원반 위에 그보다 더 큰 원반을 쌓을수 없다.

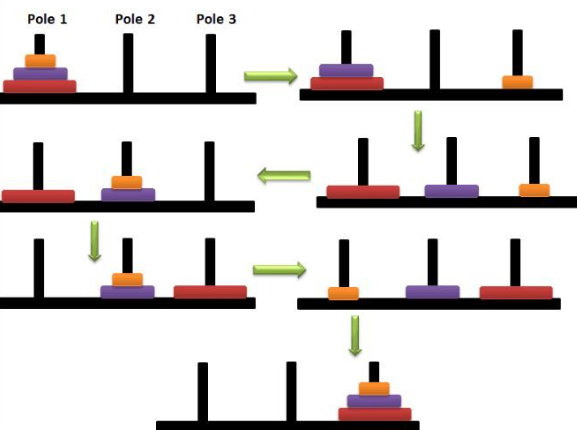
사진 출처 : https://brunch.co.kr/@younggiseo/139

위 사진처럼 조건애 맞게 하나씩 옮겨서 다른위치로 탑을 옮기는 것이다.

아이디어

하노이의 탑에서 모두 옮기지 못하니 3개의 고리? 중에 시작지점, 도착지점, 경유지점을 이용한다.

큰 원판 이외의 원판들을 모두 경유 지점으로 옮기고 목표지점으로 큰 원판을 옮기고 다시 작은 원판들을 목표지점으로 옮기면 된다.

함수 호출로 하기 때문에 큰것을 옮기고 작은것들을 다시 옮기는데 재귀함수 호출로 그안에서 작은것들중에서 작은것들을 옮기고 그중에서도 큰것을 옮기고 이런식으로 재귀 호출로 인하여 모든 출력이 나타나게 될것임

# 하노이 탑 알고리즘
def hansol(n, start, end):
    def move(start, end):
        print(f'{start} -> {end}')
    def hansol_move(n, start_point, target_point, middle_point):
        if n == 1:
            move(start_point, target_point)
        else:
            hansol_move(n-1, start_point,middle_point,target_point)
            move(start_point, target_point)
            hansol_move(n-1, middle_point, target_point, start_point)
    hansol_move(n,start,end,'C')

A = 'A'
B = 'B'

hansol(3, A,B)

# 결과
A -> B
A -> C
B -> C
A -> B
C -> A
C -> B
A -> B

알고리즘 순서도 정리

hansol(3,A,B)
hansol_move(3,A,B,C)
//else문 실행
hansol_move(2,A,C,B)
move(A,B)
hansol_move(2,C,B,A)
// 위순서대로 실행될것임


hansol_move(2,A,C,B) 
 hansol_move(1,A,B,C)
  move(A,B)
 move(A,C)
 hansol_move(1,B,A,C)
  move(B,C)
move(A,B)
hansol_move(2,C,B,A)
 hansol_move(1,C,A,B)
  move(C,A)
 move(C,B)
 hansol_move(1,A,B,C)
  move(A,B)
함수 종료

이렇게 정리하고 보면 되게 간단한 코드이고 이제야 이해가 조금 되긴 하지만 막상 무작정 풀려고 하니 손도 못댈 정도였음.. 천천히 차근차근 찾아보며 이해하려고 하다보니 조금씩 이해가 되었음.
프로그래밍을 할때는 무작정 하는것이 아닌 어떻게 할지 생각하고 하는것이 중요하다고 생각해볼수 있는 계기가 되었음.