[백준] 1520번 내리막길

백준 1520번 - 내리막길

문제

여행을 떠난 세준이는 지도를 하나 구하였다. 이 지도는 아래 그림과 같이 직사각형 모양이며 여러 칸으로 나뉘어져 있다. 한 칸은 한 지점을 나타내는데 각 칸에는 그 지점의 높이가 쓰여 있으며, 각 지점 사이의 이동은 지도에서 상하좌우 이웃한 곳끼리만 가능하다.

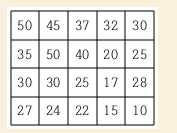
현재 제일 왼쪽 위 칸이 나타내는 지점에 있는 세준이는 제일 오른쪽 아래 칸이 나타내는 지점으로 가려고 한다. 그런데 가능한 힘을 적게 들이고 싶어 항상 높이가 더 낮은 지점으로만 이동하여 목표 지점까지 가고자 한다. 위와 같은 지도에서는 다음과 같은 세 가지 경로가 가능하다.

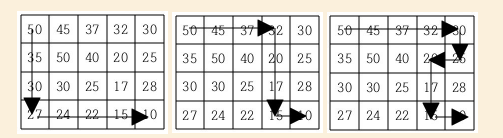
지도가 주어질 때 이와 같이 제일 왼쪽 위 지점에서 출발하여 제일 오른쪽 아래 지점까지 항상 내리막길로만 이동하는 경로의 개수를 구하는 프로그램을 작성하시오.

접근방법

DP + DFS를 이용해서 풀었다.

즉 다시 말해 이미 [height, width]로 탐색을 했던 길이라면 탐색하지 않고 값을 반환하여 사용한다.

처음엔 BFS로 접근하였는데, 메모리초과로 실패
따라서 DP를 이용해야 한다고 생각함.
처음에는 return DP[height][width]로 하려했는데 그럴 경우 위로가는 경우, 좌로 가는 경우에 놓치는 경우가 생겼다.

따라서 DP[y][x]를 y,x에서 height, width로 가는 경우의수로 정의하여 1,1로 경우의 수가 수렴하는 방식으로 접근하여 풀이하였다.

코드

class IO1520 {
    private val br = System.`in`.bufferedReader()
    private val bw = System.out.bufferedWriter()

    fun getHeightAndWidth() = br.readLine().split(" ").map { it.toInt() }
    fun getRow() = br.readLine().split(" ").map{ it.toInt() }
    fun flush() = bw.flush()
    fun close() = bw.close()
    fun write(message: String) = bw.write(message)
}

fun main() {
    val io = IO1520()
    val (height, width) = io.getHeightAndWidth()

    val dx = arrayOf(-1,1,0,0)
    val dy = arrayOf(0,0,-1,1)

    val graph = Array(height) { Array (width) { -1 } }
    val dp = Array(height) { Array (width) { -1 } }

    repeat(height) {
        io.getRow().forEachIndexed { idx, h ->
            graph[it][idx] = h
        }
    }

    fun dfs(y: Int, x: Int): Int {
        if ( y == height -1 && x == width -1) {
            return 1
        }
        if (dp[y][x] != -1) return dp[y][x]
        else dp[y][x] = 0
        dy.forEachIndexed { idx, cy ->
            val nx = dx[idx] + x
            val ny = cy + y
            if (nx in 0 until width && ny in 0 until height && graph[y][x] > graph[ny][nx]) {
                dp[y][x] += dfs(ny, nx)
            }
        }
        return dp[y][x]
    }


    io.write(dfs(0,0).toString())
    io.flush()
    io.close()
}