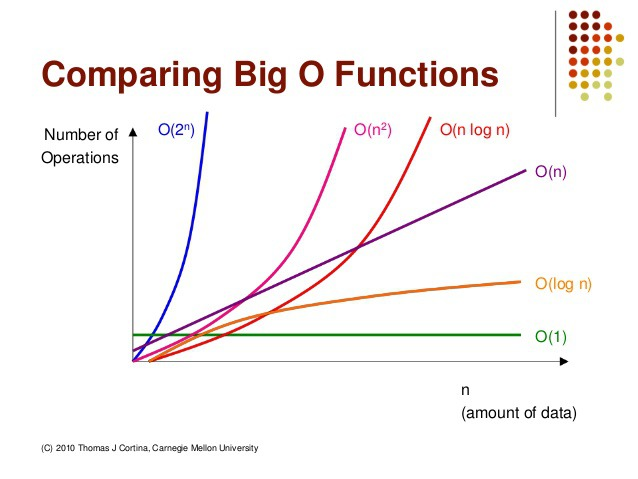
빅 오 표기법(Big-O Notation)이란?
시간 복잡도를 쉽게 소통할 목적으로 자료 구조와 알고리즘의 효율성을 간결하고 일관된 언어로 설명하기 위해 수학적 개념을 차용한 것.
상한선 기준으로 표기한다. 즉, 최악의 경우 몇 단계가 필요한지를 표기하는 방법이다.
빅 오 표기법은 그 값이 클수록, 그리고 그래프가 위로 향할수록 비효율적임을 의미한다.
시간 단위가 아닌 알고리즘에 필요한 단계 수만을 고려한다.
이미지 출처:https://noahlogs.tistory.com/27
O(1)
"빅 오 1" 혹은 "차수 1"이라고 부른다.
데이터 크기에 상관없이 알고리즘에 필요한 단계 수는 한 단계로 동일해 "상수시간(constant time)"이라고도 부른다.
어떤 알고리즘 보다도 효율적임을 뜻한다.
O(1)이 쓰이는 경우:
- 배열 읽기
- 배열 끝의 삽입과 삭제
- 스택에서의 push, pop
O(N)
"오 N"이라고 한다.
데이터가 하나씩 추가될 때마다 알고리즘이 한 단계씩 더 걸리기 때문에 "선형시간(linear time)"이라고도 부른다.
선형 검색의 효율성을 표현하는 데에 쓰인다. 한 번에 한 셀씩 확인해서 배열에서 특정 값을 검색하는 선형 검색의 경우, 최대 배열의 원소 수만큼의 단계가 필요하다.
데이터 원소가 N개 있으면 알고리즘에서 최대 N단계가 걸린다는 의미가 된다.
O(N)이 쓰이는 경우:
- for문
- 배열에서 특정 원소 검색
O(log N)
"오 로그 N"이라고 한다.
이진 검색의 시간 복잡도를 의미하며, 이 유형의 알고리즘을 로그 시간(log time)의 시간 복잡도라고 말한다.
데이터가 두 배로 증가할 때마다 딱 한 단계씩 늘어나는 알고리즘을 설명하는 방법이다.
다시 말하면 원소가 하나가 될 때까지 데이터 원소를 계속해서 반으로 줄이는 만큼의 단계 수가 걸린다는 의미이다.
O(log N)이 쓰이는 경우:
- 이진 트리
빅 오메가(Big-Ω) 표기법 / 빅 세타(Big-θ) 표기법
빅 오 표기법 이외에도 빅 오메가(Big-Ω), 빅 세타(Big-θ) 표기법 등이 있다.
- 빅 오메가(Big-Ω) 표기법: 최선의 경우를 의미한다. 즉, 최소한 몇 단계가 걸리는지를 표기하는 방법이다.
- 빅 세타(Big-θ) 표기법: 평균적인 상황의 경우를 의미한다. 보통 빅 오(Big-O)와 빅 오메가(Big-Ω)의 공통부분이 되며, 빅 세타로 표현할 수 없는 경우도 존재한다.
링크드 리스트(Linked List)란?
연결 리스트라고도 한다. 배열과 마찬가지로 항목의 리스트를 표현하는 자료구조다.
그러나 배열이 나란히 이어진 메모리 셀 묶음인 반면, 링크드 리스트는 서로 인접하지 않은 메모리 셀 묶음으로 이루어진다.
링크드 리스트를 이루고 있는 노드(Node)에는 두개의 셀이 있는데, 첫 번째 셀에는 실제 데이터가 들어 있고, 두 번째 셀에는 다음 노드의 시작 메모리 주소를 뜻하는 링크가 들어 있다.
그리고 마지막 노드의 링크는 링크드 리스트가 끝나므로 Null이 된다.
연속배열(Array) vs. 링크드리스트(Linked List)
검색
검색에서 배열과 링크드 리스트의 효율성은 같다.
배열이든 링크드 리스트든 프로그램은 검색하고 있는 값을 찾을 때까지 첫 번째 셀부터 시작해서 모든 셀을 하나씩 확인해야 하기 때문이다.
최악의 시나리오라면 O(N)단계가 걸린다.
삽입
1. 0번째 인덱스에 요소 삽입
링크드 리스트가 배열에 비해 뚜렷한 장점을 갖는 연산이다.
배열에서 0번째 인덱스에 요소를 삽입하기 위해 뒤에 따라오는 나머지 데이터를 한 셀씩 오른쪽으로 옮겨야 하는 반면,
링크드 리스트는 리스트 앞쪽에 요소를 삽입하는 데 딱 한 단계,O(1)만 걸린다.
2. 마지막 인덱스에 요소 삽입
그러나 반대로 마지막 인덱스에 요소를 삽입한다고 하면, 배열이 O(1)으로 요소를 추가할 수 있는 반면,
링크드 리스트는 마지막 노드를 검색하는 O(N)단계 + 삽입하는 O(1)단계가 필요하게 되어 배열이 훨씬 높은 효율성을 갖게 된다.
3. 중간에 요소 삽입
배열과 링크드 리스트 모두 평균적인 효율성을 갖게 된다.
삭제
1. 0번째 인덱스에서 요소 삭제
링크드 리스트에서는 O(1)단계면 된다. 단순히 첫 번째 노드가 두 번째 노드를 가리키게 하면 되기 때문이다.
반면 배열은 첫 번째 요소를 삭제하면 나머지 데이터를 모두 한 셀씩 왼쪽으로 시프트해야 하므로 효율성이 O(N)이 된다.
2. 마지막 인덱스에서 요소 삭제
링크드 리스트에서 마지막 노드를 삭제하는 경우는 O(N) + O(1)단계이다.
리스트 가장 앞에서부터 링크를 따라가 끝에서 두 번째 노드를 검색하는 절차와 그 노드가 null을 가리키는 링크를 넣어주는 단계가 필요하기 때문이다.
반면 배열은 바로 마지막 요소를 삭제하면 되니 O(1)의 효율성을 갖는다.
3. 중간에서 요소 삭제
여기서도 배열과 링크드 리스트 모두 평균적인 효율성을 갖는다.
요약
| 연산 | 배열 | 링크드 리스트 |
|---|---|---|
| 읽기 | O(1) | O(N) |
| 검색 | O(N) | O(N) |
| 삽입 | O(N) (끝에서부터 하면 O(1)) | O(N) (앞에서부터 하면 O(1)) |
| 삭제 | O(N) (끝에서부터 하면 O(1)) | O(N) (앞에서부터 하면 O(1)) |
많은 요소를 한번에 삭제할 때
사실 링크드 리스트가 진가를 발휘하는 경우는 한 리스트를 검사해서 많은 요소를 한번에 삭제할 때다.
왜냐하면 링크드 리스트에서는 리스트 전체를 살펴보면서 삭제가 필요하면 그저 그 노드의 링크가 적절한 노드를 가리키도록 바꾸는 한 단계만 있으면 되기 때문에, 각 삭제마다 딱 한 단계가 걸린다. (배열처럼 나머지 요소들을 앞당기거나 미룰 필요가 없기 때문이다.)
링크드리스트의 종류
1) 단일 연결 리스트 (Singly Linked List)

2) 이중 연결 리스트 (Doubly Linked List)

3) 환형 리스트 (Circular Linked List)

Reference 📕
*본 포스팅은 아래 도서/사이트들을 참고 및 인용하여 작성되었습니다.
학습단계로 잘못된 정보가 있을 수 있습니다. 잘못된 부분에 대해 알려주시면 곧바로 정정하도록 하겠습니다 😊
제이 웬그로우, 『누구나 자료구조와 알고리즘』, 길벗(2018)

https://noahlogs.tistory.com/27
https://velog.io/@dion/big-o-notation
링크드리스트 이미지 출처: https://www.programiz.com/dsa/linked-list-types