📌가설 검정 중 교차분석(카이제곱, 카이스퀘어, chi2)
카이제곱분포를 사용 - 데이터의 분산이 퍼져 있는 모습을 분포로 만든 것
범주형 자료를 사용
📖일원카이제곱
변인 : 단수 - 적합도(선호도) 검정) 교차분할표 사용 X
카이 제곱 검정은 goodness of fit(적합성) 검정이라고도 부른다.
SciPy stats 서브패키지의 chisquare 명령을 사용한다.
📖이원카이제곱
변인 : 복수 - 독립성, 동질성 검정 : 교차분할표 사용 O
두 개 이상의 집단 또는 범주의 변인을 대상으로 동질성 or 독립성 검정.
유의확률에 의해서 집단 간에 '차이가 있는가? 없는가?' 로 가설을 검정한다.
📖카이제곱 구하는 공식
모집단의 모수를 추정하기 위해 샘플 데이터로 검정통계량 X² 값을 구해 이를 사용
X² = Σ(관측값 - 기댓값)² / 기댓값
한번 샘플 자료를 가져와서 가설을 세워보자
📝가설 설정
가설설정은 대립을 먼저 세우고 귀무를 정한다.
- 귀무 가설 : 벼락치기 공부하는 것과 합격 여부는 관계가 없다.
- 대립 가설 : 벼락치기 공부하는 것과 합격 여부는 관계가 있다.
import pandas as pd
data = pd.read_csv('../testdata/pass_cross.csv', encoding='euc-kr')
print(data.head(3))
>>
공부함 공부안함 합격 불합격
0 1 0 1 0
1 1 0 1 0
2 0 1 0 1위의 출력 결과를 통해 정의
- 공부함 : 1, 공부안함 : 0, 합격 : 1, 불합격 : 0
이런식으로 미리 정의를 해놓고 다시 시작해보았다.
# 벼락치기 공부해서 합격한 인원
print(data[(data['공부함'] == 1) & (data['합격'] == 1)].shape[0])
>> 18
# 벼락치기 공부했는데 불합격한 인원
print(data[(data['공부함'] == 1) & (data['불합격'] == 1)].shape[0])
>> 7
ctab = pd.crosstab(index=data['공부안함'], columns=data['불합격'], margins=True)
ctab.columns=['합격', '불합격', '행합']
ctab.index=['공부함', '공부안함', '열합']
print(ctab) # 관측 값 구함
>>
합격 불합격 행합
공부함 18 7 25
공부안함 12 13 25
열합 30 20 50
# 기대값(도수) = (각 행의 주변합) * (각열의 주변합) / 총합
>>
15 10
15 10
# 행합과 열합은 제외하였다.
# X² = Σ(관측값 - 기댓값)² / 기댓값
chi_value = (18 - 15)**2 / 15 + (7-10)**2 / 10 + \
(12 - 15)**2 / 15 + (13 - 10)**2 / 10
print('카이제곱 :', chi_value)
>> 카이제곱 : 3.0카이제곱 검정 통계량 값(X²) = 3.0
📖평가 방법 1 (카이제곱표 사용 방법)
📝자유도
df(자유도) = N(사례수) - K(통계적 제한 조건 수)
2행 2열 이므로 나오는 값은
- (행개수 - 1) (열개수 - 1)
(2-1) (2-1) = 1
자유도는 1이 나왔다.
📖카이제곱표로 임계값 확인
카이 제곱표를 먼저 확인해보자
출처 : https://math100.tistory.com/45
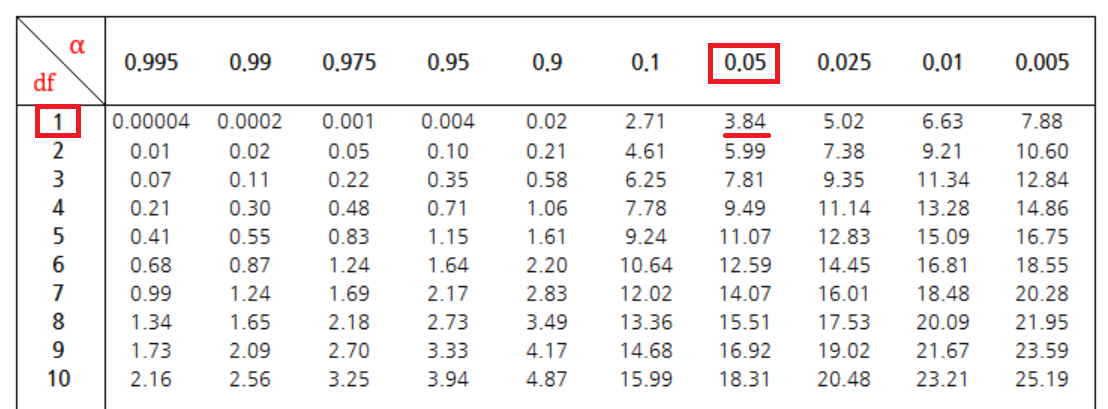
df 는 자유도, α(알파)는 유의수준이다.
자유도는 위에서 값 1이 나왔고, 유의수준은 0.05로 정의하였으니
- 임계값은 3.84 가 된다.
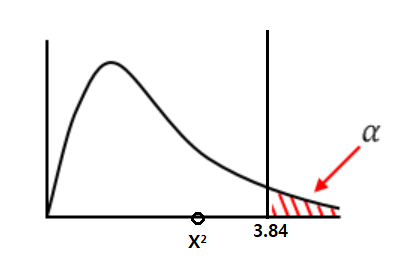
- 평가 : 카이제곱 검정 통계량 값(X²=3.0)이 임계값(3.84) 보다 작으므로 귀무 채택역 내에 있다.
∴(그러므로) 귀무 가설 채택 : 벼락치기 공부하는 것과 합격 여부는 관계가 없다.
위에 수집된 자료는 우연히 발생한 데이터라고 판단할 수 있다.
📖평가 방법 2 (p-value 사용)
import scipy.stats as stats
chi2, p, dof, expected = stats.chi2_contingency(ctab)
print('test statistic : {}, p-value : {}'.format(chi2, p))
>> test statistic : 3.0, p-value : 0.5578254003710748
# ps. 카이제곱 검정 통계량 값 과 p-value 는 반비례 관계이다.📝stats.chi2_contingency()
scipy.stats 라이브러리에서 제공해주며 이원카이제곱에서 카이제곱(chi2)과 p(p-value), dof(자유도), expected(기대치) 를 한번에 구해주는 메소드이다.
- 평가 : 유의확률(p-value : 0.5578254003710748) > 유의수준(알파, 0.05) 이므로 귀무 채택
📝이원 카이제곱 검정 예시
'''
# 이원카이제곱 : 교차분할표 사용
: 두 개 이상의 집단 또는 범주의 변인을 대상으로 동질성 or 독립성 검정.
: 유의확률에 의해서 집단 간에 '차이가 있는가? 없는가?' 로 가설을 검정한다.
# 교육 수준과 흡연률 간의 관련성을 분석
'''
import pandas as pd
import scipy.stats as stats
'''
- 귀무 : 교육 수준과 흡연률 간의 관련이 없다.(독립이다.)
- 대립 : 교육 수준과 흡연률 간의 관련이 있다.(독립이 아니다.)
'''
data = pd.read_csv('../testdata/smoke.csv')
print(data.head(3))
print(data['education'].unique()) # [1 2 3]
print(data['smoking'].unique()) # [1 2 3]
# 두개의 변인, 각각 범주형 데이터이다.
ctab = pd.crosstab(index=data['education'], columns=data['smoking'])
ctab.index = ['대학원졸', '대졸', '고졸']
ctab.columns = ['과흡연', '보통', '노담']
print(ctab)
>>
과흡연 보통 노담
대학원졸 51 92 68
대졸 22 21 9
고졸 43 28 21
>>
# 이원 카이제곱일 경우 stats.chi2_contingency() 을 사용한다.
chi2, p, dof, _ = stats.chi2_contingency(ctab)
print('chi2:{}, p:{}, dof:{}'.format(chi2, p, dof))
>> chi2:18.910915739853955, p:0.0008182572832162924, dof:4
'''
PS. 자유도가 1일 경우, 관측치는 0.5씩 기대값으로 옮기는
Yates correction(야트 보정) 이 적용되어 검정통계량이 더 낮게 나오게 됩니다.
결과적으로 p-value가 0.05 보다 낮으므로 귀무가설을 기각하여
두 변수가 독립이 아니라고 판단할 수 있다.(내부적으로 일어난다.)
- 결과 값
chi2:18.910915739853955, p:0.0008182572832162924, dof(자유도):4
해석 : p(=0.0008) < 0.05 이므로 귀무가설 기각
교육 수준과 흡연률 간의 관련이 있다 라는 결론을 얻을 수 있다.
후속조치...
'''