📖 선형회귀분석의 기존 가정 충족 조건
- 선형성 : 독립변수(feature)의 변화에 따라 종속변수도 일정 크기로 변화해야 한다.
- 정규성 : 잔차항(오차항)이 정규분포를 따라야 한다.
- 독립성 : 독립변수의 값이 서로 관련되지 않아야 한다.
- 등분산성 : 그룹간의 분산이 유사해야 한다. 독립변수의 모든 값에 대한 오차들의 분산은 일정해야 한다.
- 다중공선성 : 다중회귀 분석 시 두 개 이상의 독립변수 간에 강한 상관관계가 있어서는 안된다.
✍️입력
import statsmodels.formula.api as smf
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.rc('font', family='malgun gothic')
# 첫번째 컬럼을 제외하고 사용하기 위해 usecols 파라미터 사용
advdf = pd.read_csv('../testdata/Advertising.csv', usecols=[1,2,3,4])
print(advdf.head(3), ' ', advdf.shape)
'''
tv radio newspaper sales
0 230.1 37.8 69.2 22.1
1 44.5 39.3 45.1 10.4
2 17.2 45.9 69.3 9.3 (200, 4)
'''PS. 원래 같은 경우에 dataset 에서 70% 학습용, 30% 검정용으로 분리하여 계산한다.
📝train / test 분리하는 이유?
출처 https://teddylee777.github.io/scikit-learn/train-test-split/
먼저, train / test 를 분리하는 목적을 정확히 알아야합니다.
정확히 말하면, train / test 가 아닌 train / validation 으로 볼 수 있습니다. (어차피 용어의 차이긴 하지만요)
머신러닝 모델에 train 데이터를 100% 학습시킨 후 test 데이터에 모델을 적용했을 때 성능이 생각보다 않 나오는 경우가 많습니다 (거의 99.999% 는요)
이러한 현상을 보통 Overfitting 되었다라고 합니다.
즉, 모델이 내가 가진 학습 데이터에 너무 과적합되도록 학습한 나머지, 이를 조금이라도 벗어난 케이스에 대해서는 예측율이 현저히 떨어지기 때문이라고 이해하시면 됩니다.
그렇기 때문에 Overfitting을 방지하는 것은 전체적인 모델 성능을 따져보았을 때 매우 중요한 프로세스 중 하나입니다.
- train_test_split 함수를 사용하여 분리 가능합니다.
from sklearn.datasets import load_iris # 샘플 데이터 로딩
from sklearn.model_selection import train_test_split
# load sample
dataset = load_iris()
data = dataset['data']
target = dataset['target']
# train_test_split
x_train, x_valid, y_train, y_valid = train_test_split(data, target, test_size=0.2, shuffle=True, stratify=target, random_state=34)📝 train_test_split 옵션 값 설명
- 📌test_size
테스트 셋 구성의 비율을 나타냅니다. train_size의 옵션과 반대 관계에 있는 옵션 값이며, 주로 test_size를 지정해 줍니다. 0.2는 전체 데이터 셋의 20%를 test (validation) 셋으로 지정하겠다는 의미입니다. default 값은 0.25 입니다. - 📌shuffle
default=True 입니다. split을 해주기 이전에 섞을건지 여부입니다. 보통은 default 값으로 놔둡니다. - 📌stratify
default=None 입니다. classification을 다룰 때 매우 중요한 옵션값입니다. stratify 값을 target으로 지정해주면 각각의 class 비율(ratio)을 train / validation에 유지해 줍니다. (한 쪽에 쏠려서 분배되는 것을 방지합니다) 만약 이 옵션을 지정해 주지 않고 classification 문제를 다룬다면, 성능의 차이가 많이 날 수 있습니다. - 📌random_state
세트를 섞을 때 해당 int 값을 보고 섞으며, 하이퍼 파라미터를 튜닝시 이 값을 고정해두고 튜닝해야 매번 데이터셋이 변경되는 것을 방지할 수 있습니다.
print('단순선형회귀모델 : tv(독립변수), sales(종속변수) 지정')
print('상관계수(r) :', advdf.loc[:,['sales', 'tv']].corr())
'''
상관계수(r) :
sales tv
sales 1.000000 0.782224
tv 0.782224 1.000000
* 0.782224 : 강한 양의 상관관계가 확인된다. 인과관계가 있다고 가정하고 회귀모델 작성
'''
# lm = smf.ols(formula='sales ~ tv', data=advdf)
# lm = lm.fit()
lm = smf.ols(formula='sales ~ tv', data=advdf).fit()
# print(lm.summary())
print(lm.rsquared)
>> 0.611875050850071
# 시각화
plt.scatter(advdf.tv, advdf.sales) # 실제값
y_pred = lm.predict(advdf.tv) # 예측값
plt.plot(advdf.tv, y_pred, c='blue')
plt.xlabel('tv 매체로 광고비')
plt.ylabel('판매 실적')
plt.title('선형회귀')
plt.xlim(-50, 400)
plt.ylim(ymin=0)
plt.show()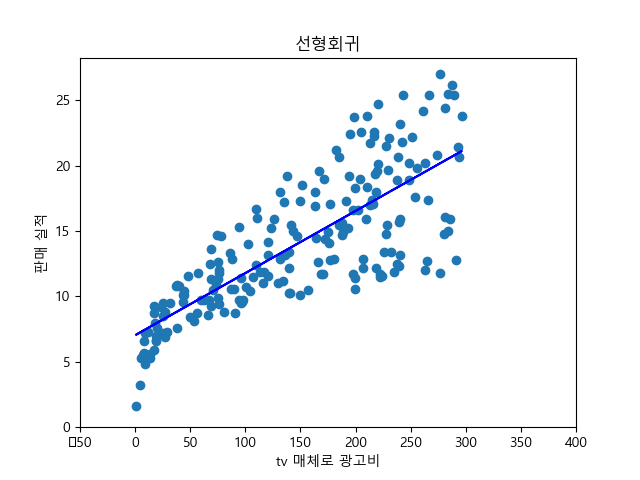
# 모델 검정
pred = lm.predict(advdf.tv[:5]) # 사실은 검정용 데이터를 따로 준비한 후 사용하는것이 원칙
print('예측값 :\n', pred.values)
# [17.97077451 9.14797405 7.85022376 14.23439457 15.62721814]
print('실제값 :\n', advdf.sales[:5].values)
# [22.1 10.4 9.3 18.5 12.9]
# 예측 : 새로운 tv 값으로 sales 를 추정
x_new = pd.DataFrame({'tv':[110.5, 220.6, 500.8]})
pred_new = lm.predict(x_new)
print('추정값 :\n', pred_new)
'''
추정값 :
0 12.285392
1 17.519176
2 30.838943
dtype: float64
'''이번엔 독립변수가 2개 인 다중선형회귀모델 보자
📖다중선형회귀모델
print(advdf.corr())
'''
tv radio newspaper sales
tv 1.000000 0.054809 0.056648 0.782224
radio 0.054809 1.000000 0.354104 0.576223
newspaper 0.056648 0.354104 1.000000 0.228299
sales 0.782224 0.576223 0.228299 1.000000
'''
# lm_mul = smf.ols(formula = 'sales ~ tv + radio + newspaper', data=advdf).fit()
# print(lm_mul.summary())
# newspaper 가 pvalue > 0.05 이므로 newspaper는 독립변수에서 제외한다.
lm_mul = smf.ols(formula = 'sales ~ tv + radio', data=advdf).fit()
print(lm_mul.summary())
# 예측 : 새로운 tv, radio 값으로 sales 를 추정
x_new2 = pd.DataFrame({'tv':[110.5, 220.6, 500.8], 'radio':[10.1, 30.2, 100.1]})
pred_new2 = lm_mul.predict(x_new2)
print('추정값 :\n', pred_new2.values)
'''
추정값 :
[ 9.87574867 18.69203777 44.6533334 ]
'''📖선형회귀분석의 기존 가정 충족 조건 검사하기
'''
*** 선형회귀분석의 기존 가정 충족 조건 ***
- 선형성 : 독립변수(feature)의 변화에 따라 종속변수도 일정 크기로 변화해야 한다.
- 정규성 : 잔차항(오차항)이 정규분포를 따라야 한다.
- 독립성 : 독립변수의 값이 서로 관련되지 않아야 한다.
- 등분산성 : 그룹간의 분산이 유사해야 한다. 독립변수의 모든 값에 대한 오차들의 분산은 일정해야 한다.
- 다중공선성 : 다중회귀 분석 시 두 개 이상의 독립변수 간에 강한 상관관계가 있어서는 안된다.
'''
# 예측값
fitted = lm_mul.predict(advdf.iloc[:,0:2])
# 잔차항 구하기 : 실제 값 - 예측값
residual = advdf.sales - fitted
print('실제 값 :', advdf.sales[:5].values)
print('예측 값 :', fitted[:5].values)
print('잔차 값 :', residual[:5].values)
print('잔차값의 평균 :', np.mean(residual))
'''
실제 값 : [22.1 10.4 9.3 18.5 12.9]
예측 값 : [20.55546463 12.34536229 12.33701773 17.61711596 13.22390813]
잔차 값 : [ 1.54453537 -1.94536229 -3.03701773 0.88288404 -0.32390813]
잔차값의 평균 : 5.5333515547317806e-15
'''📌선형성
선형성은 직선처럼 똑바른 도형, 또는 그와 비슷한 성질을 갖는 대상이라는 뜻으로, 이러한 성질을 갖고 있는 변환 등에 대하여 쓰는 용어
import seaborn as sns
print('\n-------- 선형성(예측값과 잔차가 비슷한 패턴 유지) --------')
'''
선형성 확인 시각화 regplot()
python seaborn의 regplot은
scatter plot과 line plot을 함께 볼 수 있는 데이터 시각화 방법입니다.
'''
sns.regplot(x=fitted, y=residual, lowess=True, line_kws={'color':'red'})
plt.plot([fitted.min(), fitted.max()], [0,0], '--', color='grey')
plt.show() 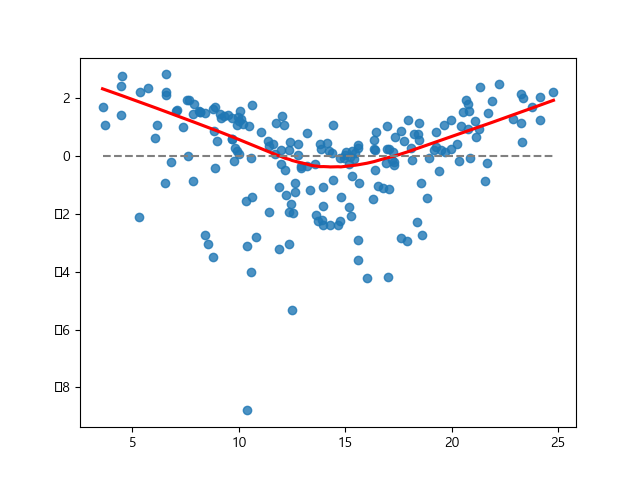
잔차의 추세선이 파선을 기준으로 일정하지 않음. 하여 선형성 만족하지 못한다.
📌정규성
print('\n-------- 정규성(잔차가 정규성 유지) --------')
import scipy.stats
sr = scipy.stats.zscore(residual)
'''
scipy.stats.zscore()
z 점수를 계산합니다.
표본 평균 및 표준 편차를 기준으로 표본에 있는 각 값의 z 점수를 계산합니다.
'''
(x, y), _ = scipy.stats.probplot(sr)
'''
scipy.stats.probplot()
확률도의 분위수를 계산하고 선택적으로 플롯을 표시합니다.
지정된 이론적 분포(기본적으로 정규 분포)의 분위수에 대한 표본 데이터의 확률도를 생성합니다.
probplot선택적으로 데이터에 가장 적합한 라인을 계산하고
Matplotlib 또는 주어진 플롯 함수를 사용하여 결과를 플로팅합니다.
'''
sns.scatterplot(x=x, y=y)
plt.plot([-3, 3], [-3, 3], '--', color='grey')
plt.show()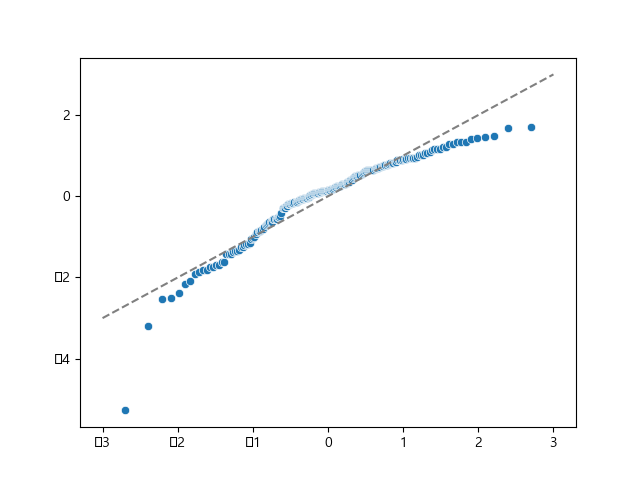
정규성은 불만족, 커브를 그리는 것이 다소 의심스럽다.
📌독립성
독립성(잔차가 독립성 유지, 자기상관이 있는지 확인(독립적이려면 자기상관이 없어야 한다.)
- 자기상관 : 어떤 확률변수가 주어졌을 때, 서로 다른 두 시점에서의 관측치 사이에 나타나는 상관성을 “자기상관성(autocorrelation)”이라 한다.
- OLS Regression Results 에서 Durbin-Watson : 2.081 인것을 확인 할수 있다
OLS Regression Results ============================================================================== Dep. Variable: sales R-squared: 0.897 Model: OLS Adj. R-squared: 0.896 Method: Least Squares F-statistic: 859.6 Date: Thu, 11 May 2023 Prob (F-statistic): 4.83e-98 Time: 14:04:12 Log-Likelihood: -386.20 No. Observations: 200 AIC: 778.4 Df Residuals: 197 BIC: 788.3 Df Model: 2 Covariance Type: nonrobust ============================================================================== coef std err t P>|t| [0.025 0.975] ------------------------------------------------------------------------------ Intercept 2.9211 0.294 9.919 0.000 2.340 3.502 tv 0.0458 0.001 32.909 0.000 0.043 0.048 radio 0.1880 0.008 23.382 0.000 0.172 0.204 ============================================================================== Omnibus: 60.022 Durbin-Watson: 2.081 Prob(Omnibus): 0.000 Jarque-Bera (JB): 148.679 Skew: -1.323 Prob(JB): 5.19e-33 Kurtosis: 6.292 Cond. No. 425. ==============================================================================Durbin-Watson 테스트는 회귀 모델에서 잔차의 자기 상관관계에 대한 척도입니다.
Durbin-Watson 테스트는 0~4의 척도를 사용하며, 0~2 값은 양의 자기 상관관계를 나타내며 2~4 값은 음의 자기 상관관계를 나타냅니다.
즉, Durbin-Watson 값이 2에 가까울수록 독립성이 강해진다.
- 결론 : Durbin-Watson값이 2.081 이므로 독립성 만족한다.
📌등분산성
print('\n-------- 등분산성(잔차의 분산이 일정한지 확인) --------')
# 비모수적 최소모델을 추정해라 (lowess=True)
sns.regplot(x=fitted, y=np.sqrt(np.abs(sr)), lowess=True, line_kws={'color':'red'})
plt.show() 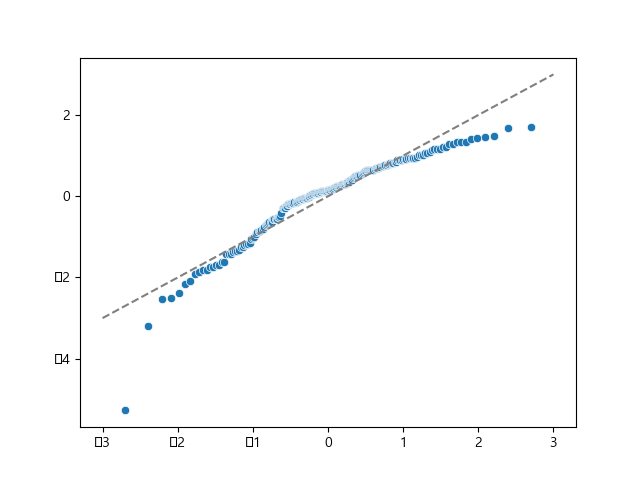
- 평균을 기준으로 데이터 골고루 퍼지지 않음, 등분산성 불만족
붉은 선이 평탄한 선을 그려야 등분산성을 만족하나, 현재 그래프에서는 커브를 그리고 있어 불만족이다.
📌다중공선성
다중공선성(multicollinearity) : 하나의 독립변수가 다른 여러 개의 독립변수들로 잘 예측되는 경우
- (다중)공선성이 있으면:
계수 추정이 잘 되지 않거나 불안정해져서 데이터가 약간만 바뀌어도 추정치가 크게 달라질 수 있다
계수가 통계적으로 유의미하지 않은 것처럼 나올 수 있다
print('\n-------- 다중공선성(독립변수들 간의 강한 상관관계 확인) --------')
'''
VIF란, Variance Inflation Factor의 약자로서, 분산 팽창 인수라고 합니다.
이 값은 다중회귀분석에서 독립변수가 다중 공선성(Multicollnearity)의 문제를 갖고 있는지
판단하는 기준이며, 주로 10보다 크면 그 독립변수는 다중공선성이 있다고 말합니다.
'''
from statsmodels.stats.outliers_influence import variance_inflation_factor
print(variance_inflation_factor(advdf.values, 1)) # tv
'''
12.570312383503682
값이 10보다 크므로 다중공선성이 있다고 판단
'''
print(variance_inflation_factor(advdf.values, 2)) # radio
'''
3.1534983754953845
값이 10보다 작으므로 다중공선성이 없다고 판단
'''📝참고 ) Cook's distance : 아웃라이어 확인 지표
# 참고 ) Cook's distance : 아웃라이어 확인 지표
from statsmodels.stats.outliers_influence import OLSInfluence
cd, _ = OLSInfluence(lm_mul).cooks_distance # 아웃라이어 값 반환
print(cd.sort_values(ascending=False).head())
'''
130 0.258065
5 0.123721
35 0.063065
178 0.061401
126 0.048958
dtype: float64
'''
import statsmodels.api as sm
sm.graphics.influence_plot(lm_mul, criterion='cooks')
plt.show()
# 그래프에 보이는 원이 클수록 아웃라이어일 확률이 크다.
print(advdf.iloc[[130, 5, 35, 178, 126]]) # 아웃라이어 의심 인덱스
'''
tv radio newspaper sales
130 0.7 39.6 8.7 1.6
5 8.7 48.9 75.0 7.2
35 290.7 4.1 8.5 12.8
178 276.7 2.3 23.7 11.8
126 7.8 38.9 50.6 6.6
'''