[프로그래머스] 제곱수 판별

나의 풀이의 문제점

function solution(n) {
    for(let i=1; i < n; i++) {
        if(n % i === 0) {
            return 1;
        } return 2;
    }
}

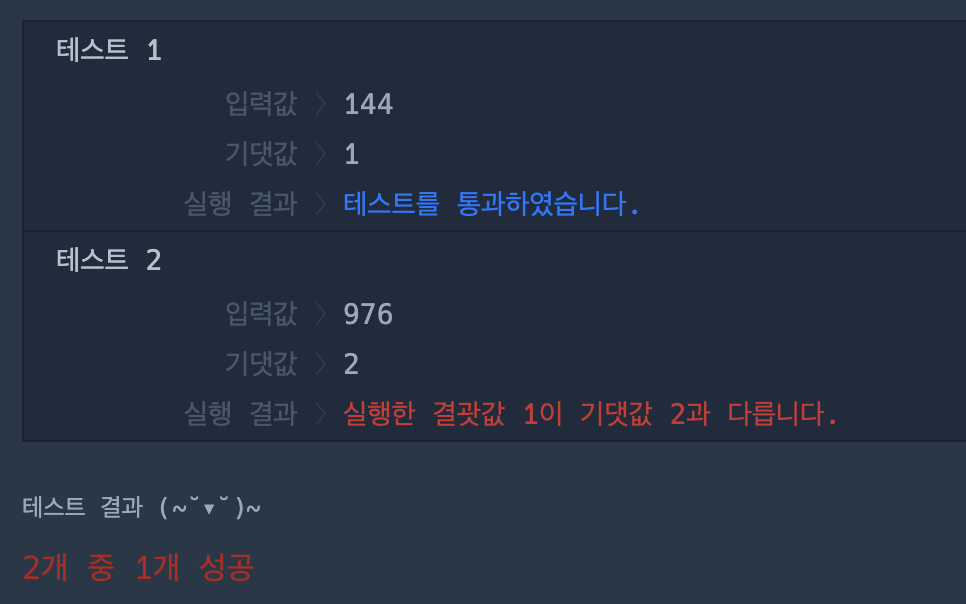
먼저 제곱수의 특징에 대해서 알아봤다.
제곱수의 특징은 약수가 홀수개 라는 것이다.
제곱수가 되면 나머지가 0이 될거라는 생각이 들어 n % i를 해보니 홀수도 나머지가 0이 될 수 있다는 것을 인지하였다.
찾아보다가 제곱근을 이용하여 제곱수를 계산하는 방법도 있다고 해서 다른사람들의 풀이를 찾아봤다.

---

다른사람 풀이(1)

function solution(n) {
  return Number.isInteger(Math.sqrt(n)) ? 1 : 2;
}

Math.sqrt()는 제곱근을 반환한다.

 Math.sqrt(9); // 3
 Math.sqrt(2); // 1.414213562373095
 Math.sqrt(1); // 1
 Math.sqrt(0); // 0
 Math.sqrt(-1); // NaN

isInteger로 정수값을 판별하는 이유는 위와같이 Math.sqrt()가 실수도 반환하기 때문이다.

다른사람 풀이(2)

function solution(n) {
    for (let i=0; i*i <= n; i++) {
        if (i*i === n) return 1
    }
    return 2;
}

제곱근이기 때문에 조건문에 i i === n를 사용해봤었는데 이것 또한 여러 경우의 수에 맞는 알고리즘이 아니었다.
for문의 조건을 i i <= n으로 하게되면 i의 범위가 현저히 작아지고 그 안에서 최소공배수를 찾아나갈 수 있다.