백준 자바 15649 N과 M(1)

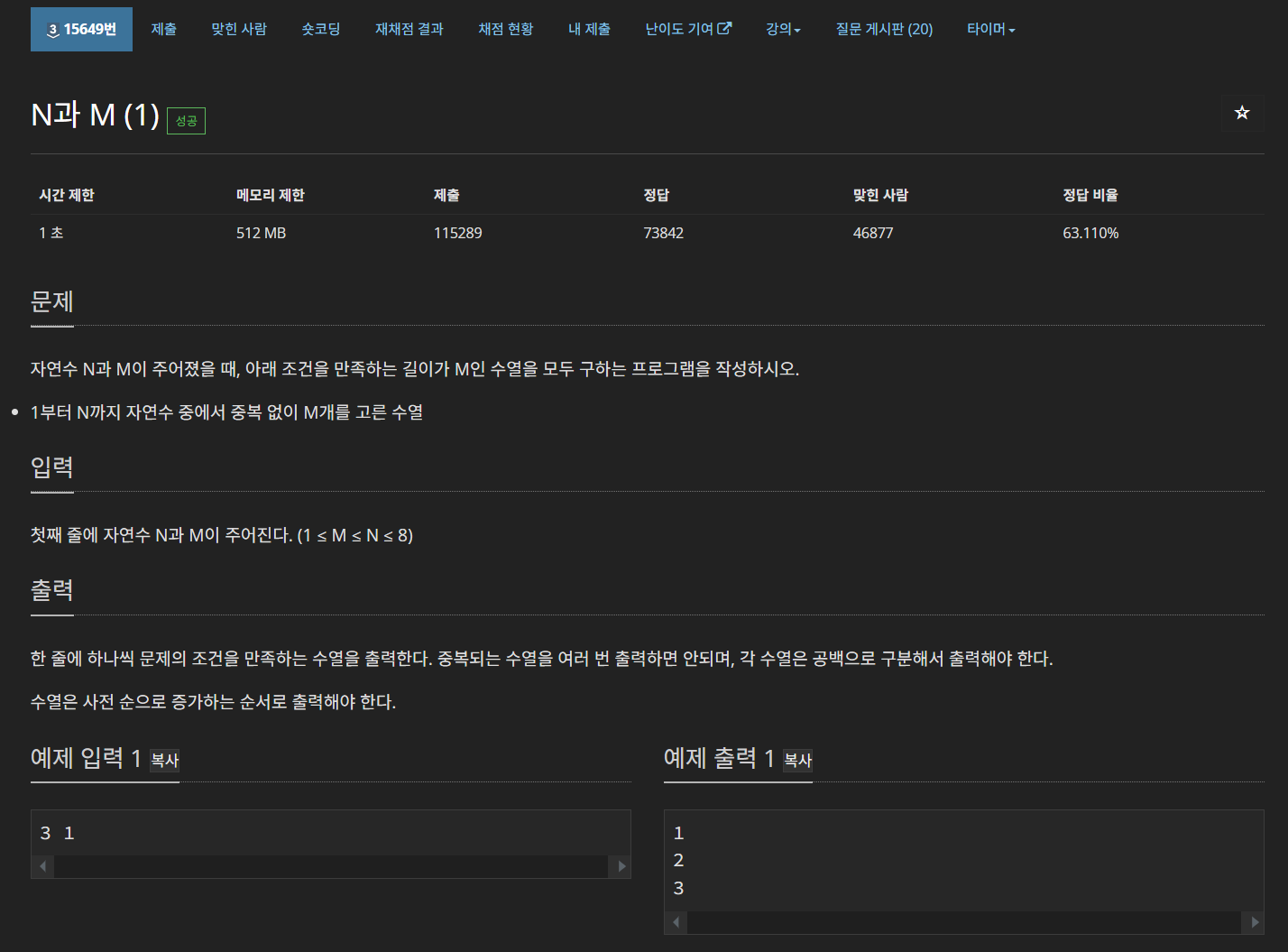
이 문제는 원래 풀어야 되는 문제는 아니였지만, 15650 N과 M(2)가 있기에
연습겸 풀었다.

package test11;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;

public class Ox11_Q4_1 {
	static StringBuilder sb;
	static int n,m;
	static int cnt;
	static boolean [] issued ;
	static int [ ] put;
	
	// 백준 15649 S3 ( N과 M(1) )
	public static void main(String args []) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		sb = new StringBuilder();
		
		n = Integer.parseInt(st.nextToken());
		m = Integer.parseInt(st.nextToken());
		issued = new boolean[n+1];
		put = new int[m+1];
		br.close();
		
		checkN(0);
		System.out.println(sb.toString());	

	}

	public static void checkN(int cur) {
		if (cur == m) {
			for (int i = 0; i < m; i++) {
				sb.append(put[i] + " ");
			}
			sb.append("\n");
			return;
		} // if fin

		for (int i = 1; i <= n; i++) {
			if (!issued[i]) {
				put[cur] = i;
				issued[i] = true;
				checkN(cur + 1);
				issued[i] = false;
			}// if fin
		} // for fin
	}// checkN fin

}

N-Queen 문제와 같이 강의에 있었기에 참고하면서 문제를 해결하였다.
함수 checkN 는 m개의 변수를 받아 수열화 할 것이고, cur번째 값들을 수열을 저장하는 배열에
순차적으로 더한다. 그 과정에서 m과 같아지면 완성된 수열을 sb에 차근차근 누적하는 구문이다.
이 과정에서 N-Queen과 같이 재귀하는 구문이 실행되고나면 차근차근 초기화 시켜주는게 포인트이다.

풀면서 느낀점이 백트래킹은 재귀 +Dfs 느낌인데, 내가 제대로 이해한게 맞는지 모르겠다.

굿