백준 자바 1699 제곱수의 합

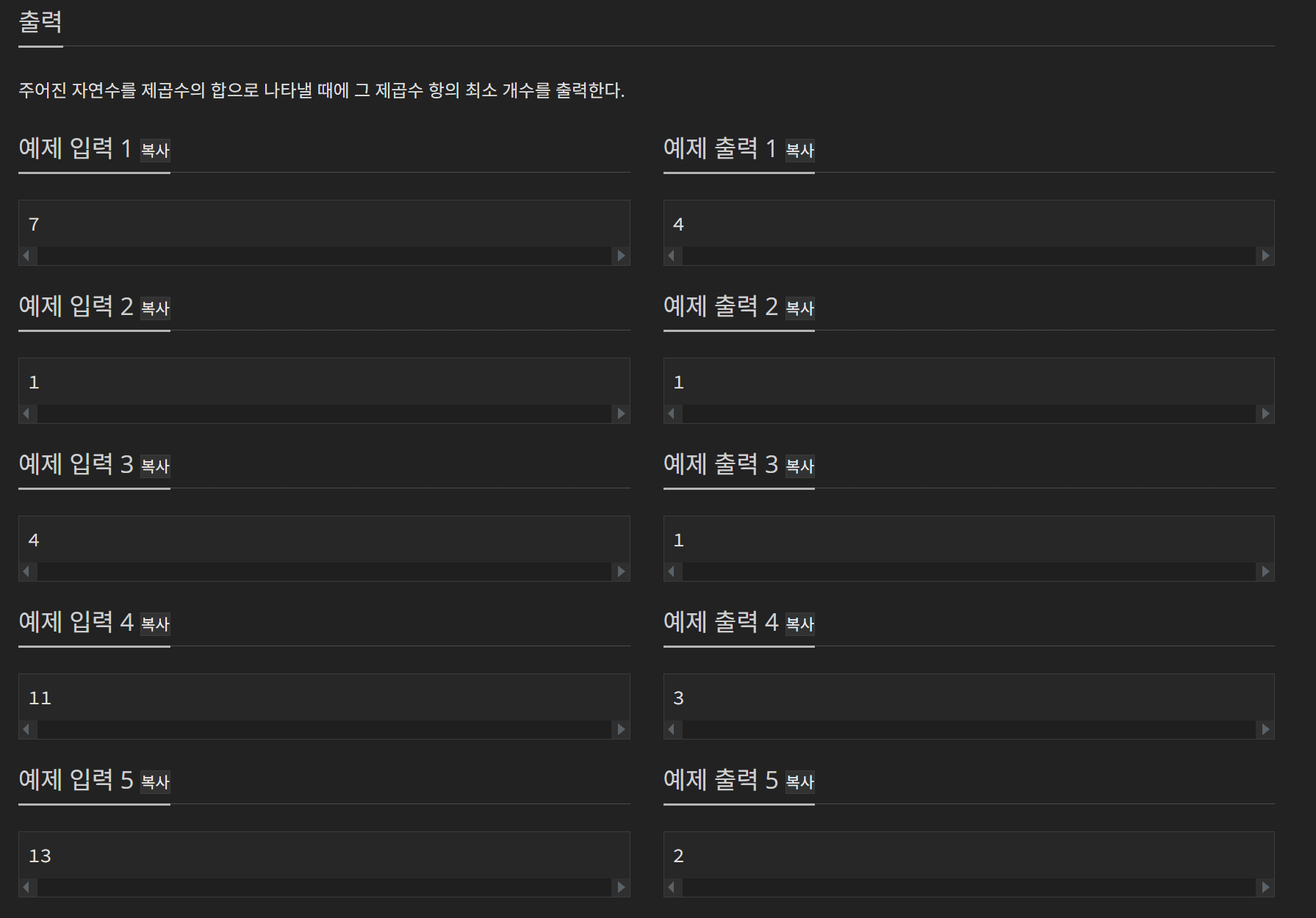
이 문제는 어떤 자연수 N이 주어지고, 해당 수를 제곱수들의 합으로 나타내는 것이다.
예를들면, N = 30이라했을때, 30 = 25(5 ^2) + 4(2^2) + 1 (1^2) 이므로, 개수는 3이다.

따라서, N이 주어졌을 때, n보다 작은 가장 큰 제곱 수를 구하고 이를 뺀 후, 남은 수 n 에서 가장 큰 제곱 수를 계속 반복해서 빼는 방식으로 구현하였다.

package test13;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;
import java.util.PriorityQueue;
import java.util.StringTokenizer;

public class Ox13_Q4_1 {
	static int count =0;
	// 백준 1699 S2 
	public static void main(String [] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int n = Integer.parseInt(br.readLine());
		
		maxRoot(n);
		
		System.out.println(count);
	
	}
	
	public static int maxRoot(int n) {
		if(n == 0) {
			return count;
		}
		int maxN = 0;
		for(int i = 1; i*i<=n; i++) {
			 if(i*i<=n) {
				 maxN = i;
			 }
		}// for fin
		count++;
		maxRoot(n- maxN*maxN);
		return count;
	}

}

하지만, 오류가 발생했다.
반례를 찾아보니 n = 18 인경우
내가 푼 방식으로 해결하면
18 = 16 + 1 + 1 로 3 이 나오는데, 실제 답은
9 + 9 로 2여야한다.

따라서, 점화식을 활용해서 이 문제를 풀어야겠다고 생각했다.
예를들어 dp[i]의 값은 그냥 순수하게 i번째 값과,
중간에 제곱근이 있는경우 그 값을 뺀 dp번째 값의 +1을 계속 비교해줘야한다.

이게 무슨 소리냐면, 예를들어 i = 16인경우,
( dp[16], dp[16-4] +1 )
( dp[16], dp[16-9] +1 )
( dp[16], dp[16-16] +1)

이런식으로 비교하면 답을 구할 수 있다.

package test13;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;
import java.util.PriorityQueue;
import java.util.StringTokenizer;

public class Ox13_Q4_2 {
	// 백준 1699 S2 
	public static void main(String [] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int n = Integer.parseInt(br.readLine());
		int count = maxRoot(n);
		
		System.out.println(count);
	
	}
	
	// 계산하기
	public static int maxRoot(int n) {
		int dp [] = new int [n+1]; // 0부터 n까지 사용하기 위함
		Arrays.fill(dp, Integer.MAX_VALUE); // 초기에 제일 큰 값 세팅해서 최소 값 비교에 용이하게함
		dp[0] = 0;
		
		for(int i = 1; i<=n; i++) {
			 for(int j = 1; j*j<=i; j++ ) {
				 dp[i] = Math.min(dp[i], dp[i - j*j] +1 );
			 }
		}// for fin
		
		return dp[n];
	}// maxRoot fin
	

}

굿