The Byzantine Generals Problem - Leslie Lamport 리뷰(1)

이 포스트는 The Byzantine Generals Problem - Leslie Lamport을 읽고 저만의 방식으로 정리한 글입니다.

상황

전체적인 상황

비잔틴 장군 문제의 상황은 다음과 같다.

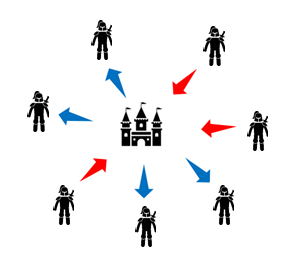
적 도시를 침공하기 위하여 비잔틴 군대의 각 부대들은 적 도시 주변에 주둔하고 있다. 각 부대는 장군들이 이끌며장군들끼리는 서로가 메신저를 통해서만 의사소통할 수 있다. 장군들은 해당 도시를 공격할지 안할지 정해야 하는데, 이 장군들 중에서는 배신한(traitor) 장군이 있어서 배신한 장군들은 각 부대들이 합의를 이뤄서 성공적인 공격을 하는 것을 방해한다.

이와 같은 상황에서 성공적인 침공을 위해서는 다음과 같은 조건을 만족하는 알고리즘이 필요하다.

1. 모든 충실한(loyal) 장군들은 같은 행동을 결정한다.
2. 배신한 장군들은 충실한 장군들이 나쁜 계획에 합의하도록 만들 수 없다.

조금 더 자세히

v(i)를 장군들끼리 의사소통을 위해 i번째 장군이 보낸 정보라고 할 때,

각 장군들은 v(1),v(2)...,v(n)을 취합해서 특정 행동을 결정하게 된다.(n:장군의 수)

v(i)를 이용해서 위 조건을 다시 표현한다면, 모든 i에 대하여

1. 어느(any) 두 충실한 장군은 같은 값의 v(i)를 받아야 한다.
2. i번째 장군이 충실하다면, 그가 보낸 정보 v(i)는 모든 충실한 장군들에 의해 사용되어야 한다.
   다시 말하여서, 어느 배신한 장군도 충실한 장군이 보낸 정보를 조작하거나 수정할 수 없다.

위 두 조건은 모두 i번째 장군이 보낸 정보에 관한 조건이다. 그렇다면, 우리는 모든 장군이 아닌, 한명의 장군이 자신의 정보(값)을 나머지에게 어떻게 전달하는지에 대하여서만 고려하여도 문제는 동일하다.

진짜 비잔틴 장군 문제의 형식

n명의 장군은 1명의 사령관(commander)과 n-1명의 장교(lieutenant)로 나눠지게 된다. 사령관은 장교들에게 지시를 내리는데 다음과 같은 조건을 만족해야 한다.

IC1. 모든 충실한 장교들은 같은 지시를 따라야 한다.
IC2. 만약 사령관이 충실하다면, 모든 충실한 장교는 그가 내린 지시를 따라야한다.

사령관이 충실한 경우에는 IC2를 만족하면 IC1이 자연스럽게 따라서 만족된다.

사령관이 충실한 경우, IC2 -> IC1

---

불가능한 경우

미리 얘기하자면, 장군들끼리 말을 통해서 의사소통을 하는 경우에는 전체의 2/3보다 충실한 장군이 많아야만 비잔틴 장군 문제의 해답이 존재한다.

장군 3명, 배신자 1명

문제를 간단히 하기 위하여, 우리는 장군이 내릴 수 있는 결정이 [공격,후퇴] 밖에 없다고 가정하자.

첫번째, 장교 2가 배신했을때

장교 1 입장에서 생각해보자. 충실한 사령관은 현재 공격하라는 지시를 장교들에게 내렸다. 그렇다면 IC2에 의하여 장교 1은 공격을 하여야 한다.

두번째, 사령관이 배신했을 때

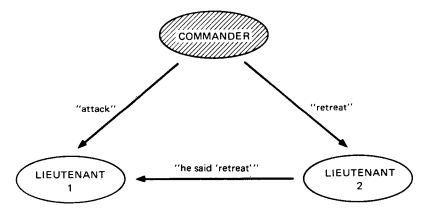
장교 1은 현재 누가 배신하였는지 알지 못하는 상태이다. 재밌는 사실은 장교 1이 받은 정보의 종류와 형태가 첫번쨰 경우와 분별이 불가능하다. 고로 장교 1은 장교 2의 말과는 관계없이 공격을 할 것이다.

장교 2도 마찬가지이다. 장교 2 역시 장교 1이 배신한 경우와 사령관이 배신한 경우를 받은 정보만으로는 분별이 불가능하기 때문에 결국 후퇴를 할 수 밖에 없고, 이 경우에 IC2를 위반하게 된다.

결론적으로 3명의 장교, 1명의 배신자 케이스에는 해답이 존재하지 않는다.

최대 장군 3m명, 배신자 m명

앞서 설명된 경우를 더 일반적으로 만든 케이스이다. 증명은 귀류법을 사용한다.

• 가정: 최대 장군 3m명에 배신자 m명인 경우에 비잔틴 장군 문제의 해답은 존재한다.

이제 모순을 보여서 가정이 틀렸다는 것을 증명하자.

혼선을 방지하기 위하여 우리는 알바니안 장군이 최대 3m명이고, 배신한 알바니안 장군이 m명인 비잔틴 장군 문제를 풀고 있다고 생각해보자. 그렇다면 우리는, 최대 알바니안 장군 m명을 1명의 비잔틴 장군으로 치환하여서 생각할 수 있다. 즉,

• 알바니안 사령관 1명 + 최대 알바니안 장교 (m-1)명 = 비잔틴 사령관 1명
• 최대 알바니안 장교 m명 = 비잔틴 장교 1명
• 최대 알바니안 장교 m명 = 비잔틴 장교 1명

이다. 만약 우리가, 알바니안 장군들에 대하여 IC1 & IC2를 만족하는 해답을 가지고 있다면, 그 해답은 이를 치환해서 만든 비잔틴 장군 3명, 배신자 1명의 케이스도 해결하여야 하지만, 앞서 알아봤듯이 이는 불가능하다.

결론적으로, 가정은 모순이고, 최대 장군 3m명에 배신자 m명인 경우에 비잔틴 장군 문제의 해답은 존재하지 않는다.

---

Oral Message 경우의 솔루션

전제 조건

가정

1. 모든 보내진 메시지는 올바르게 전달된다.

2. 받는 사람은 누가 메시지를 보내었는지 알 수 있다.

3. 메시지의 부재는 인지 가능하다.

이 외

• majority 함수
  만약 v(i) 값의 과반수가 v라면, majority(v(1),v(2),...,v(n)) = v
• 메시지가 부재하였을 때를 대비하여서 default 값은 후퇴이다.

Oral Message Algorithm OM(m)

우리는 OM(m)이 장군이 최소 3m+1명에 배신자 m명인 경우의 비잔틴 장군 문제를 해결할 수 있음을 보일 것이다.

OM(m)의 정의

우리는 귀납적으로 OM(m)을 정의한다. n은 총 장군의 수이다.

OM(0)

1. 사령관은 자신의 값을 모든 장교에게 전달한다.

2. 각 장교는 사령관으로부터 받은 값을 사용하고, 값을 받지 못하였다면 '후퇴'를 값으로 사용한다.

OM(m), m>0

1. 사령관은 자신의 값을 모든 장교에게 전달한다.

2. 모든 i에 대하여, v(i)를 i번째 장교가 사령관으로 부터 받은 값이라 하고, 만약 값을 받지 못하였다면 '후퇴'를 값으로 사용한다. 이후 i번째 장교는 OM(m-1)에서 사령관 역할을 하여서 나머지 n-2명의 장교들에게 v(i)를 전달한다.

3. 모든 i와 i가 아닌 각각의 j에 대하여 v(j)를 2.에서 OM(m-1)을 이용하여 i번째 장교가 j번째 장교로부터 받은 값이라 하고, 만약 값을 받지 못하였다면 '후퇴'를 값으로 사용한다. i번째 장교는 majority(v(1),v(2),...,v(n))을 값으로 사용한다.

예로 알아보는 OM 알고리즘

m = 1, n = 4의 OM(1) 을 2번 장교 기준으로 생각해보자. 배신자는 3번 장교이다.

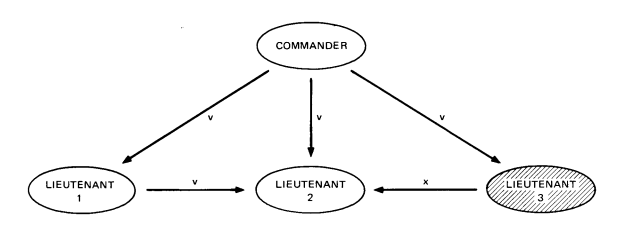
OM(1)

1. 사령관은 v라는 값을 모든 장교에게 전달한다.

2. OM 알고리즘을 따르는 충실한 1번 장교는 OM(0)에서 사령관 역할을 하여서 2번 장교에게 사령관으로부터 전달받은 값, v를 전달한다.
   하지만, 배신자 3번 장교는 OM 알고리즘을 따르지 않기에 2번 장교에게 다른 값 x를 전달한다.

3. 2번 장교는 majority(v,v,x) = v를 값으로 사용하고, 이는 올바른 값이다.

위 경우는 IC1 & IC2를 둘다 만족함으로 OM은 비잔틴 장군 문제의 해답이 된다.

임의의 m에 대하여 OM(m) 증명하기

우리의 원래 목표 우리는 OM(m)이 장군이 최소 3m+1명에 배신자 m명인 경우의 비잔틴 장군 문제를 해결할 수 있음을 보일 것이다. 을 임의의 m에 대하여 보이자.

Lemma 1

위 내용을 증명하기 전에 먼저 보조정리 Lemma 1을 먼저 보이자. Lemma 1은 다음과 같다.

모든 임의의 m과 k에 대하여 장군이 2k+m명보다 많고 최대 k명의 배신자가 있으면,
알고리즘 OM(m)은 IC2를 만족한다.

귀납적 증명

IC2는 사령관이 충실한 경우만 해당하기 때문에 사령관이 배신한 경우는 고려하지 않아도 된다.

1. OM(0)

   앞서 언급된 OM(0)의 정의에 의하여 모든 충실한 장교들은 사령관이 보낸 값을 사용한다.

2. m-1인 경우에 위 보조정리 1을 만족할 때, m인 경우에 이를 증명하자

   다시 OM(m)의 정의를 생각해보자. OM(m)의 첫번째 스텝에서 충실한 사령관은 n-1명의 장교에게 값 v를 전달한다. 두번째 스텝에서 각 충실한 장교들은 OM(m-1)에서 n-1명의 장군(사령관 포함)들에게 첫번째 스텝에서 전달받은 값을 전달한다.

   가정에 의하여 $n > 2k+m$ 이고, 이는 $n-1 > 2k+ (m-1)$ 이다. 우리는 m-1에 대하여 보조정리 1이 성립한다고 가정하였기 때문에, $n-1 > 2k+ (m-1)$에서 알고리즘 OM(m-1)은 IC2를 만족한다. 즉, 모든 장교는 j번째 장교로부터 v(j) = v를 전달받게 된다. 최대 k명의 배신자가 존재함으로 $n-1>2k+(m-1)\ge 2k$ 이므로 과반수 이상의 장교들은 충실하다. 즉, 모든 충실한 장교들은 n-1의 과반수 이상의 v(i)=v를 전달받았고, majority(v(1),v(2),...v(n)) = v가 된다. 모든 충실한 장교들이 사령관이 전달한 값 v를 사용하기에 OM(m)은 IC2를 만족한다.

Theorem 1

이제 본격적으로 원래 증명하려 하였던 정리를 증명해보자. Theorem 1은 다음과 같다.

모든 임의의 m에 대하여 장군이 3m명보다 많고, 최대 m명의 배신자가 있을 때 OM(m)은 IC1과 IC2를 만족한다.

귀납적 증명

1. OM(0)
   배신자가 없을 때, OM(0)은 IC1과 IC2를 만족한다.

2. OM(m-1)가 해당 정리를 만족할 때, OM(m)을 보이자.

   • 사령관이 충실할 때
     보조정리 1에서 k에 m을 대입하면 OM(m)은 IC2를 만족한다. 앞서 언급하였듯이, 사령관이 충실한 경우에 IC1는 IC2가 만족되면 자연스럽게 충족되기 때문에 증명은 끝난다.

   • 사령관이 배신하였을 때
     사령관이 배신하였으므로, 최소 3m-1명의 장교 중에서는 최대 m-1명의 배신자가 존재한다. OM(m-1)가 Theorem 1을 만족함으로 $3m-1 > 3(m-1)$일 때, OM(m-1)은 IC1과 IC2를 만족한다. 그렇다면, IC2에 의하여 모든 충실한 장교들은 모든 j에 대하여 동일한 v(j)값을 전달 받는다. 결국 모든 충실한 장교들은 동일한 v(1),v(2),...v(n-1)값을 받고, 이는 동일한 majority(v(1),v(2),...v(n-1))로 이어진다. 결국 모든 충실한 장군들은 같은 값을 사용하기에 IC1이 만족된다.