이 포스트는 The Byzantine Generals Problem - Leslie Lamport을 읽고 저만의 방식으로 정리한 글입니다.
이 떄까지 우리는 장군들이 서로 다른 장군들에게 자유롭게 직접적으로 메시지를 보낼 수 있다고 가정해왔다. 이번에는 이 가정을 없애고, 대신에 물리적 장애물이 존재하여서 보낼 수 있는 장군에 제한이 있는 상황을 고려해보자.
그래프
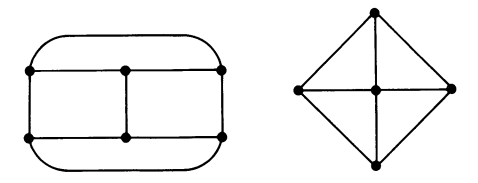
꼭짓점이 장군이고, 선으로 이어져 있는 장군끼리는 서로 메시지를 전할 수 있다.
용어들
-
이웃(neighbors)
선으로 이어져 있는 두 장군을 이웃 관계라 한다. -
p 정규 그래프(p-regular graph)
각 꼭짓점이 동일한 p개의 갯수에 이웃을 가지는 그래프이다.
왼쪽 그래프는 3-정규 그래프이고, 오른쪽 그래프는 중앙의 꼭짓점이 4개의 이웃한 점을 가져서 정규 그래프가 아니다.
OM(m) & 3m-정규 그래프
앞서 살펴본 OM(m) 알고리즘을 확장하여서 우리는 이 알고리즘을 통해 장군들의 그래프가 3m-정규 그래프이고, 최대 배신자가 m명인 비잔틴 장군의 문제를 해결할 수 있다. 증명은 생략한다.
믿을 수 있는 시스템
믿을 수 있는 시스템을 구축하기 위해서는 하나의 결과를 위해 서로 다른 프로세서를 이용해서 그 값들 중에 과반수인 값을 고르면 된다. 하지만 이와 같은 과정을 위해서는 다음과 같은 조건을 먼저 만족해야 한다.
만족해야하는 조건들
-
모든 이상 없는(nonfaulty) 프로세서는 같은 인풋값을 사용해야한다. 그래야 프로세서들이 같은 아웃풋을 도출하기 때문이다.
-
만약 인풋을 내는 장치에 이상이 없다면, 모든 이상 없는 프로세서는 해당 값을 인풋으로 사용해야 한다. 그래야 올바른 아웃풋을 내기 때문이다.
앞서 우리가 비잔틴 장군 문제를 해결할 때 만족해야 하는 IC1 & IC2와 동일하다.
- 사령관 <-> 인풋을 내는 장치
- 장교 <-> 프로세서
- 이상 없는 <-> 충실한
가정들
앞서 OM & SM 알고리즘에서 당연시 했던 가정 A1 ~A4 역시 실제 시스템을 구축할 때는 당연시 할 수 없다.
-
A1; 모든 이상없는 프로세서가 보낸 메시지는 올바르게 전달되어야 한다.
실제 시스템에서는 커뮤니케이션이 실패할 수 있다. -
A2; 프로세서는 해당 메시지를 누가 보냈는지 알 수 있다.
이 말은 이상이 있는 프로세서가 이상 없는 프로세서를 흉내내지 못한다는 이야기이다. -
A3; 메시지의 부재는 탐지 가능하다.
메시지가 도착하는 시간의 제한을 걸면 메시지의 부재를 탐지 가능하다. 만약에 해당 시간 제한보다 늦게 프로세서가 보낸다면, 우리는 그 프로세서를 이상이 있다고(faulty) 간주한다. -
A4; 이상 없는 프로세서들이 자신의 메시지를 사인하고, 다른 프로세서들은 이 사인을 위조하지 못한다.
사인이라는 것은 데이터이기 때문에 A4를 완전히 100% 보장하는 것은 불가능하다. 하지만, 암호학을 적용시킨다면, A4가 보장되지 않을 확률을 거의 0에 가깝게 만들 수 있다.
결론
이 논문에서는 여러가지 가정과 상황에서 비잔틴 장군 문제의 해결을 다루고 있다. 해당 알고리즘들은 모두 시간과 메시지양의 측면에서 매우 비싸다.
