Binary Search Tree

트리 구조는 편리한 구조를 보여주는 것 뿐만 아니라 효율적인 탐색을 위해서 사용 된다.

많은 트리 모양 중 이진 트리와 이진 탐색 트리는 효율적인 탐색을 위해 사용 된다.

이진 트리란?

이진 트리는 노드가 최대 두 개의 자식 노드를 가지는 트리이다.

이진 트리의 특징은 다음과 같다.

• 노드의 최대 차수는 2이다.
• 이진 트리는 왼쪽 자식 노드와 오른쪽 자식 노드를 가진다.
• 이진 트리는 왼쪽 자식 노드가 부모 노드보다 작고 오른쪽 자식 노드가 부모 노드보다 크다.
• 이진 트리는 왼쪽 자식 노드와 오른쪽 자식 노드가 모두 이진 트리이다.
• 이진 트리는 루트 노드가 존재한다.
• 이진 트리는 노드가 없는 곳에는 NULL을 표시한다.

이진 트리는 자료의 삽입 , 삭제 방식에 따라서 다음과 같이 분류 할 수 있다.

• 완전 이진 트리
• 포화 이진 트리
• 정 이진 트리
  

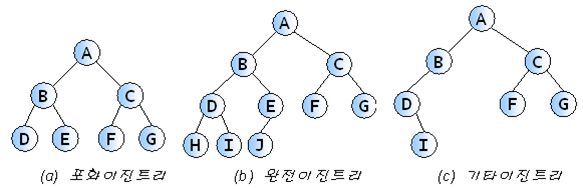
완전 이진 트리

완전 이진 트리는 노드가 왼쪽에서 오른쪽으로 차례대로 채워진 이진 트리이다.

완전 이진 트리는 노드가 없는 곳에는 NULL을 표시한다.

포화 이진 트리

포화 이진 트리는 모든 레벨에 노드가 꽉 차 있는 이진 트리이다.

포화 이진 트리는 노드의 개수가 2^k - 1개이다. (k == depth)

정 이진 트리

정 이진 트리는 모든 노드가 0개 또는 2개의 자식 노드를 가지는 이진 트리이다.

정 이진 트리는 노드가 없는 곳에는 NULL을 표시한다.

이진 탐색 트리란?

이진 탐색 트리는 이진 트리의 일종으로 이진 트리의 특징을 모두 가지고 있다.

이진 탐색 트리는 다음과 같은 특징을 가진다.

• 이진 탐색 트리는 왼쪽 자식 노드가 부모 노드보다 작고 오른쪽 자식 노드가 부모 노드보다 크다.
  • left Node < Parent Node < right Node
• 이진 탐색 트리는 왼쪽 자식 노드와 오른쪽 자식 노드가 모두 이진 탐색 트리이다.
• 이진 탐색 트리는 루트 노드가 존재한다.
• 이진 탐색 트리는 노드가 없는 곳에는 NULL을 표시한다.

Tree Traversal

트리의 순회는 트리의 모든 노드를 한 번씩 방문하는 것을 말한다.

트리의 순회는 다음과 같은 방법으로 구분 할 수 있다.

• 전위 순회 (Preorder Traversal)

• 중위 순회 (Inorder Traversal)

• 후위 순회 (Postorder Traversal)

  이 포스팅에서는 전위 순회, 중위 순회, 후위 순회에 대해서 알아보겠다.

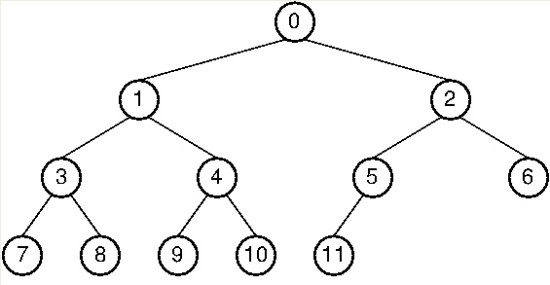
전위 순회 (Preorder Traversal)

전위 순회는 루트 노드를 먼저 방문하고
왼쪽 자식 노드를 방문한 후 오른쪽 자식 노드를 방문하는 순회 방법이다.

전위 순회는 다음과 같은 순서로 노드를 방문한다.

1. 루트 노드를 방문한다.
2. 왼쪽 자식 노드를 방문한다.
3. 왼쪽 자식 노드의 왼쪽 자식 노드를 방문한다.
4. 최하위 일 경우 노드일 경우 왼쪽 자식 노드의 오른쪽 자식 노드를 방문한다.
5. 오른쪽 자식 노드의 왼쪽 자식 노드를 방문한다.
6. 오른쪽 자식 노드의 오른쪽 자식 노드를 방문한다.
7. 왼쪽 자식 노드의 왼쪽 자식 노드의 왼쪽 자식 노드를 방문한다.
   ...

중위 순회 (Inorder Traversal)

중위 순회는 왼쪽 자식 노드를 먼저 방문하고
루트 노드를 방문한 후 오른쪽 자식 노드를 방문하는 순회 방법이다.

중위 순회는 다음과 같은 순서로 노드를 방문한다.

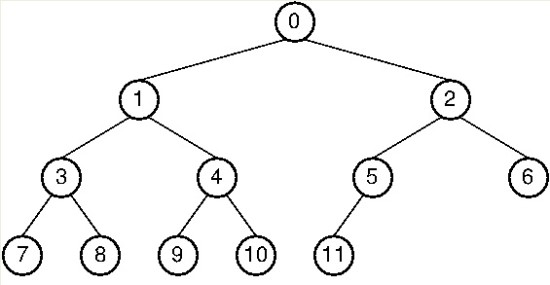
7 -> 3 -> 8 -> 1 -> 9 -> 4 -> 10 -> 0 -> 11 -> 5 -> 2 -> 6

후위 순회 (Postorder Traversal)

후위 순회는 하위 트리를 모두 방문 후 루트 노드를 방문하는 순회 방법이다.

후위 순회는 다음과 같은 순서로 노드를 방문한다.

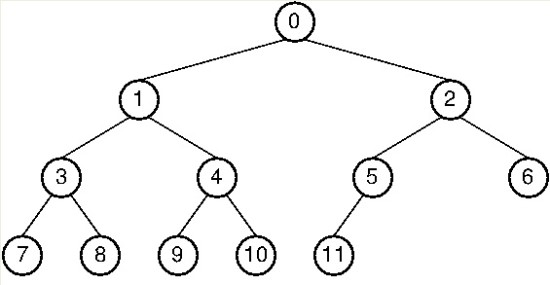
7 -> 8 -> 3 -> 9 -> 10 -> 4 -> 1 -> 11 -> 5 -> 6 -> 2 -> 0

즉, 간단하게 말해서 후위 순회는 왼쪽 자식 -> 오른쪽 자식 -> 부모 노드 -> 자식 노드의 같은 계층 노드 순으로 방문한다.