Divide and Conquer

분할 정복(Divde and Conquer)란?

• 문제를 재귀적으로 분할해서 해를 구하고, 그 해들을 결합해서 원래의 해를 구하는 알고리즘

  1. 문제를 divde하면서 더 이상 나눌 수 없는 degenerate case가 나올 때까지 나눔
  2. degenerate case의 문제를 conquer하면서 해를 구함
  3. 해를 구한 case들을 combine하면서 원래의 해를 구함

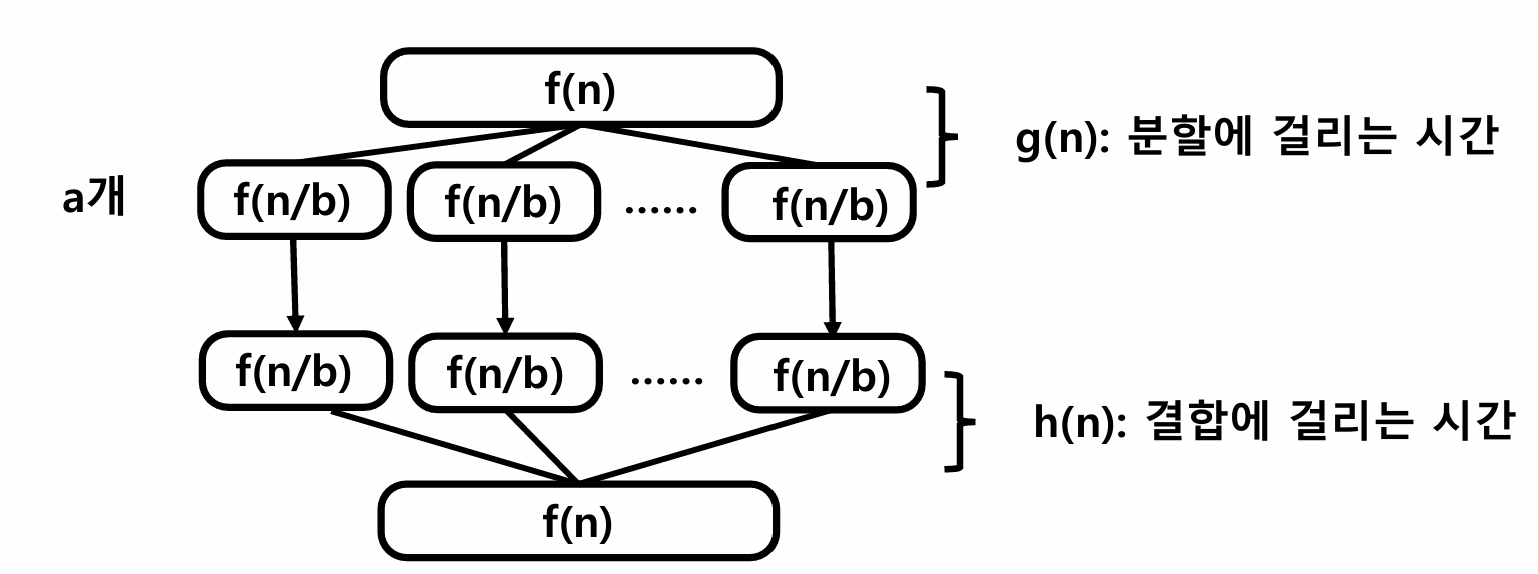
• 분할 정복의 기본 구조

dnc(int s, int e) {
	//1
    degenerate case -> conquer
    //2 
    divde
    //3
    combine
}

이처럼 분할 정복에는 3가지 요소가 필요
이를 식으로 표현하면 f(n) = a * f(n/b) + g(n) +h(n)

예시

• 분할 정복의 시간 복잡도

  • T(n) = a * T(n/b) + O(n^d)

  • 이 점화식을 풀기 위해서 마스터 정리(master theorem)을 사용한다.

    마스터 정리
    O (n^d), if d > log(b)a
    O(n^d*log(n)), if d = log(b)a = T(n)
    O(n^log(b)a), if d < log(b)a

  • 예) merge sort
    T(n) = 2 T(n/2) + O(n) 일때,
    a = 2, b = 2, d = 1 = log(b)a = log(2)2임으로
    T(n) = O(n1*log(n)) = O(nlog(n))이다.

dnc 알고리즘

binary search

• 정렬된 배열에서 특정 key가 어디있는지 찾는 알고리즘
• 배열을 절반씩 나누면서 key값이 위치를 찾는다.

binary_search(int a, int e) {
	if(s == e) // 1. degenate case, g(1) 
    	reutenr (arr[s] == key) ? s : -1;
    m = (a + b) /2;
    
    if(arr[m] == key) // divde
    	return m;
    else if(arr[m] > key)
    	binary_search(m+1, e); // T(n/2)
    else 
    	binary_search(a, m-1);
    
    // combinie X  h(n) = 0
}

• 배열을 나누면서 나눌 수 가 없는 s와 e의 값이 동일해 질 때까지 나눈다.
• 시간복잡도는 T(n) = 1 T(n/2) + O(1)
  a = 1, b = 2, d = 0이고 , d = log(2)1이니,
  T(n) = O(n^0log(n)) = O(log(n))이다.