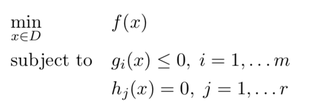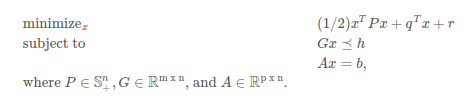• 본 글은 인공지능 및 기계학습 개론Ⅰ를 정리한 글입니다.

5.2 Maximizing the Margin

Margin을 최대화하기 위해 먼저 Margin Distance를 계산한다.

Margin Distance 계산하기

Margin Distance를 구하기 위해서 아래의 3개의 가정을 이용한다.

1. $f(\mathbf{x}) = w \cdot \mathbf{x} + b$
2. Decision Boundary 위에 있는 점에 대하여 $f(\mathbf{x}) = w \cdot \mathbf{x} + b = 0$이다.
3. positive case의 벡터인 $\mathbf{x}$에 대하여 $f(\mathbf{x}) = w \cdot \mathbf{x} + b = a, a>0$이다.

(여기서 $w$는 초평면의 법선 벡터이고, $\mathbf{x}$는 실수 벡터이다. $\mathbf{y_i}$는 $\mathbf{x}$가 어떤 클래스에 속해 있는지를 나타내는 값으로 양수 혹은 음수의 값을 갖는다. (positive case를 1, negative case를 -1로 가정할 수도 있음) 가정 3에서의 $\mathbf{x}$은 positive case $\mathbf{y_i}$의 데이터 중 초평면과 가장 가까운 서포트 벡터이다. 예를 들면 위의 그림에서 (3,0)일 것이다. a: Decision Boundary(초록색 선)와 positive front line(파란색 선)과의 거리)

임의의 점 $\mathbf{x}$에서 Decision Boundary로 수선의 발을 내린 점을 $\mathbf{x_p}$라고 하자. $\mathbf{x_p}$를 벡터 $w$의 방향으로 r만큼 간 벡터가 $\mathbf{x}$이다. 이를 식으로 쓰면 아래와 같다.

$x = x_p +r \frac {w}{\lVert w \rVert}, f(x_p) = 0$

이제 positive case인 점 a에 대해서 Margin Distance r을 계산해보자.

$f(x)= w \cdot x + b = w(x_p + r\frac {w}{\lVert w \rVert}) + b = wx_p + b + r\frac {w \cdot w}{\lVert w \rVert} = f(x_p) + r{\lVert w \rVert}= r{\lVert w \rVert}=a$

따라서 Margin Distance는 $r=\frac {f(x)}{\lVert w \rVert}$이다.

Maximizing the Margin

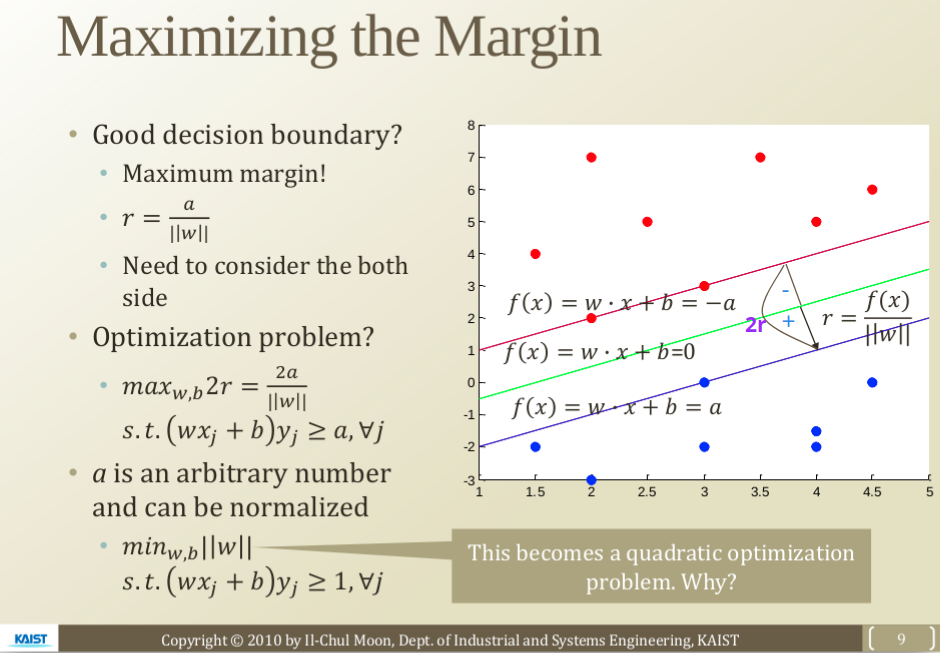
• 좋은 Decision Boundary
  margin이 최대가 되도록 하는 Boundary

Decision Boundary는 $f(\mathbf{x}) = w \cdot \mathbf{x} + b$이다. 그런데 bias term b는 방향 w만 찾으면 쉽게 구할 수 있으므로 좋은 Decision Boundary를 구하려면 우선 w의 최적화(optimization)만 찾으면 된다.

$r=\frac {f(x)}{\lVert w \rVert}$이므로 w를 최적화하기 위해서는 Margin Distance를 최적화하면 된다. 그리고 Margin Distance를 최적화하기 위해서는 Margin Distance의 양쪽 방향, 즉 positive case와 negative case 모두 고려해야 한다.

따라서 2r(r: Margin Distance)을 최대화하는 방향 벡터 w, bias term b를 찾으면 된다.

$max_{w,b}2r = \frac {2a}{\lVert w \rVert}$

(a는 임의의 양수이며 모든 j에 대하여 $(wx_j+b)y_j \geqslant a$이다. $x_i$: 훈련데이터의 input features,$y_i$: labels, j: 데이터의 각 instance)
(여기서 $(wx_j+b)y_j$는 5.1에서 언급한 confidence level이다.)

위의 식에서 w가 분모에 있어 구하기 까다로우므로 w를 분자에 있도록 하는 식으로 바꿔보자. a는 임의의 양수이므로 a=1이라 하고 정규화할 수 있으므로 2->1로 바꿀 수 있다.

$min_{w,b}2r ={\lVert w \rVert}$
(모든 j에 대하여 $(wx_j+b)y_j \geqslant 1$)

위의 식이 Margin Distance를 최적화하는 식이고, 최적화 문제(optimization problem)*이다.

그런데 $\lVert w \rVert = \sqrt{w_1^2+w_2^2}$이므로 이 문제는 quadratic optimization problem**로 치환된다. 이 문제는 quadratic programming을 이용해 최적화를 수행할 수 있다. 여기서 quadratic programming을 설명하기에는 복잡하므로 다루지 않지만 자주 사용되므로 찾아보는 것이 좋다.

가장 쉽게 이 문제를 해결할 수 있는 방법은 R이나 Matlab의 quadratic programming optimizer를 사용해 w를 예측하는 것이고, 강의에서는 Matlab을 사용해 w를 예측해본다.

• 위의 내용이 이해가 안 간다면 위키백과의 선형 SVM를 참조하면 된다.

• 참고: SVM을 이용한 Decision Boundary 구현

* 최적화 문제(Optimization problems)
여러 개의 선택가능한 후보 중에서 최적의 해(Optimal value) 또는 최적의 해에 근접한 값을 찾는 문제이다. 수학적 최적화 문제는 아래와 같은 식으로 표현된다.

• 참고: https://wikidocs.net/17203

**Quadratic Program(QP)
목적함수(objective function)가 이차식 (convex quadratic)이고, 제약함수(constraint functions)가 모두 affine인 convex optimization problem이다. General quadratic program은 다음과 같은 형태로 표현될 수 있다.

• 참고: https://wikidocs.net/17852

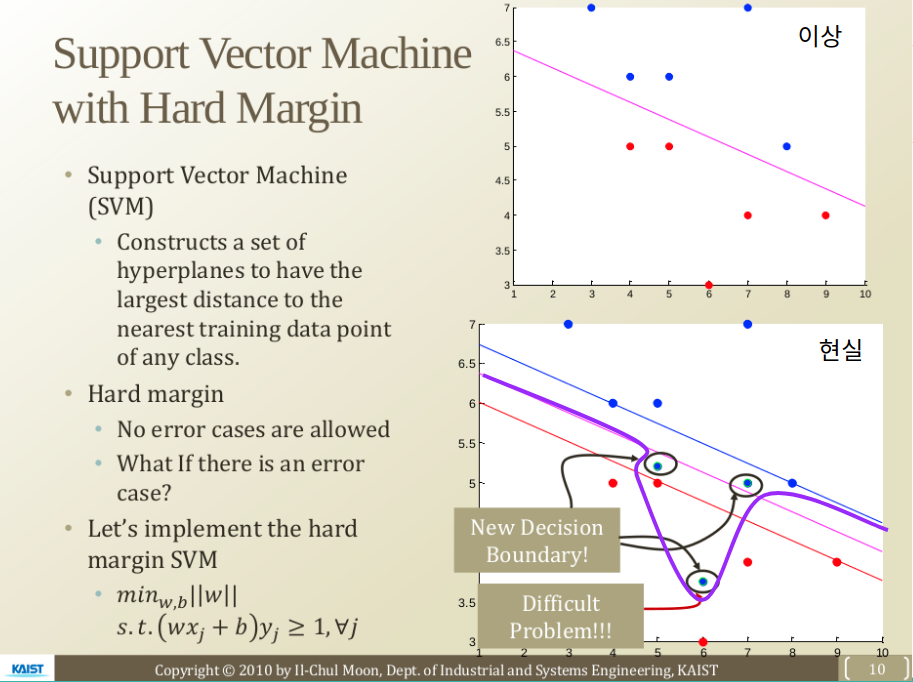
Support Vector Machine with Hard Magin

• SVM: 서포트 벡터 머신은 어떤 분류된 점에 대해서 가장 가까운 학습 데이터와 가장 먼 거리를 가지는 초평면들의 집합으로 구성되어 있다.

• quadratic programming이 항상 좋은 것인가?

  • feasible solution: 최적화할 때, 조건에 맞는 해(w)를 찾을 수 있다.
  • infeasible solution: 최적화할 때, 조건에 맞는 해(w)를 찾을 수 없다.

• 만약 w를 찾지 못한다면 어떻게 될까?
  아래쪽 그림과 같이 파란색 점 때문에 주어진 조건을 만족하지 못하는 경우는 Decision Boundary를 찾을 수 없다.
  

그런데 문제는 현실에서는 Linear Decision Boundary로 케이스가 정확하게 분류되지 않는다는 점이다.

• Hard Margin
  지금까지는 Hard Margin 방법을 살펴보았다. Hard Margin은 어떤 error를 허용하지 않으면서 Decision Boundary로 두 클래스를 나누는 방법이다. 그러나 현실에서는 error가 많아서 Hard Margin SVM을 사용하기 어렵다. 따라서 Hard Margin SVM을 수정해야 한다.

• Hard Margin SVM을 수정하는 2가지 방식

1. Soft Margin SVM
   Linear Decision Boundary를 사용하지만 일부의 error를 인정한다. (다음 시간에 배울 것)

2. Hard Margin SVM with Kernel Trick
   Decision Boundary를 선형이 아닌 곡선으로 만들어 Hard Margin을 만든다. (다음 다음 시간에 배울 것)