목차
- 이진 탐색 트리
- 최적 이진 탐색 트리
이진 탐색 트리
최적 이진 트리를 알기 위해서는 이진 탐색 트리를 이해해야 한다.
이진 탐색 트리의 규칙 및 특징을 먼저 살펴보자
- 이진 트리이다
- 왼쪽 자식 노드의 값은 자신의 값보다 작아야 한다
- 오른쪽 자식 노드의 값은 자신의 값보다 커야 한다
- 서브 트리는 BST
- 값이 중복되는 노드는 없다
이진 탐색 트리의 예시를 그림으로 보면 다음과 같다
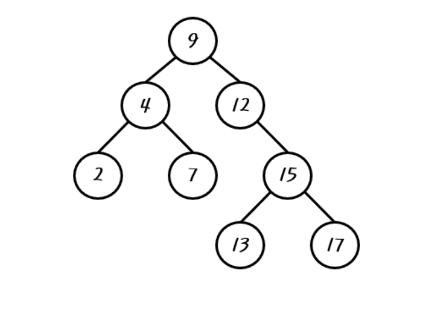
이진 탐색 트리에서 값의 검색은 어떻게 할까? 우리는 이진 탐색 트리의 특성을 다시 한번 살펴볼 필요가 있다.
“왼쪽 자식 노드의 값은 자신의 값보다 작으며, 오른쪽 자식 노드의 값은 자신의 값보다 크다”
따라서 탐색하고자 하는 값이 현재 있는 노드의 값보다 크다면 오른쪽 노드로 작다면 왼쪽 노드로 이동하면 된다.
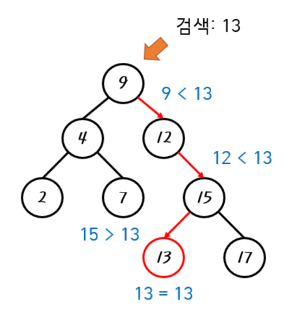
우리는 이를 재귀 함수로 쉽게 구현할 수 있다.
public static void binary_search(Node self, int value){
if(value < self.data){
if(self.left == null)
System.out.println(“Not Found”);
else binary_search(self.left, value);
}
else if(value > self.data){
if(self.right == null)
System.out.println(“Not Found”);
else binary_search(self.right, value);
}
else if(value == self.data){
System.out.println(“Found!”);
}이진 탐색 트리에서의 노드 삽입하는 방법은 검색하는 방법과 크게 다르지 않다.
삽입에는 두 가지 경우의 수가 존재한다
- 이미 값이 존재하는 경우
- 값이 존재하지 않는 경우
이미 값이 존재하는 경우는 중복적으로 값을 삽입할 수 없기에 예외처리를 해준다. 값이 존재하지 않는 경우는 검색하는 것과 같이 노드를 타고 내려가다가 마지막에 도달한 노드에 추가해 준다. 이 때 값이 작으면 왼쪽, 크면 오른쪽 노드에 삽입한다.
public static void insert_node(self, value){
if(value < self.data){
if(self.left == null)
self.left = new Node(value);
else insert_node(self.left, value);
}
else if(value > self.data){
if(self.right == null)
self.right = new Node(value);
else insert_node(self.right, value);
}
else if(value == self.data)
System.out.println(“Exception”);
}이진 탐색 트리에서의 노드 삭제는 조금 더 복잡하다. 왜냐하면 고려해야할 경우의 수가 증가했기 때문이다. 우리는 총 세개의 경우의 수를 고려해야한다.
- leaf 노드를 삭제하는 경우
- 자식 노드가 하나일 경우
- 자식 노드가 두개 일 경우
(미완)
최적 이진 탐색 트리
이제 최적 이진 탐색 트리를 살펴보자.
노드 안에 들어 있는 데이터는 숫자가 될 수도 있지만 문자열 혹은 다른 데이터가 들어갈 수 있다. 문자열이 들어갔다고 가정했을 때 우리가 크다 작다를 비교할 수 있는 기준은 알파벳의 순서다.
이진 트리는 같은 데이터 셋을 가지고 다른 모양을 만들 수 있다.
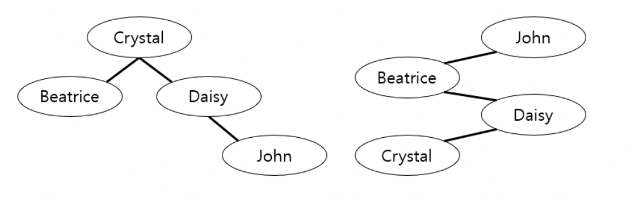
두 BST의 차이는 무엇일까? 어떤 특정 문자열을 탐색하기 위해 호출하는 함수의 횟수가 다르다. 예를 들어, ‘Crystal’ 을 검색한다 했을 때, 왼쪽 BST의 경우 한번에, 오른쪽 BST의 경우 세 번을 더 내려가야 한다.
우리가 고려할 것은 단어 별로 검색 요청이 들어오는 빈도가 다르다는 것이다. 예를 들어 다음과 같이 가정해보자.
Crystal = 0.1 / Daisy = 0.2 / Beatrice = 0.3 / John = 0.4
BST의 평균 검색 시간은 검색 빈도 * 필요 탐색 횟수를 모두 더한 것이다.
따라서 왼쪽 BST와 오른쪽 BST의 평균 검색 시간은 각각 다음과 같다.
왼쪽: (0.1*1) + (0.2*2) + (0.3*2) + (0.4*3) = 2.3
오른쪽: (0.1*4) + (0.2*3) + (0.3*2) + (0.4*1) = 2.0오른쪽 BST가 효율이 더 좋다는 것을 알 수 있다.
따라서 단어들이 주어졌을 때 만들 수 있는 가장 효율적인 트리를 최적 이진 트리라고 부른다.
만약 우리가 무식하게 모든 경우의 수를 구한다면, 어떤 루트 노드를 제외한 나머지 노드를 배치하는 순서는 총 2^(n-1)이 된다.
따라서 우리는 Dynamic Programming을 활용 해야 한다.
BST의 특성상 어떤 BST의 왼쪽, 오른쪽 서브 트리가 최적 BST여야 해당 BST도 최적이다. 즉 최적의 원리가 성립한다.
이차원 배열 A에 각 서브 트리의 최적의 값을 저장한다고 했을 때, 우리는 다음과 같은 점화식을 도출할 수 있다.
즉 왼쪽 서브 트리 최적 + 오른쪽 서브 트리 최적 + K를 루트로 두는 총 경우의 수라고 할 수 있다.
루트 노드 탐색 시간이란?
루트 노드 탐색 시간이란?
탐색 시간은 원하는 키를 찾기까지 필요한 비교 횟수이다.
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scn = new Scanner(System.in);
int n = scn.nextInt();
int[] keys = new int[n];
for (int i = 0; i < n; i++) {
keys[i] = scn.nextInt();
}
int[] frequency = new int[n];
for (int i = 0; i < n; i++) {
frequency[i] = scn.nextInt();
}
optimalbst(keys, frequency, n);
}
private static void optimalbst(int[] keys, int[] frequency, int n) {
// make prefix sum of frequencies
int[] fsum = new int[n];
for (int i = 0; i < n; i++) {
if (i == 0) {
fsum[i] = frequency[i];
} else {
fsum[i] = frequency[i] + fsum[i - 1];
}
}
int[][] cost = new int[n][n];
for (int gap = 0; gap < n; gap++) {
int si = 0;
int ei = gap;
while (ei < n) {
if (gap == 0) {
// diagonal
cost[si][ei] = frequency[si];
} else if (gap == 1) {
int sum = fsum[ei];
if (si - 1 >= 0) {
sum -= fsum[si - 1];
}
cost[si][ei] = Math.min(cost[si][ei - 1], cost[si + 1][ei]) + sum;
} else {
cost[si][ei] = Integer.MAX_VALUE;
int sum = fsum[ei];
if (si - 1 >= 0) {
sum -= fsum[si - 1];
}
for (int i = si; i < ei - 1; i++) {
cost[si][ei] = Math.min(cost[si][i] + cost[i + 2][ei] + sum, cost[si][ei]);
}
cost[si][ei] = Math.min(Math.min(cost[si][ei - 1], cost[si + 1][ei]) + sum, cost[si][ei]);
}
si++;
ei++;
}
}
System.out.println(cost[0][n - 1]);
}
}