시작

그래프 이론에 이어 트리이론까지 왔는데, 트리 이론을 간단하게 설명하자면, 말그대로 나무에서 나온 이론이다. 나무의 가지를 보면 가지에 가지가 나고, 또 가지에 가지가 난다는 것을 알 수 있는데, 그 것을 뒤집으면 Computer에 나오는 트리와 똑같다고 볼 수 있다.
트리는 계층적 구조라고 볼 수 있는데, 이유는 그래프 처럼 여기저기 퍼져있는게 아닌, 층층히 쌓이는 구조여서 계층적 구조다. 그리고 트리는 기본적으로 "무방향 그래프" 즉 방향이 따로 없는 그래프로, 사이클이 없는 자료구조를 의미한다.

노드

그렇다면 트리에서 나오는 노드들이 뭔지 궁금할텐데 한번 그림을 그리면서 알아보자.

우선 이 그림은 트리의 모형으로, 동그란 모형이 노드라고 부르는 친구다.부모노드와 자식노드로 간단하게 나눌 수 있는데. 우선 어떻게 나누는지는 현실의 부모와 자식을 생각을 하면된다.

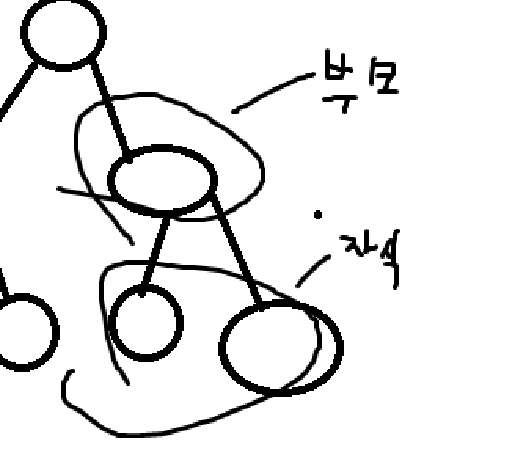
이런식으로 노드의 시작을 부모, 노드에서 뻗어나오는 노드는 자식으로 부르는데, 한 부모에서 뻗어나온 자식들끼리는 형제노드라고 부른다. 그렇 다면 트리에다가 임의의 수를 한번 부여해보자.

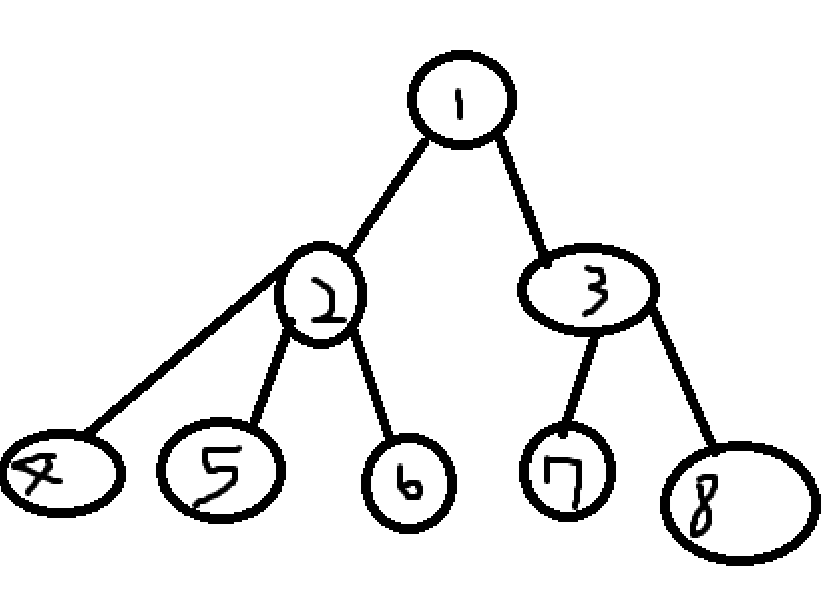
부여된 수로 한번 예시를 들어보자면, 2번의 자식노드는, 4,5,6번이라 할 수 있고, 7번의 부모 노드는 3번이다. 그렇다면 형제노드를 한번 말해보자면, 2번의 형제 노드는 3번이고 4번의 형제 노드는 5,6번이다. 그렇다면 6번의 형제 노드중 7, 8번도 형제노드가 될 수 있나? 그건 아니다. 형제노드가 되는 조건인 "같은 부모"가 아니기에 형제 노드가 될 수는 없다.

루트 노드

트리에서 최상위 노드를 "루트 노드"라고 부르는데, 루트라고 하면 진짜로 뿌리라고 이야기 하는데, 이유는 나무를 뒤집으면 맨 위의 부분이 뿌리기 때문에 루트 노드라고 부른다. 위에 그림으로 치면 1번은 루트 노드다.

리프 노드와 내부 노드

마지막으로 리프 노드와 내부 노드로도 나눌 수 있는데, 리프 노드는 자식이 없는 노드, 즉 자신 밑에 안 뻗어 나가는 노드를 이야기 하고 내부 노드는 리프 노드와 다르게 밑에 자식 노드가 있으면 내부 노드라고 한다.

이 그림에서의 내부노드는 1번과 2,3번이라 볼 수 있으며, 리프 노드는 4, 5, 6, 7, 8번이라고 할 수 있다.

정점과 간선의 개수

이 이야기는 아주 쉬울텐데 한번 해보자면, 정점의 개수는 "노드"의 개수다. 그렇다면, 간선의 개수는? 노드와 노드를 이어주는 선의 개수를 이야기하는 것. 한번 밑의 사진을 보면서 이야기를 해보자면.

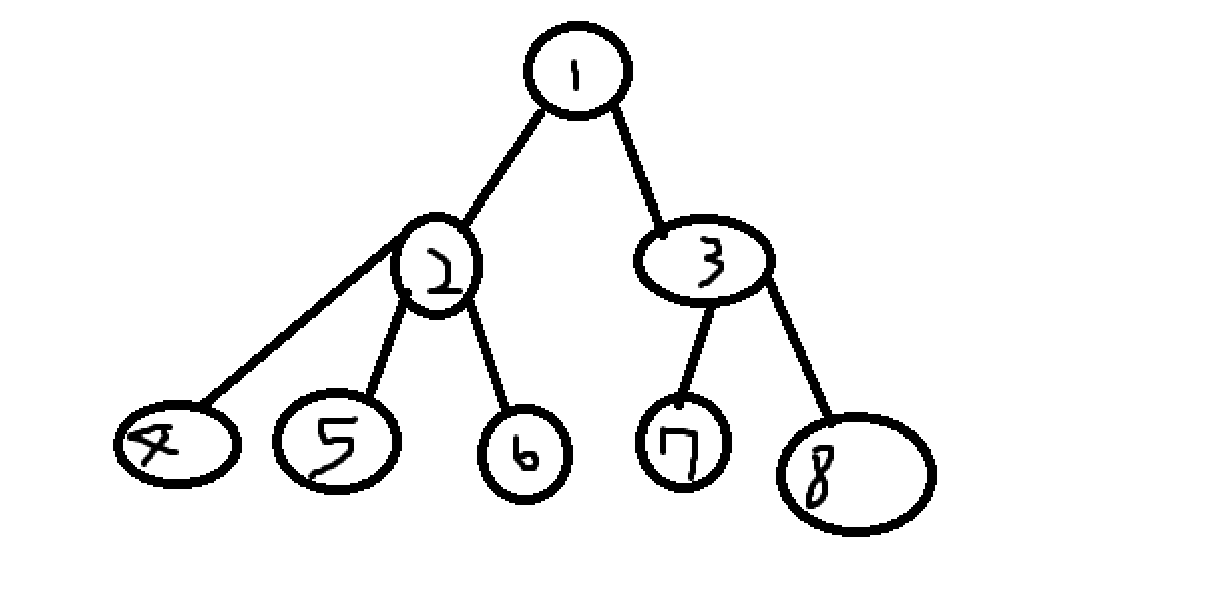
여기서의 노드의 개수 즉 정점의 개수는 8개라는 것을 알 수 있다. 그렇다면 간선의 개수는? 정점의 개수의 -1을 해주면 간선의 개수가 나오는데 8-1 =>7 글렇다면 간선의 개수는 7개인 것을 알 수 있다.(V-1 = E)

트리의 높이와 레벨

트리의 높이와 레벨을 알아볼텐데, 높이와 레벨은 같은 말이라 볼 수 있다. 그렇다면 이번에도 그림을 가지고 한번 레벨을 알아보자.

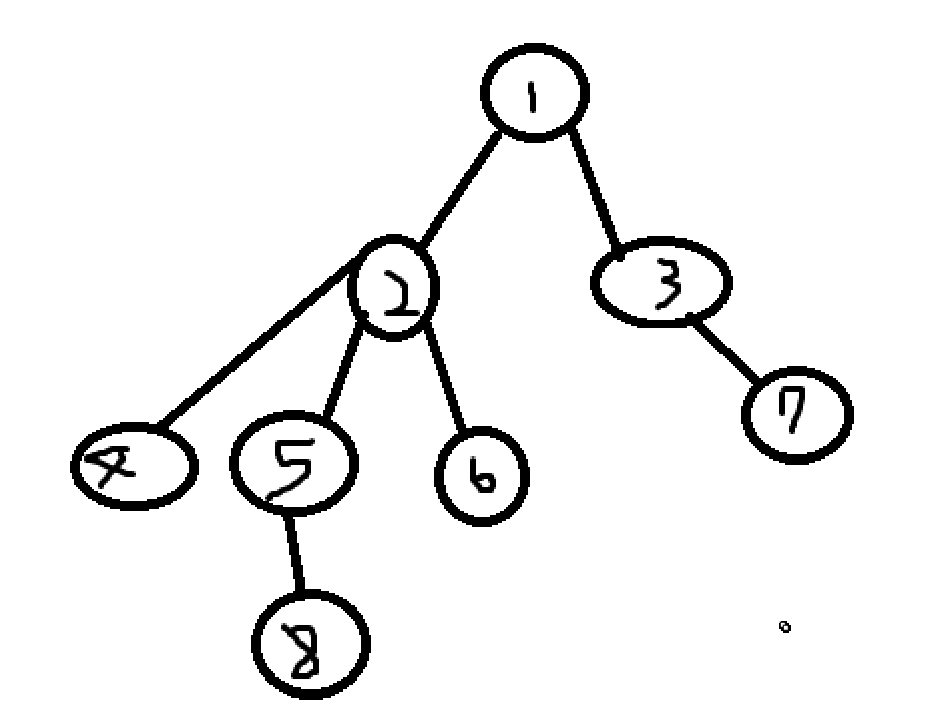
이 그림은 노드가 8개고, 간선의 개수는 7개다. 하지만 이 정보만 가지고 레벨을 알 수는 없는데, 맨 처음에서 이야기 했듯이, 트리는 계층적구조라고 했다. 그렇다면 층을 나눠서 본다면, 레벨을 알 수 있는데. 한번 레벨을 알아보자.

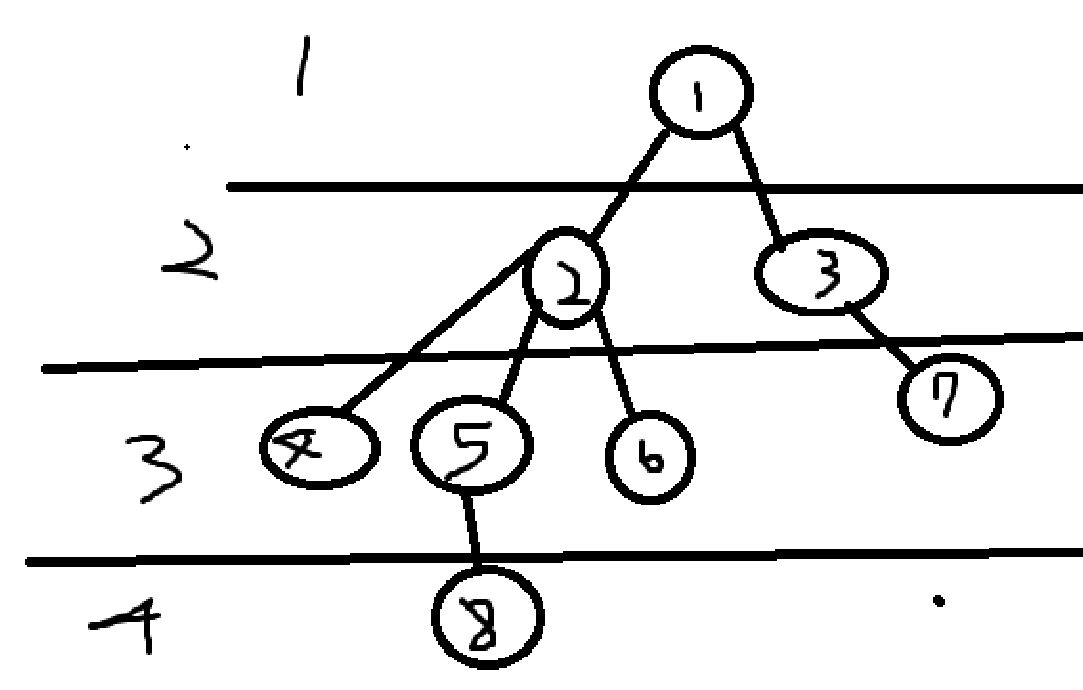
이런식으로 층을 나눈다면, 이 트리의 레벨은 4레벨이라는 것을 알 수 있다. 따라서 트리의 레벨은 트리의 층을 이야기 하는 것을 알 수 있는데, 깊이(Depth)도 이것과 관련이 있다.