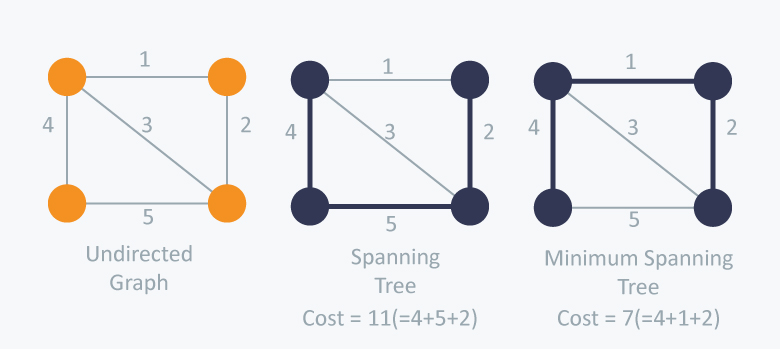
최소 신장 트리 (MST : Minimum Spanning Tree)

• 최소 신장 트리는 신장 트리 중에서 사용된 간선들의 가중치 합이 최소인 신장트리를 지칭함
• 각 간선의 가중치가 동일하지 않을 때 단순히 가장 적은 간선을 사용한다고 해서 최소 비용이 얻어지는 것은 아님
• MST는 간선에 가중치를 고려하여 최소 비용의 Spanning Tree를 선택하는 것
• 즉, 네트워크에 있는 모든 정점들을 가장 적은 수의 간선과 비용으로 연결하는 것

MST의 특징

1. 간선의 가중치의 합이 최소여야 한다.
2. n개의 정점을 가지는 그래프에 대해 반드시 (n-1)개의 간선만을 사용
3. 사이클이 포함되어서는 안된다.

MST의 사용 사례

• 통신망, 도로망, 유통망에서 길이, 구축 비용, 전송 시간 등을 최소로 구축하려는 경우

1. 도로건설 : 도시들을 모두 연결하면서 도로의 길이가 최소가 되도록 하는 문제
2. 전기 회로 : 단자들을 모두 연결하면서 전선의 길이가 가장 최소가 되도록 하는 문제
3. 통신 : 전화선의 길이가 최소가 되도록 전화 케이블 망을 구성하는 문제
4. 배관 : 파이프를 모두 연결하면서 파이프의 총 길이가 최소가 되도록 연결하는 문제

MST의 구현 방법

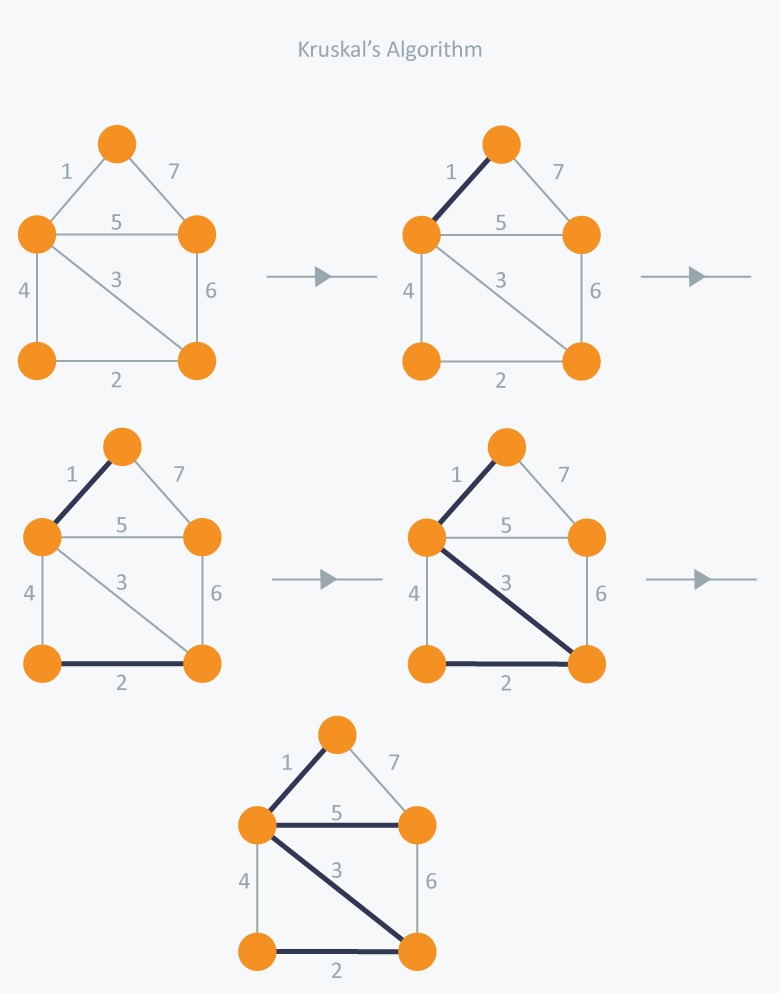
1. Kruskal's Algorithm

• 크루스칼 알고리즘은 신장트리에서 하나 하나 ㅇ간선을 더해가며 만드는 방법이다. 이 알고리즘은 각 반복마다 가장 적은 가중치를 가진 간선을 찾는 탐욕법과 비슷하다.

알고리즘 과정

1) 가중치를 기준으로 그래프 간선을 오름차순 섞는다.
2) 가장 큰 가중치가 나올때까지 작은 가중치 간선부터 MST 간선을 더해간다.
3) 사이클이 발생하지 않게 간선을 더한다.

• 이 과정은 DFS를 사용해 2개의 Vertice가 연결되어 있는지 안되어있는지 찾으면 된다.

크루스칼 알고리즘 코드 - Python

# 특정 원소가 속한 집합 찾기
def find(parent, x):
	if parent[x] == x:
    	return x
    parent[x] = find(parent, parent[x])
    return parent[x]
    
# 두 원소가 속한 집합 찾기
def union(parent, a, b):
	rootA = find(parent, a)
    rootB = find(parent, b)
    
    if rootA < rootB:
    	parent[rootB] = rootA
    else:
    	parent[rootA] = rootB


# 노드의 개수와 간선의 개수 입력받기
v, e = map(int, input().split())
parent = [0] * (v+1)

edges = []
result = 0

# 부모 테이블 상에서, 부모를 자기 자신으로 초기화
for i in range(1, v + 1):
	parent[i] = i

# 모든 간선에 대한 정보를 입력받기
for _ in range(e):
	a, b, cost = map(int, input().split())
    # 가중치를 오름차순으로 정렬하기 위해 튜블의 첫 번째 원소를 비용으로 설정
    edges.append((cost, a, b))

edges.sort()

for edge in edges:
	cost, a, b = edge
    # 사이클이 발생하지 않는 경우에만 집합에 포함된다.
    if find(parent, a) != find(parent, b):
    	union(parent, a, b)
        result += cost

print(result)

2. Prim Algorithm

• 프림 알고리즘은 시작 정점에서부터 출발하여 신장트리 집합을 단계적으로 확장해나가는 방법이다. 이 과정은 크루스칼과 다르게 신장트리에 정점을 더해가는 방식이다.

알고리즘 과정

1) 시작 단계에서는 시작 정점만 MST 집합에 포함된다.
2) 앞에서 만들어진 MST 집합에 인접한 정점들 중에서 최소 간선으로 연결된 정점을 선택하여 트리를 확장함 즉, 가장 낮은 가중치를 먼저 선택한다.
3. 트리가 N-1개의 간선을 가질 때까지 반복한다.

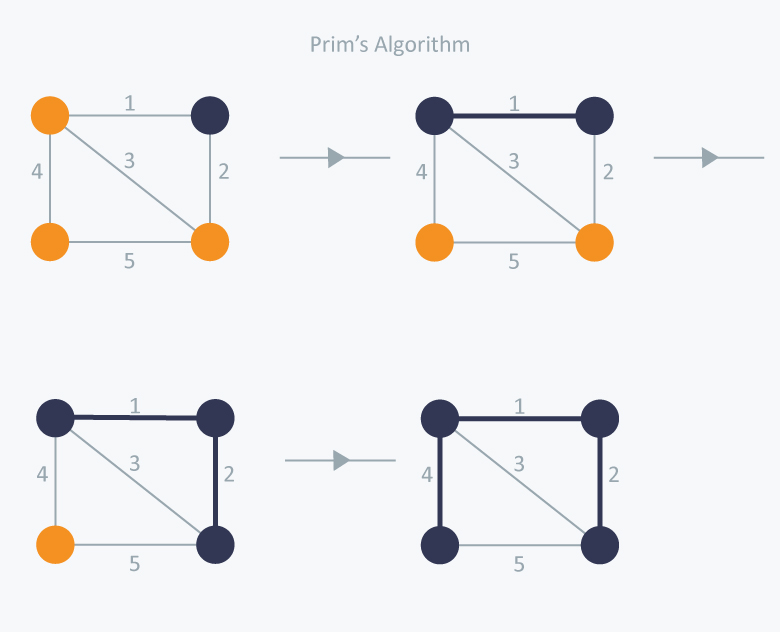
• 프림 알고리즘은 임의의 노드로 시작해 각 반복과정에서 우리가 이미 체크한 노드의 인접한 것에 또 마크를 한다.
• 탐욕법처럼, 프림 알고리즘은 가장 적은 간선을 선택하고 마크한다. 그래서 우리는 단순히 가중치를 기준으로 체크하게 된다.

1) Collections 라이브러리의 defaultdict 이용

# key에 대한 값을 지정하지 않았을 때 빈리스트로 초기화함
from collections import defaultdict

list_dict = defaultdict(list)
print(list_dict['key1'])

list_dict2 = dict()
print(list_dict2['key1'])

edges = [
    (7, 'A', 'B'), (5, 'A', 'D'),
    (8, 'B', 'C'), (9, 'B', 'D'), (7, 'B', 'E'),
    (5, 'C', 'E'),
    (15, 'D', 'E'), (6, 'D', 'F'),
    (8, 'E', 'F'), (9, 'E', 'G'),
    (11, 'F', 'G')
]

from collections import defaultdict
from heapq import *

def prim(first_node, edges):
	mst = []
    # 해당 노드에 해당 간선을 추가
    adjacent_edges = defaultdict(list)
    for weight, node1, node2 in edges:
    	adjacent_edges[node1].append((weight, node1, node2))
        adjacent_edges[node2].append((weight, node2m node1))
    
    # 처음 선택한 노드를 연결된 노드 집합에 삽입
    connected = set(first_node)
    # 선택된 노드에 연결된 간선을 간선 리스트에 삽입
    candidated_edge = adjacent_edges[first_node]
    # 오름 차순으로 정렬
    heapify(candidated_edge)
    
    while candidated_edge:
    	weight, node1, node2 = heappop(candidated_edge)
        # 사이클 있는지 확인 후 연결
        if node2 not in connected:
        	connected.add(node2)
            mst.append((weight, node1, node2))
            
            for edge in adjacent_edges[node2]:
            	if edge[2] not in connected:
                	heappush(candidated_edge, edge)
     
     return mst

2) 우선순위 큐를 통한 프림 알고리즘

• 간선이 나닌 노드를 중심으로 우선순위 큐를 만들어 풀어 나감
• 초기화 : 선택한 구조를 만든 후 Key값을 0으로 입력하고 나머지 노드는 무한대로 설정하고 큐에 넣음
• 가장 key값이 적은 노드를 pop으로 추출
• 해당 노드의 인접한 노드들에서 Key값과 가중치의 값을 비교하여 가중치 값이 작으면 해당 key값을 가중치 값으로 업데이트
• 업데이트 후 우선순위 큐에서 key값이 가장 작은 노드를 루트 노드로 올라오도록 해야 함
• heapdict 라이브러리 이용

from heapdict import heapdict

def prim(graph, first):
	mst = []
    keys = heapdict()
    previous = dict()
    total_weight = 0
    
    # 초기화
    for node in graph.keys()"
    	keys[node] = float('inf')
        previous[node] = None
    
    keys[first], previous[first] = 0, first
    
    while keys:
    	current_node, current_key = keys.popitem()
        mst.append([previous[current_node], current_node, current_key])
        total_weight += current_key
        for adjacent, weight in graph[current_node].items():
        	if adjacent in keys and weight < keys[adjacent]:
            	keys[adjacent] = weight
                previous[adjacent] = current_node
    return mst, total_weight
    
graph = {
    'A': {'B': 7, 'D': 5},
    'B': {'A': 7, 'D': 9, 'C': 8, 'E': 7},
    'C': {'B': 8, 'E': 5},
    'D': {'A': 5, 'B': 9, 'E': 15, 'F': 6},
    'E': {'B': 7, 'C': 5, 'F': 8, 'G': 9},
    'F': {'D': 6, 'E': 8, 'G': 11},
    'G': {'E': 9, 'F': 11}
}

mst, total_weight = prim(graph, 'A')
print(mst)
print(total_weight)