하노이 탑, 니 뭔데? 🤯

백준: 1914번 하노이 탑
GitHub: 풀이 코드

하노이의 탑은 작은 원반이 위에, 큰 원반이 아래에 위치하는 규칙을 지키면서 기둥 3개를 이용해서 원판을 옮기는 문제이다.

규칙을 발견해서 원판 갯수에 따른 경우의 수를 구하는 것은 쉽게 발견했었다. 하지만 그 옮기는 과정을 구하는 것은 하루종일 생각해봤는데도 떠오르지 않아서 책을 통해서 풀어보는 방법을 공부한 후에 직접 짜보았다.

move(int(input()),1,3)

# N : 원판의갯수 / x: 시작기둥 번호 / y: 도착기둥 번호
def move(N, x, y):
	if N > 1:
    	move(N-1, x, 6-(x+y))
    
    # print(N, x, y) # 원판 N을 x기둥에서 y기둥으로 옮겨줘
    print(x,y)
    
    if N > 1:
    	move(N-1, 6-(x+y), y)

재귀함수(recursive)를 이용해서 정말 코드는 간단하고, 어떻게 돌아가는 로직인지 다 이해는 했었지만, 남은 기둥 구하는 식(6-(x+y))을 어떻게 유추 해야 할 지가 어려웠다.

지금까지 내가 공부해 본 유추하는 방법이다.

우선 기둥은 3개이고, [1번기둥], [2번기둥], [3번기둥]으로 구분한다.
그래서 6 = 1번기둥 + 2번기둥 + 3번기둥 이며,
6 - x 기둥 - y 기둥 = 남은 기둥 번호 로 유추할 수 있다.

재귀함수로 어떻게 풀어야할까?

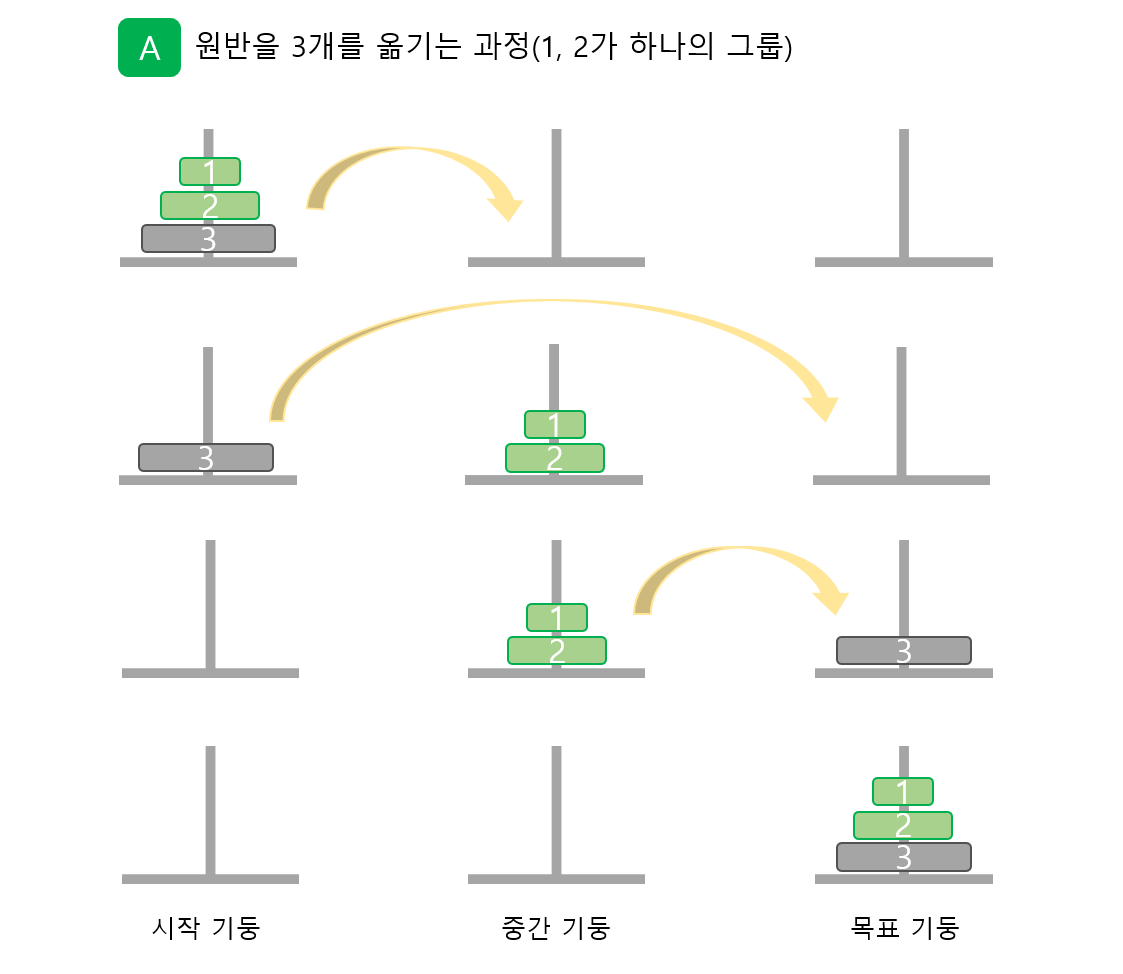
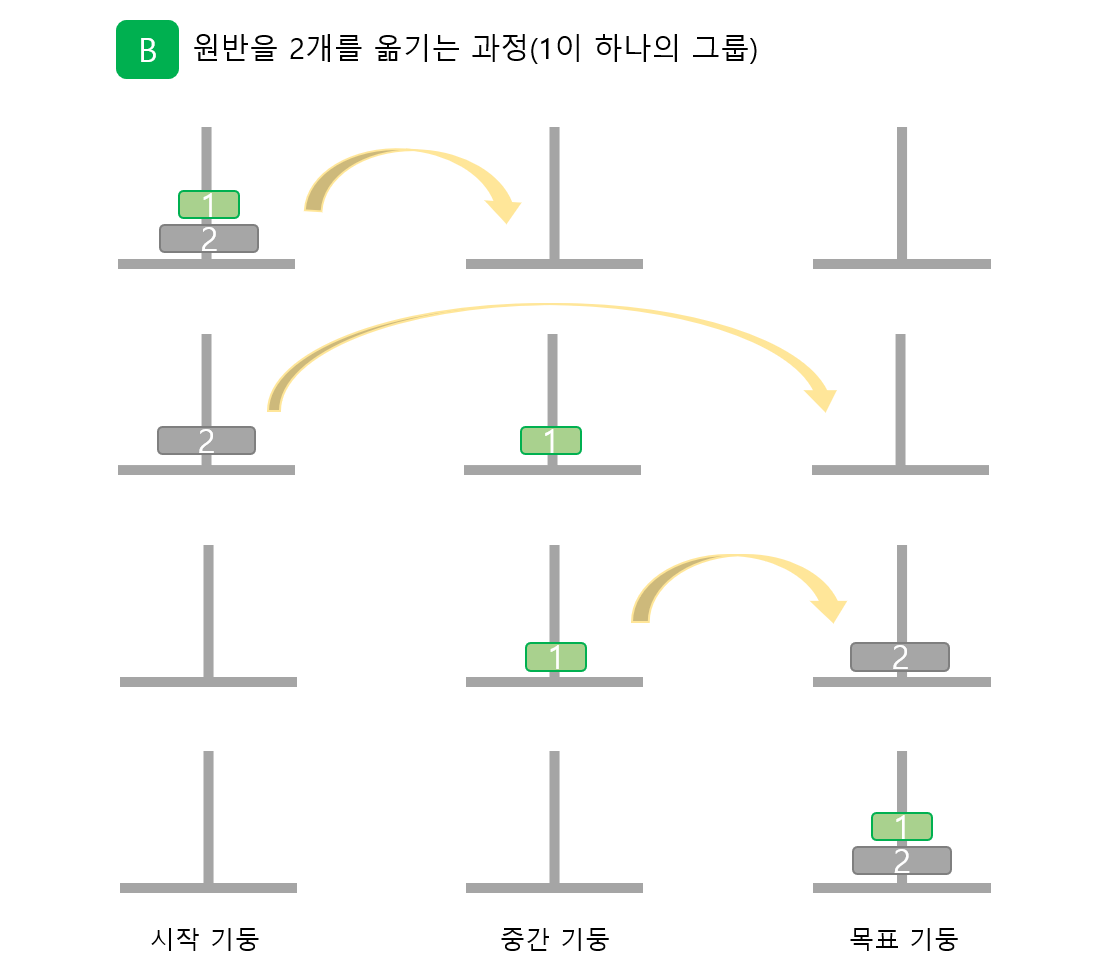
위의 두 과정을 보면 하노의 탑은 일련의 과정을 거칩니다.

하노이의 탑은 아래의 3과정을 거칩니다.
바닥 원반을 제외한 그룹(원반[1] ~ 원반[no - 1])을 시작 기둥에서 중간 기둥으로 옯깁니다.
바닥 원반 no를 시작 기둥에서 목표기둥으로 옮겼음을 출력합니다.
바닥 원반을 제외한 그룹(원반[1] ~ 원반[no ~ 1])을 중간 기둥에서 목표 기둥으로 옮깁니다.

예를 들어, 처음에 원판 5개를 1에서 3으로 옮겨야 된다고 생각해보면 쉽다. 이를 크게 3개의 작업을 쪼개어 보면,

1. 맨 밑판을 제외한 4개를 2에 옮긴다.
2. 맨 밑판을 3에 옮긴다.
3. 2에 쌓인 4개를 3에 옮긴다.

이 3개의 과정이 바로 solve, printf, solve의 의미이다.

✒️회고

하노이 탑은 정말 많이 들어봤는데, 이렇게 풀어본 적은 처음이였던 것 같다. 앞으로 많은 자료구조 문제들을 만나보게 될 꺼 같은데, 많이 걱정이 되기도 하고, 아직 공부를 많이 해야할 것 같다는 생각이 많이 들었다.

정글 오고 나서 처음으로 느껴보는 벽이 였는데, 이렇게 하는게 맞는 것인지 잘하고 있는 것인지 잘 모르겠다.

일단 화이팅!💪🙈