백준2225_합분해

• https://www.acmicpc.net/problem/1309
  

사자가 주어진 테이블에 조건에 맞게 배치할 수 있는 경우의 수를 묻는 문제이다.

⭐ my code

N = int(input())
dp = [1,1,1]

for n in range(1, N):
    for i in range(3):
        if i == 0 : dp[i] = sum(dp)
        else: dp[i] = dp[0] - dp[i]
print(sum(dp))

⭐ 문어 박사님 code

N = int(input())

n0 = n1 = n2 = 1
for n in range(1, N):
    n0, n1, n2 = (n0 + n1 + n2), (n0 + n1), (n0 + n1)
print((n0 + n1 + n2) % 9901)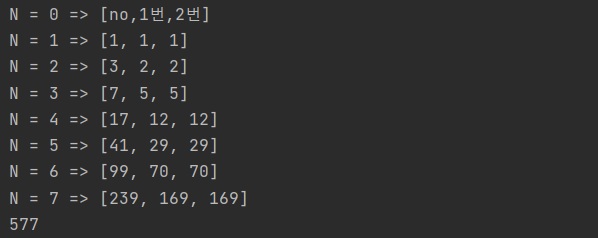

⏩ no : 사자를 배치 않할 때
⏩ 1번 : 왼쪽에 배칠 할 때
⏩ 2번 : 오른쪽에 배칠 할 때
⏩ 각 N에 대해 사자를 안 넣는, 왼쪽에 넣는, 오른쪽에 넣는 경우의 수를 dp 테이블에 나타낸다.
⏩ N = 2 번 테이블에서 사자를 안 넣을 때의 경우의 수를 구할 때 N = 1 번 테이블의 경우의 수 중 모든 케이스들이 가능하다
⏩ N = 2 번 테이블에서 사자를 1에 넣을 때의 경우의 수를 구할 때 N = 1 번 테이블의 1에 넣는 케이스를 제외하고 가능하다.
⏩ 이렇게 N-1의 테이블을 활용해서 N 테이블을 채워나갈 수 있다.

💯 경우의 수를 구하는 DP 문제의 경우 마치 Tree 구조처럼 이전 경우의 수와 다음 경우의 수에 상관관계가 있는지를 판단해서 접근하는것도 좋을 듯 하다.