BFS(너비 우선 탐색)

BFS는 탐색 시작점에서 인접한 정점들을 전부 탐색한 뒤, 다음 인접한 정점을 탐색하는 알고리즘이다. 일반적으로 최단 경로를 찾는 문제에서 많이 사용되는 알고리즘이다.

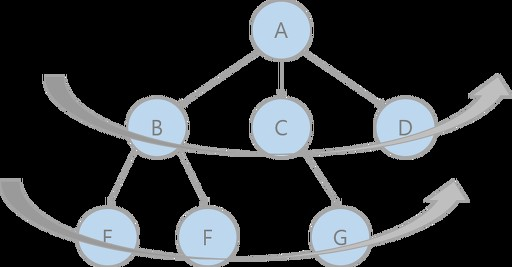
1. 1차 배열 정점

# 그래프 경로 저장
V, E = map(int,input().split())         
G = [[] for _ in range(V+1)]
edges = list(map(int,input().split()))

for i in range(0, E*2, 2):
    u,v = edges[i],edges[i+1]
    G[u].append(v)
    G[v].append(u)

# 너비 우선 탐색 시작
vi = [0] * (V+1)           # 방문지점은 정점 + 1
Q = []                     # Q 공간 생성
Q.append(1)                # 큐 시작점       
vi[1] = 1                  # 첫 방문 등록 

while Q:   
    now = Q.pop(0)                 # 먼저 방문한 지점을 pop
    for next in G[now]:            # 인접 지점 for문으로 전부 방문
        if not vi[next]:           # 방문한 곳이 아닐 경우만
            Q.append(next)         # next를 큐에 삽입, 탐색할 경로 저장
            vi[next] = vi[now] + 1 # 방문표시 및 거리표시

# 인접경로 전부를 for문으로 Q에 enQ하고
# 탐색 경로 V에 저장 하는 값이 Q.pop(0) 즉 Q에 맨 왼쪽값이자
# 먼저 들어온 정점을 V에 저장하고 탐색한다.

2. 2차 배열 정점

from collections import deque

def BFS(r,c):
    Q = deque()
    Q.append((r,c))
    G[r][c] = 0
    while Q:
        r,c = Q.popleft()
        for dr,dc in ((-1,0),(0,1),(1,0),(0,-1)):
            nr, nc = r + dr, c + dc
            if 0 <= nr < N and 0 <= nc < M and G[nr][nc] == 1:
                Q.append((nr,nc))
                G[nr][nc] = 0

N, M, K = map(int,input().split())
G = [[0] * M for _ in range(N)]     # 빈 그래프 생성

for _ in range(K):
    r,c = map(int,input().split())  
    G[r][c] = 1           		    # 그래프에 경로 표시

for r in range(N):
    for c in range(M):
        if G[r][c] == 1:
            BFS(r,c)

• G그래프를 생성한다.
• vi 배열이 필요하면 vi도 만들지만, G를 사용할 수 있으면 사용하자
• 시작점 좌표를 가지고 BFS함수로 들어가자