백준 1987_알파벳

https://www.acmicpc.net/problem/1987

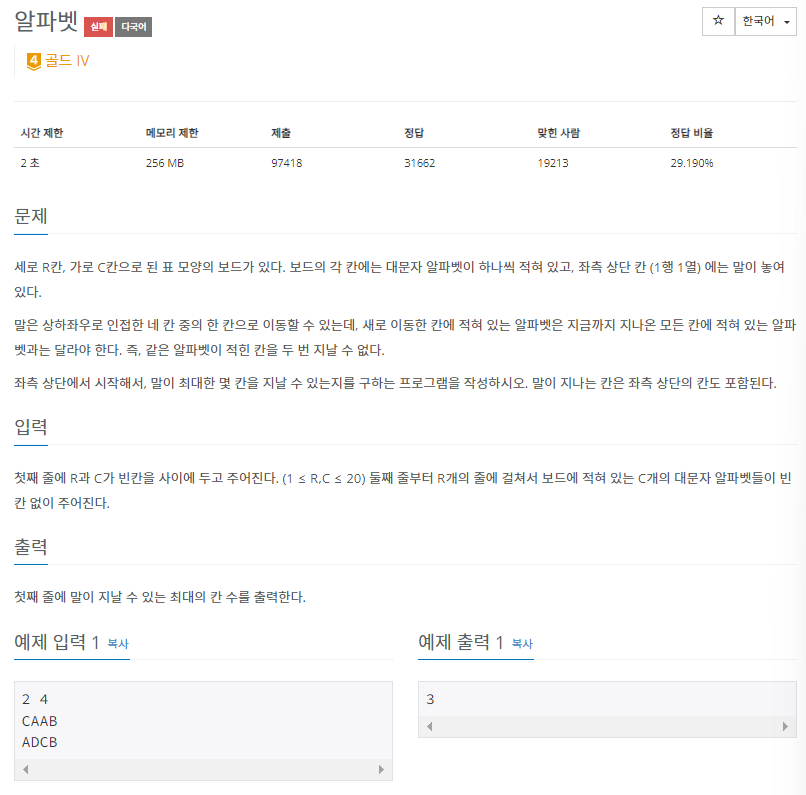
해당 문제는 (0,0) 지점에서 조건에 부합하게 이동할 수 있는 최장거리를 구하는 문제다. 가장 먼 거리를 구해야했기 때문에 DFS를 먼저 떠올렸다. 그러나 일반적인 DFS를 했을 때, 첫 경로가 갔던 길을 두 번째 경로가 지나치지 못하기 때문에 모든 경우를 탐색할 수 없었다.

1. 일반적인 DFS (틀림)

R, C = map(int,input().split())
G1 = [list(input()) for _ in range(R)]
G2 = [[0] * C for _ in range(R)]

S = [[0,0]]
vi = [G1[0][0]]
route = 1
G2[0][0] = route

while S:
   for dr, dc in ((0,1),(1,0),(0,-1),(-1,0)):
       nr, nc = S[-1][0] + dr, S[-1][1] + dc
       if 0 <= nr < R and 0 <= nc < C:
           if G1[nr][nc] not in vi and G2[nr][nc] <= G2[S[-1][0]][S[-1][1]]:
               S.append((nr,nc))
               vi.append(G1[nr][nc])
               route += 1
               G2[nr][nc] = route
               break
   else:
       S.pop()
       vi.pop()
       route -= 1

print(max([max(lst) for lst in G2]))

결국에는 첫 번쨰 경로가 탐색했던 경로와 겹치더라도 두 번째 경로가 지나갈 수 있도록 코드를 짜야했다.

2. DFS + 백트래킹

R, C = map(int,input().split())
G = [list(input()) for _ in range(R)]
ch = [0] * 26

def DFS(r,c,cnt):
    global Max
    Max = max(cnt,Max)

    for dr, dc in ((1,0),(0,1),(-1,0),(0,-1)):
        nr, nc = r + dr, c + dc
        if 0 <= nr < R and 0 <= nc <C and ch[ord(G[nr][nc])-65] == 0:
            ch[ord(G[nr][nc]) - 65] = 1
            DFS(nr,nc,cnt+1)
            ch[ord(G[nr][nc]) - 65] = 0

Max = 1
ch[ord(G[0][0])-65] = 1
DFS(0,0,Max)

print(Max)

신기하다. DFS 갈수 있는 지점 중 임의로 하나를 선택해 이동을 하다가 갈 곳이 없게 되면 갈 수 있는 경로가 있는 지점으로 돌아가 탐색을 하는 알고리즘이다. 이 때 방문했던 곳을 재방문하는것을 방지하기 위해서 VI 방문배열을 사용한다. 하지만!!! 여기서는 방문지점을 표시할 수가 없다. 왜냐하면, 모든 탐색의 경우의 수를 탐색해야하기 때문이다. 방문지점을 표기하면 지나간 곳은 영원히 지날 수 없게된다. 그래서 백트래킹을 사용해서 방문 지점을 표시해주는 것이 아니라 문제에 경로 조건을 만족하도록 ch[ord(G[nr][nc]) - 65] = 1 조건을 달아주고 ch[ord(G[nr][nc]) - 65] = 0 표시를 없애며 다시 원위치 할 수 있는 코드를 구성헀다.

💯 다양한 알고리즘을 배웠는데, 이렇게 두가지 개념을 합쳐볼 생각은 해보지 못한 것 같다. 또한, DFS의 형식에 너무 얽매였던 것 같다. 외워둔 형식에서 벗어나 유연한 사고를 해야할 것 같다.