Dijkstra
다익스트라 알고리즘은 DP를 활용한 대표적인 최단 경로 탐색 알고리즘이다. 특정한 하나의 정점에서 다른 모든 정점으로 가는 최단 경로를 알려준다.
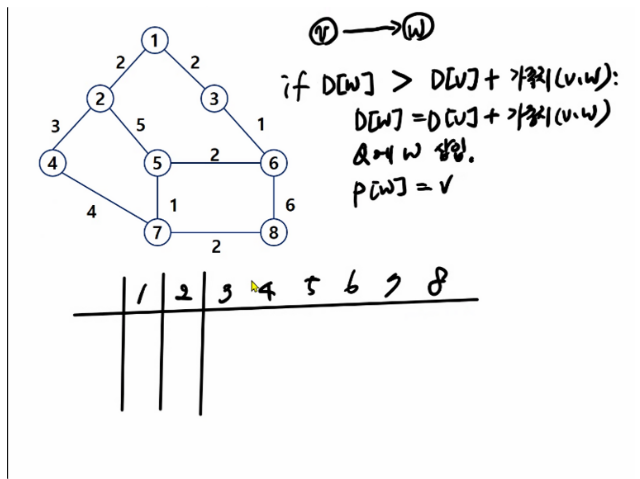
1. deque를 이용한 Dijkstra
from collections import deque
# 교수님 풀이
Test = int(input())
for TC in range(Test):
N, E = map(int,input().split())
G = [[] for _ in range(N+1)]
for _ in range(E):
u, v, weight = map(int,input().split())
G[u].append((v,weight))
Q = deque()
Q.append(0)
D = [0xfffff] * (N + 1)
D[0] = 0
# BFS 풀이 방법
while Q:
u = Q.popleft()
for v, weight in G[u]:
if D[v] > D[u] + weight:
D[v] = D[u] + weight
Q.append(v)
print(f'#{TC+1}', D[N])⏩ D = [0xfffff] * (N + 1) 가중치의 합을 저장하는 D 리스트에 굉장히 큰 값을 초기에 넣어준다.
⏩ D[v] > D[u] + weight 가중치의 합 비교를 통해 작은 값이 업데이트 되도록 한다.
⏩ 시작정점을 기준으로 BFS처럼 노드를 탐색하며, 가중치의 최소값을 갱신한다.
💯 So, 방문했던 노드를 또 방문하며 최소 가중치를 업데이트 하기 때문에 속도가 느리다.
2. heap을 이용한 Dijkstra
(1) heap
우선순위가 높은 데이터를 가장 먼저 삭제하는 자료구조이다.
⭐ 최소 힙
from heapq import heappop, heappush
h = []
heappush(h,value)
heappop(h) ⭐ 최대 힙
from heapq import heappop, heappush
h = []
heappush(h,-value)
-heappop(h) ⭐ 기존리스트를 힙으로 변환
from heapq import heapify
heap = [4, 1, 7, 3, 8, 5]
heapify(heap)
print(heap)
#=====================
[1, 3, 5, 4, 8, 7] (2) Dijkstra
from heapq import heappop, heappush
INF = int(1e9)
Test = int(input())
for TC in range(Test):
N, E = map(int,input().split())
G = [[] for _ in range(N+1)]
for _ in range(E):
u, v, weight = map(int,input().split())
G[u].append((v,weight))
h = []
heappush(h,(0,start))
Distance = [INF] * (N + 1)
Distance[start] = 0
while h:
start_distance, start = heappop(h)
if Distance[start] < start_distance : continue
for next, weigth in G[start]:
if Distance[next] > Distance[start] + weigth:
Distance[next] = Distance[start] + weigth
heappush(h,(Distance[start] + weigth,next))
⏩ 최단 경로인 경우 위치와(next), 그 위치로의 최단 경로가(Distance[start] + weigth) h에 heap에 의해서 저장됨
⏩ 이 위치(next)를 가지고 다음 이동을 해야하는데, 현재 위치(next)의 거리와 저장되어 있던 ((Distance[start] + weigth) 이 값을 비교
⏩ 현재 위치(next)의 거리가 더 작으면은 이동할 필요가 없다.why?? 이미 최단 거리니깐
⏩ 한 번 처리된 노드의 최단 거리는 고정
⏩ 종료 시 테이블에 각 노드까지의 최단 거리 정보가 저장

