이진트리

모든 노드들이 2개의 서브트리를 가지는 특별한 현태의 트리이다.

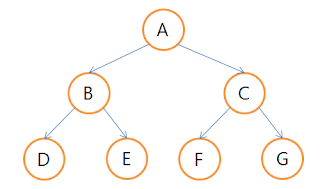
1. 이진트리 종류

(1) 포화 이진 트리(Full Binary Tree)

모든 레벨의 노드가 포화상태로 차 있는 이진 트리이다.

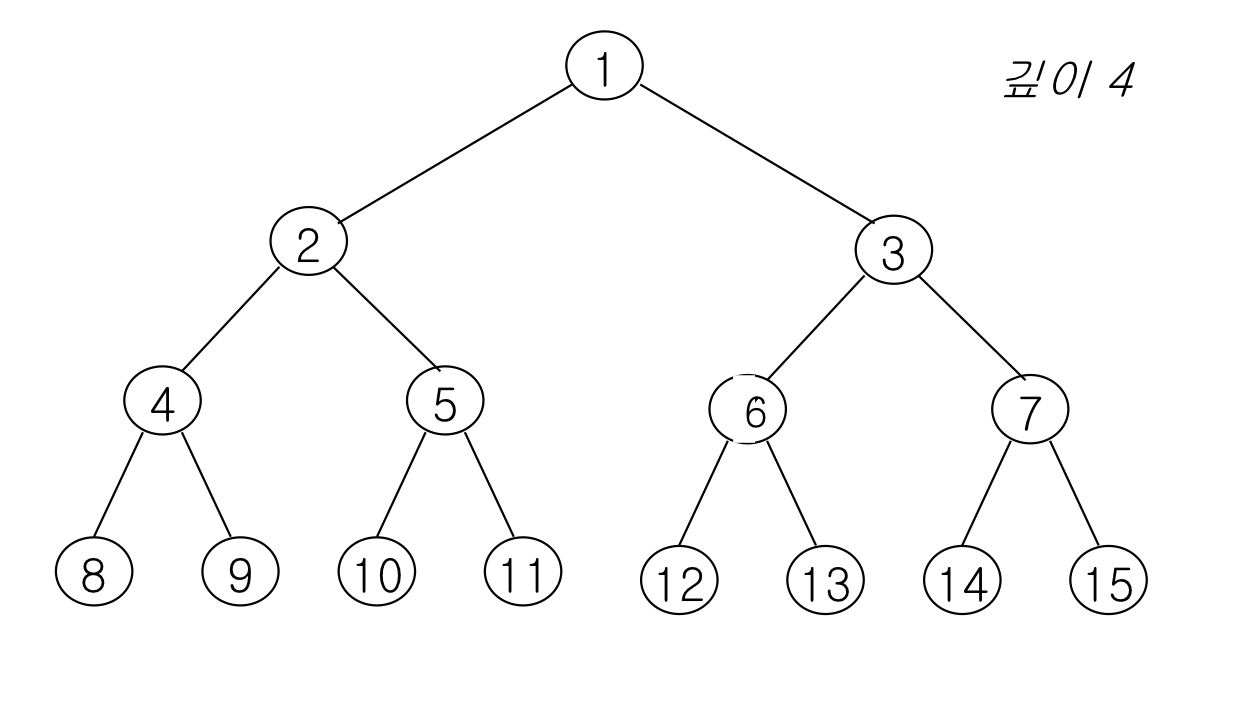
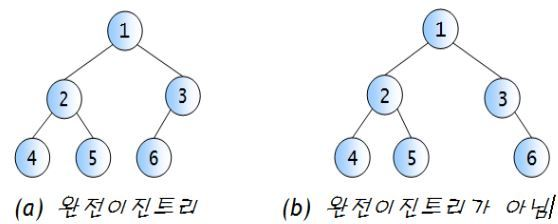
(2) 완전 이진 트리(Complete Binary Tree)

위에서 아래로, 왼쪽에서 오른쪽으로 노드가 채워 지는데, 이 때 중간에 빠진 노드가 하나도 없이 순차적으로 쌓여있는 이진 트리이다. 인덱스를 연속적으로 부여할 수 있는 장점을 가진다.

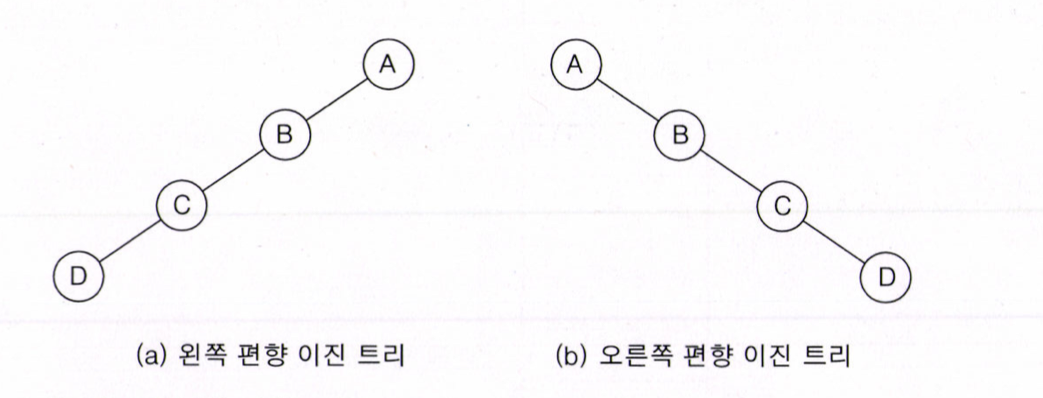
(3) 편향 이진 트리(Skewed Binary Tree)

한쪽 방향으로만 자식 노드를 가지는 이진 트리이다.
왼쪽으로만 가지면 "왼쪽 편향 이진트리", 오른쪽으로만 가지면 "오른쪽 편향 이진트리" 라고한다.

2. 이진트리 - 순회(traversal)

(1) 전위순회(preorder traveral : VLR)

• 부모노드 방문 → 자식노드 좌,우

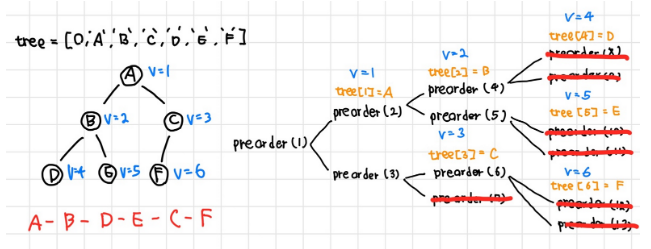
#트리
tree = [0, 'A','B','C','D','E','F']
last_node = 6

# 전위 순회
def preorder(v):
    if v > last_node:
        return
    
    print(tree[v], end=' ')
    preorder(v*2)# 왼쪽
    preorder(v*2+1)# 오른쪽

(2) 중위순회(inorder traveral : LVR)

• 왼쪽 자식노드 → 부모노드 → 오른쪽 자식노드

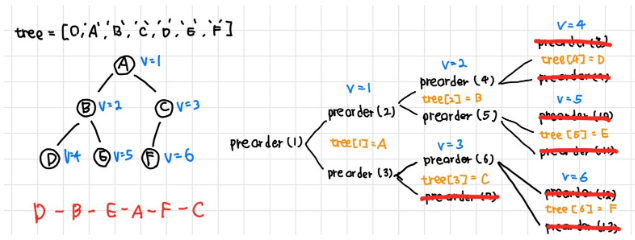
tree = [0, 'A','B','C','D','E','F']
last_node = 6

# 중위 순회
def inorder(v):
    if v > last_node:
        return
    
    inorder(v*2) # 왼쪽
    print(tree[v],end=' ')
    inorder(v*2+1) # 오른쪽

(3) 후위순회(postorder traveral : LRV)

• 자식노드 좌, 우 → 부모노드

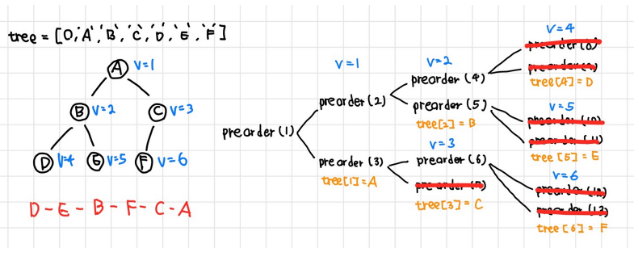
tree = [0, 'A','B','C','D','E','F']
last_node = 6

def postorder(v):
    if v > last_node:
        return
    
    postorder(v*2) # 왼쪽
    postorder(v*2+1) # 오른쪽
    print(tree[v], end=' ')

3. SubTree

자식 노드에 대한 부모노드를 P 리스트에 저장한다.

def subtree(v):
    if v == 0:return
    global cnt
    cnt += 1
    subtree(L[v])
    subtree(R[v])

V,E = map(int,input().split())

L = [0] * (V+1)
R = [0] * (V+1)
P = [0] * (V+1)

arr = list(map(int,input().split()))
for i in range(0,E*2,2):
    p, c = arr[i], arr[i+1]
    if L[p] == 0:
        L[p] = c
    else:
        R[p] = c

inorder(1)
subtree(3) ; print('cnt' , cnt)