1. 신장 트리(Spanning tree)
신장트리란 그래프에서 모든 정점을 포함하고 정점 간 서로 연결이 되며 싸이클이 존재하지 않는 tree 그래프를 의미한다.
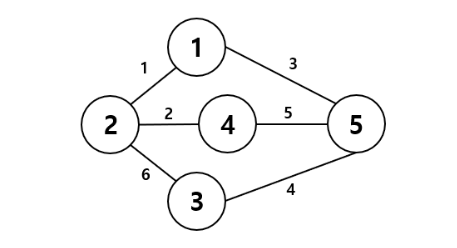
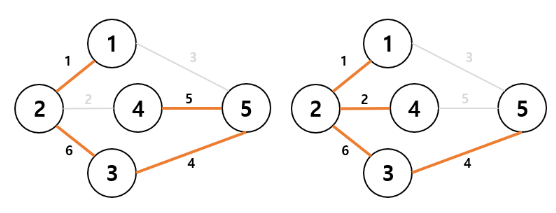
- 위의 그래프에서 아래와 같은 그래프가 나올 수 있다.
- 아래 그래프와 같은 그래프들을 신장트리라 칭한다.
2. 최소 신장 트리(Minimum Spanning Tree, MST)
신장트리는 각각의 간선들이 가중치를 가지고있다. 신하나의 그래프에서 생성되는 신장트리들 중, 가중치의 합이 최소가 되는 신장트리를 최소 신장 트리라한다.
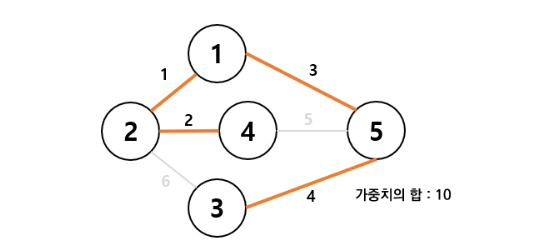
- 위와 같은 그래프가 최소신장트리이다.
3. 크루스칼(Kruskal)
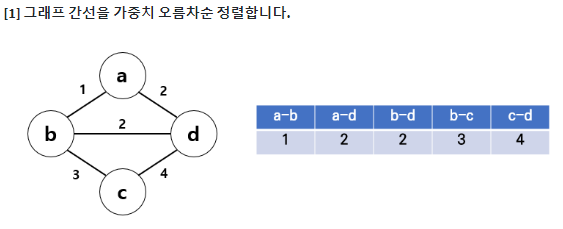
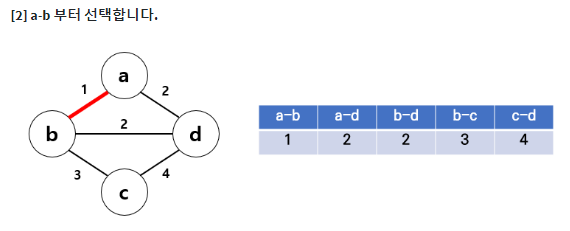
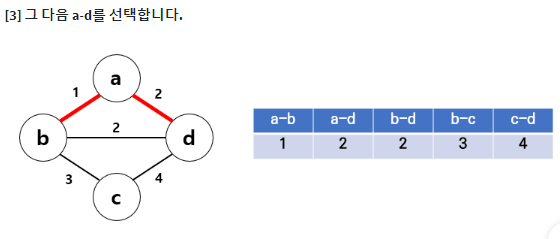
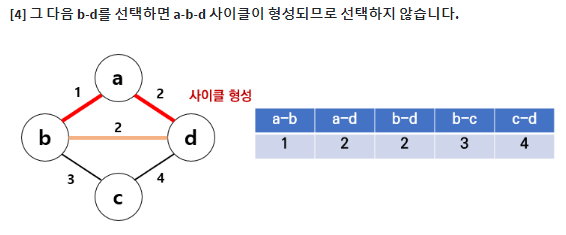
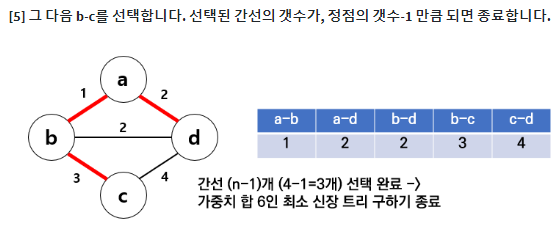
크루스칼 알고리즘은 그리디 알고리즘의 일종이다. 최소 신장 트리를 구하는데 사용하는 대표적인 알고리즘이다. 가중치를 기준으로 오름차순 정렬한 뒤, 사이클을 형성하지 않는 선에서 간선을 선택한다.
⭐ example
def find_parent(sp):
if sp != parent[sp]:
parent[sp] = find_parent(parent[sp])
return parent[sp]
def union(sp, ep):
parent[find_parent(sp)] = find_parent(ep)
V, E = map(int,input().split())
parent = [i for i in range(V + 1)]
G = []
for _ in range(E):
u,v,w = map(int,input().split())
G.append([u,v,w])
# 가중치 기준 오름차순 정렬
G.sort(key=lambda x:x[2])
# N개 정점(V+1), N-1개의 간선 선택
N = V + 1
Min = 0 # MST에 포함된 간선의 가중치 합
edge = 0 # 간선 수 카운팅
MST = []
for sp, ep, weight in G:
if find_parent(sp) != find_parent(ep): # 각각의 대표가 다르다 = 사이클이 생기지 않는다.
MST.append([sp,ep,w])
Min += weight
edge += 1
union(sp,ep)
if edge == N-1:
break
