Hash Table
hash table, hash map, hash 표는 키(key)를 값(value)에 매핑할 수 있는 자료구조이다. 순서에 맞춰 저장되어야 하는 데이터가 있을 경우 사용하는 array와 달리 빠르게 검색해야 할 일이 있을 때 사용한다.
예를 들어, "데이터 중 1이란 값을 갖는 데이터가 있는가?"를 빠르게 판단해야 할 경우에 대해 가정한다. 이때, 이 데이터들을 array에 저장하게 된다면 array 내에서 1이란 데이터를 찾기 위해서는 O(n)의 시간까지 소요될 수 있다. 하지만 이를 hash table, hash map 등의 자료구조에 저장하게 1이란 숫자를 key로 저장해두고 추후 O(1)의 시간을 들여 hash table의 key 중 1이 존재하는지 확인한다. 따라서 검색에 최적화된 자료구조이다.
hash table은 해시 함수를 통해 해싱한 값을 저장소의 index로 사용한다.
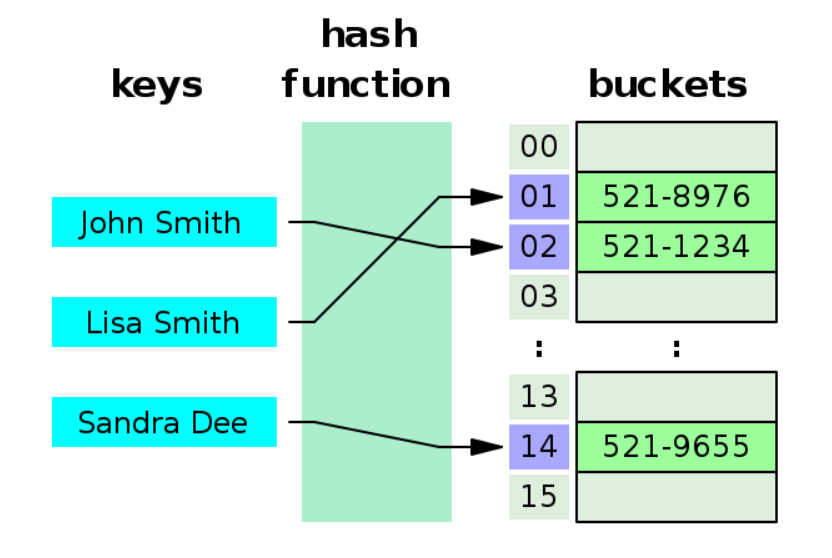
hash table의 key-value 쌍 중에서 key 값은 고유한 값이다. 따라서 John Smith에 대한 value가 저장되는 곳과 Lisa Smith에 대한 value가 저장되는 곳은 서로 다른 곳을 지정하고 있어야만 한다.
Q. key 값이 고유하다면 key값을 index로 지정하지 뭐하러 해시 함수를 통해 해싱한 값을 저장소의 index로 사용하는가?
▶ key 값을 그대로 사용하게 될 경우 key의 길이만큼의 저장 공간을 따로 해야 함과 동시에 이 저장 공간이 각 key마다 제각각일 수 있다. 따라서 해시 함수를 통해 고정된 길이값을 갖는 해싱 값을 index로 사용한다.
이때, 서로 다른 key가 주어졌을 때 해시 함수의 output으로 동일한 결과를 얻게 되는 경우가 존재한다. 이를 해시 충돌(hash collision)이라고 한다.
Hash Collision, 해시충돌
해시 충돌을 해결하기 위한 방법으로는 대표적으로 2가지가 존재한다.
- Chaining(Close Addressing)
해시 충돌이 발생하면 키에 해당하는 데이터들을 연결하는 방식이다.
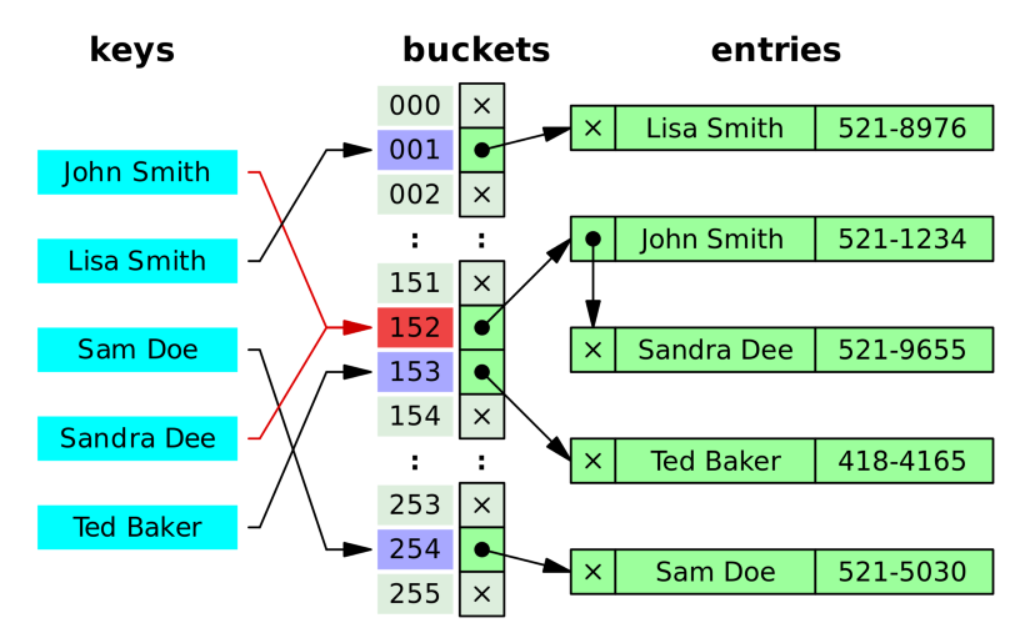
위의 그림에서 John Smith를 해싱한 값과 Sandra Dee를 해싱한 값이 152로 동일하게 나타나고 있다. John Smith가 먼저 저장되어 152의 저장공간에 들어가 있었다고 가정할 때, 추가로 저장해준 Sandra Dee의 정보를 John Smith의 정보 뒤에 linked list로 연결해주는 방식이 바로 chaining 방식이다.
충돌을 대비하여 공간을 많이 할당해 둘 필요 없이 충돌이 발생할 때마다 공간을 만들어 연결만 해주면 된다는 장점이 존재한다. 하지만 같은 hash값에 많은 데이터들이 들어가게 되면 O(1)이었던 검색 효율이 낮아지게 된다.(연결 리스트 내에서 해당 값을 찾아내야 함)
- Open Addressing
해시 충돌이 발생하면 비어 있는 hash에 데이터를 저장하는 방식이다. hash 값과 value값이 1:1인 관계를 유지한다.
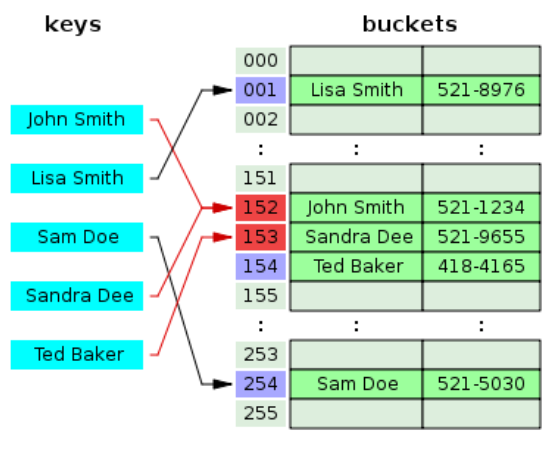
1번에서와 마찬가지로 John Smith와 Sandra Dee의 해싱 값이 152로 일치하는 상황이다. 이때, 1번이 Sandra Dee를 152의 저장공간 뒤에 연결하는 chainnig 방법과 달리 Open Addressing에서는 152 다음의 비어있는 153의 공간에 Sandra Dee의 정보를 저장한다. 위의 그림에서는 Ted Baker의 해싱 값이 153이어서 해당 저장 공간에 저장하려 했으나 이미 1:1로 대응된 value 값이 존재하여 비어있는 공간인 154의 저장 공간에 저장되고 있는 것도 알 수 있다. 이처럼 같은 해싱 값이 존재할 때 비어 있는 다른 hash값의 저장 공간을 찾아 저장하는 방법이 open addressing이다. 위의 그림에서는 1의 고정폭으로 건너 뛰며 비어있는 해시가 나오면 저장하는 선형 탐색을 하고 있다.
선형 탐색 외에도 1칸 -> 4칸 -> 9칸 -> ...칸씩 건너뛰며 빈칸을 찾는 제곱 탐색, 해시 충돌 시 다른 해시 함수를 한번 더 적용해 그 해싱값에 저장하는 방법인 이중 해시도 open addressing에 속한다.
chaining 방법과 달리 포인터(연결리스트 때문에 필요한 것)가 필요없고, 추가적 공간도 필요하지 않다. 기존의 공간에서 계속 빈 공간을 찾아 넣는 방식이기 때문이다. 하지만 특정 위치에만 데이터가 몰리게 될 수 있고, 비어있는 버킷을 찾지 못하고 원래의 해시 값으로 되돌아 올 수 있다는 단점이 존재한다.
고른 해싱값을 갖는 해시 함수
위에서 언급한 두 방식으로 해시 충돌을 해결할 수 있으나, 해시 충돌은 웬만하면 일어나지 않도록 막는 것이 가장 좋은 방법이다. 따라서 특정 값에 치우치지 않고 해싱 값을 고르게 만들어 내는 좋은 해싱 함수를 사용하는 것이 중요하다. 이러한 해싱 함수를 개선하기 위한 방법에 대해 살펴본다.
-
division method
가장 기본적인 해시 함수로, key 값을 해시 테이블의 크기로 나눈 나머지를 해시 값으로 변환한다. 간단하여 빠른 연산이 가능하다. 해시의 중복을 방지하고자 해시 테이블의 크기는 소수인 것이 좋다.
남는 공간이 발생해 메모리상으로 비효율적일 수 있다. -
multiplication method
숫자인 key값을 k, 0<A<1의 실수 A가 있을 때 h(k) = (ka mod 1)m으로 계산하는 함수이다. 2진수 연산에 최적화된 컴퓨터 구조를 고려한 해시함수이다. -
universal hashing
여러개의 해시 함수를 만들고, 이 해시 함수들의 집합 H에서 무작위로 해시 함수를 선택해 해싱하는 방법이다. 서로 다른 해시 함수는 서로 다른 해싱값을 만들어내므로 특정 값에 치우칠 확률을 줄이고 있다.
Open Addressing에서의 데이터 삭제
Java의 Hash Map에서는 Separate Chaining 방식으로 해시 충돌을 해결하고 있다. open addressing은 데이터를 삭제할 때 효율적으로 동작하기 어렵기 때문이다.
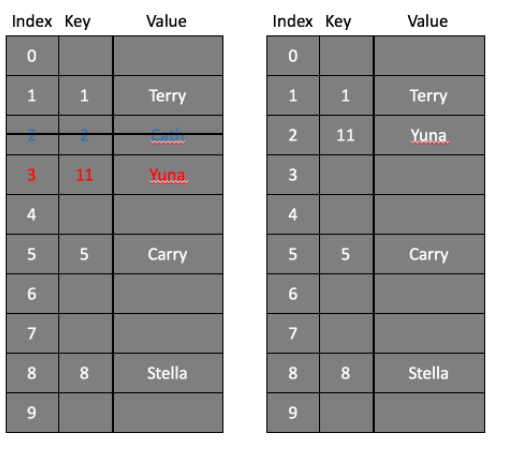
위의 그림은 key값을 10으로 나눈 나머지 값을 index 값으로 리턴하는 해시함수를 사용하고 있다. index 1에 Terry가 들어가고, index 2에 Cath가 들어간 상황에서 Yuna가 1의 해싱값을 갖게 되어 해시 충돌이 발생한다. index 1에서 해시 충돌이 발생하였으므로 2에 저장하려 했더니 2도 이미 Cath 데이터가 저장되어 있다. 따라서 Yuna 데이터는 3에 저장된다.
이때, index 2의 Cath 데이터를 삭제한다. 이 경우 11번의 key에 대해 검색하면 index 1을 먼저 찾고 그 다음 칸은 index 2를 찾게 된다. 하지만 2에는 아무런 데이터가 존재하지 않고 있어 검색은 종료된다. 따라서 key값이 11인 데이터가 저장되어 있음에도 불구하고 찾을 수 없는 문제가 발생한다. 이러한 문제를 방지하기 위해 index 2의 데이터를 삭제한 후 Dummy node를 삽입해 둔다고 한다. 다음 index로의 검색을 연결해주는 역할을 담당하는 것이다.
[참조] https://javannspring.tistory.com/238
[참조] https://go-coding.tistory.com/30
[참조] https://bcho.tistory.com/1072
