• https://mygumi.tistory.com/361
• 진수 변환
• https://rebro.kr/63
• https://stackoverflow.com/questions/16926130/convert-to-binary-and-keep-leading-zeros
• https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=jh20s&logNo=221150706030

---

비트마스크

집합의 요소들의 구성 여부를 표현할 때 유용한 방법이다.

• 작은 메모리와 빠른 수행시간으로 해결할 수 있다.
• 집합을 배열의 인덱스로 표현할 수 있다.

비트 연산

AND, OR, XOR, NOT, SHIFT

• AND (&) 둘다 참일때만 참

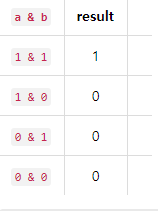
• OR (|) 둘 중 하나만 참이여도 참

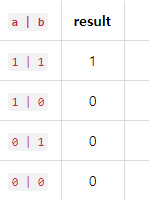
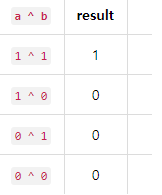
• XOR (^) 둘 중 하나만 참일 때 참

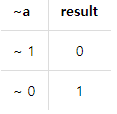
• NOT(~) 보수 연산

• SHIFT(<<) 변수의 값을 왼쪽으로 지정된 비트 수 만큼 이동

  • a << 2 = 240 → 1111 0000
  • 0001 → 0010 → 0100 → 1000 : 1 → 2 → 4 → 8
  • n * 2^b
    • (a + b) * 2 를 (a + b) << 1 로 표현할 수 있다.

• SHIFT(>>) 변수의 값을 오른쪽으로 지정된 비트 수 만큼 이동

  • a >> 2 = 15 → 0000 1111
  • 1000 → 0100 → 0010 → 0001 : 8 → 4 → 2 → 1
  • n / 2^b
    • (a + b) / 2 를 (a + b) >> 1 로 표현할 수 있다.

비트마스크를 이용한 집합연산

# 공집합
>>> A = 0
>>> bin(A)
'0b0'

# 꽉 찬 집합	
>>> A = (1<<10)-1
>>> bin(A)
'0b1111111111'

# 원소(5) 추가	
>>> A = 1<<10
>>> bin(A)
'0b10000000000'
>>> A = A | (1<<5)
>>> bin(A)
'0b10000100000'

# 원소(5) 삭제	
>>> A = A & ~(1<<5)
>>> bin(A)
'0b10000000000'

# 원소 포함 여부	
>>> A = A | (1<<5)
>>> bin(A)
'0b10000100000'
>>> A & (1<<5) != 0
True
>>> A & (1<<4) != 0
False

# 원소 Toggle	
>>> A = (1<<10)-1
>>> bin(A)
'0b1111111111'
>>> A = A ^ (1<<5)
>>> bin(A)
'0b1111011111'

# 최소 원소 찾기	
>>> A = int("0b1100100",2)
>>> bin(A)
'0b1100100'
>>>bin(A & (-A))
'0b100'

# 최소 원소 지우기	
>>>bin(A)
'0b1100100'
>>>A = A & (A - 1)
>>>bin(A)
'0b1100000'

비트 제로패딩

>>> format(14, '#010b')
'0b00001110'
>>> format(14, '08b')
'00001110'

>>> '{:08b}'.format(1)
'00000001'
>>> '{0:08b}'.format(1)
'00000001' 

>>> var = 23
>>> f"{var:#010b}"
'0b00010111'

>>> x = 5
>>> n = 8
>>> print(f"{x:0{n}b}")
00000101

>> print(f"{1:04b}")
0001
>> print(f"{1:#04b}")
0b01

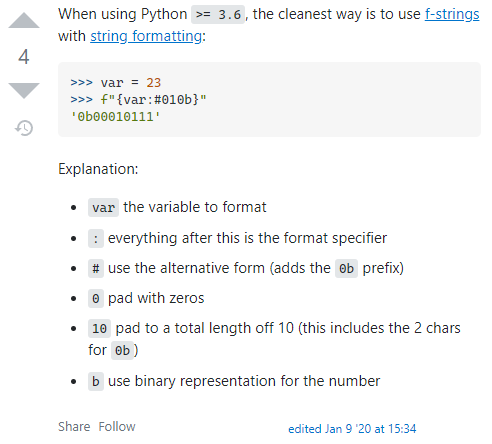
활용

부분집합

[1, 2, 3, 4, 5] 라는 집합이 있다.
해당 집합에서 임의의 부분집합을 구하는 경우 비트마스크를 활용하면 효율적이다.

# 부분집합   → 비트마스크로 표현
[1,2,3,4,5] → 11111
[2,3,4,5]   → 11110
[1,2,5]     → 10011
[2]         → 00010

경우의 수

배열 arr = [0, 1, 2, 3] 이 있을 때,
1 ~ len(arr)개의 원소를 선택하는 경우를 구해보자

itertools 의 combinations 사용
👉 시간복잡도를 고려하면 이 방법이 비트마스킹 방식보다 빠르다.

from itertools import combinations

arr = [0, 1, 2, 3]
for i in range(1, len(arr)+1):
    for case in combinations(arr, i):
        print(case)
"""
[0]
[1]
[2]
[3]
[0, 1]
[0, 2]
[0, 3]
[1, 2]
[1, 3]
[2, 3]
[0, 1, 2]
[0, 1, 3]
[0, 2, 3]
[1, 2, 3]
[0, 1, 2, 3]
"""

비트마스킹을 활용하는 경우

arr = [0, 1, 2, 3]
for i in range(1, 1 << len(arr)):
    case = []
    for k in range(len(arr)):
        if i & (1 << k):
            case.append(k)
    print(case)

"""
[0]
[1]
[0, 1]
[2]
[0, 2]
[1, 2]
[0, 1, 2]
[3]
[0, 3]
[1, 3]
[0, 1, 3]
[2, 3]
[0, 2, 3]
[1, 2, 3]
[0, 1, 2, 3]
"""

1 << len(arr)의 의미

1을 len(arr) 만큼 left shift하면 10000(2) -> 16 이다.
range(1, 16) -> 1 ~ 15
즉 0001(2) ~ 1111(2) 의 경우를 체크할 수 있다.

# 0001(2) ~ 1111(2)
0001, 0010, 0100, 1000,
0011, 0101, 1001, 0110, 1010, 1100
0111, 1011, 1101, 1110,
1111

# arr
[0], [1], [2], [3]
[0, 1], [0, 2], [0, 3], [1, 2], [1, 3], [2, 3]
[0, 1, 2], [0, 1, 3], [0, 2, 3], [1, 2, 3]
[0, 1, 2, 3]

arr 배열의 부분집합을 의미한다.
-> 즉, 1 << len(arr) 을 통해 arr 배열의 모든 부분집합을 고려할 수 있다.

if i & (1 << k):의 의미

k는 0 ~ len(arr) 의 숫자이고
i는 arr 배열의 부분집합을 의미하는 숫자이다.

i & (1 << k)으로
i라는 부분집합에 k라는 원소가 존재하는지 확인할 수 있다.

i = 10 # 1010(2)

print(i & (1 << 0) > 0) # False
print(i & (1 << 1) > 0) # True : 1 포함
print(i & (1 << 2) > 0) # False
print(i & (1 << 3) > 0) # True : 3 포함

1010(2) -> arr의 부분집합 [3, 1] 을 의미한다.
-> 즉, i & (1 << k) 을 통해 특정한 부분집합을 솎아내어 case 변수에 담을 수 있다.

교집합, 합집합, 차집합

참고

add = (a|b); # a와 b의 합집합
intersection = (a&b); # a와 b의 교집합
removed = (a&~b); # a에서 b를 뺀 차집합
toggled = (a^b); # aUb - a∩b