병합정렬 (합병정렬, Merge sort)

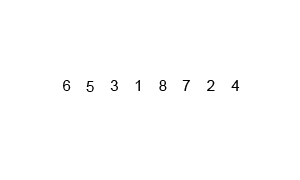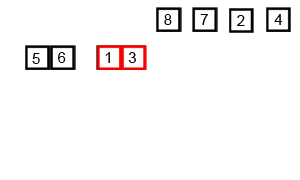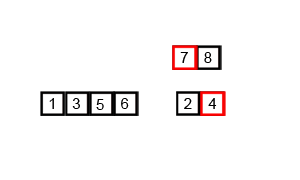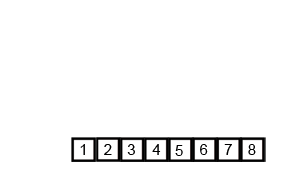
설명

분할 정복 방식으로 배열을 작은 단위로 쪼개어
쪼개진 배열들을 정렬된 상태로 병합해가면서 정렬하는 방식이다.
좋은 성능을 가진다.
빠른 정렬로 분류되고, 퀵소트와 많이 언급된다.
(분할 정복 방식을 사용한다는 측면에서 퀵소트와 유사하다)
퀵소트와 반대로 안정정렬에 속한다.

시간 복잡도

평균 : O(nlogn)
최선 : O(nlogn)
최악 : O(nlogn)

구현

def merge_sort(arr, left, right):
    if left >= right:
        return

    mid = (left + right) // 2
    merge_sort(arr, left, mid)
    merge_sort(arr, mid + 1, right)
    merge(arr, left, mid, right)

merge_sort()
퀵소트와 차이점

퀵소트 : 피벗을 통해 정렬(partition) -> 피벗 기준으로 영역을 쪼갬(quick_sort)
합병정렬 : 영역을 쪼갤 수 있을 만큼 쪼갬(merge_sort) -> 정렬(merge)

def merge(arr, left, mid, right):
    L = arr[left: mid+1]
    R = arr[mid+1: right+1]

    i = 0
    j = 0
    k = left
    lsize = len(L)
    rsize = len(R)

    print(f"-- merge {left=} {right=} {mid=} --")
    print(arr)
    print(f"{L=}")
    print(f"{R=}")

    while i < lsize and j < rsize:
        # 두 배열을 순차적으로 비교 (이미 두 배열 모두 정렬된 상태)
        if L[i] <= R[j]:
            arr[k] = L[i]
            i += 1
        else:
            arr[k] = R[j]
            j += 1
        k += 1

    # 나머지
    while i < lsize:
        arr[k] = L[i]
        k += 1
        i += 1
    while j < rsize:
        arr[k] = R[j]
        k += 1
        j += 1

    print(arr)


merge_sort(arr, 0, len(arr)-1)
print(arr, "!!")
"""
-- merge left=0 right=1 mid=0 --
[1, 4, 0, 6, 8, 3, 2, 5, 7, 3, 5, 8, 7, 7, 9, 3]
L=[1]
R=[4]
[1, 4, 0, 6, 8, 3, 2, 5, 7, 3, 5, 8, 7, 7, 9, 3]
-- merge left=2 right=3 mid=2 --
[1, 4, 0, 6, 8, 3, 2, 5, 7, 3, 5, 8, 7, 7, 9, 3]
L=[0]
R=[6]
[1, 4, 0, 6, 8, 3, 2, 5, 7, 3, 5, 8, 7, 7, 9, 3]
-- merge left=0 right=3 mid=1 --
[1, 4, 0, 6, 8, 3, 2, 5, 7, 3, 5, 8, 7, 7, 9, 3]
L=[1, 4]
R=[0, 6]
[0, 1, 4, 6, 8, 3, 2, 5, 7, 3, 5, 8, 7, 7, 9, 3]
-- merge left=4 right=5 mid=4 --
[0, 1, 4, 6, 8, 3, 2, 5, 7, 3, 5, 8, 7, 7, 9, 3]
L=[8]
R=[3]
[0, 1, 4, 6, 3, 8, 2, 5, 7, 3, 5, 8, 7, 7, 9, 3]
-- merge left=6 right=7 mid=6 --
[0, 1, 4, 6, 3, 8, 2, 5, 7, 3, 5, 8, 7, 7, 9, 3]
L=[2]
R=[5]
[0, 1, 4, 6, 3, 8, 2, 5, 7, 3, 5, 8, 7, 7, 9, 3]
-- merge left=4 right=7 mid=5 --
[0, 1, 4, 6, 3, 8, 2, 5, 7, 3, 5, 8, 7, 7, 9, 3]
L=[3, 8]
R=[2, 5]
[0, 1, 4, 6, 2, 3, 5, 8, 7, 3, 5, 8, 7, 7, 9, 3]
-- merge left=0 right=7 mid=3 --
[0, 1, 4, 6, 2, 3, 5, 8, 7, 3, 5, 8, 7, 7, 9, 3]
L=[0, 1, 4, 6]
R=[2, 3, 5, 8]
[0, 1, 2, 3, 4, 5, 6, 8, 7, 3, 5, 8, 7, 7, 9, 3]
-- merge left=8 right=9 mid=8 --
[0, 1, 2, 3, 4, 5, 6, 8, 7, 3, 5, 8, 7, 7, 9, 3]
L=[7]
R=[3]
[0, 1, 2, 3, 4, 5, 6, 8, 3, 7, 5, 8, 7, 7, 9, 3]
-- merge left=10 right=11 mid=10 --
[0, 1, 2, 3, 4, 5, 6, 8, 3, 7, 5, 8, 7, 7, 9, 3]
L=[5]
R=[8]
[0, 1, 2, 3, 4, 5, 6, 8, 3, 7, 5, 8, 7, 7, 9, 3]
-- merge left=8 right=11 mid=9 --
[0, 1, 2, 3, 4, 5, 6, 8, 3, 7, 5, 8, 7, 7, 9, 3]
L=[3, 7]
R=[5, 8]
[0, 1, 2, 3, 4, 5, 6, 8, 3, 5, 7, 8, 7, 7, 9, 3]
-- merge left=12 right=13 mid=12 --
[0, 1, 2, 3, 4, 5, 6, 8, 3, 5, 7, 8, 7, 7, 9, 3]
L=[7]
R=[7]
[0, 1, 2, 3, 4, 5, 6, 8, 3, 5, 7, 8, 7, 7, 9, 3]
-- merge left=14 right=15 mid=14 --
[0, 1, 2, 3, 4, 5, 6, 8, 3, 5, 7, 8, 7, 7, 9, 3]
L=[9]
R=[3]
[0, 1, 2, 3, 4, 5, 6, 8, 3, 5, 7, 8, 7, 7, 3, 9]
-- merge left=12 right=15 mid=13 --
[0, 1, 2, 3, 4, 5, 6, 8, 3, 5, 7, 8, 7, 7, 3, 9]
L=[7, 7]
R=[3, 9]
[0, 1, 2, 3, 4, 5, 6, 8, 3, 5, 7, 8, 3, 7, 7, 9]
-- merge left=8 right=15 mid=11 --
[0, 1, 2, 3, 4, 5, 6, 8, 3, 5, 7, 8, 3, 7, 7, 9]
L=[3, 5, 7, 8]
R=[3, 7, 7, 9]
[0, 1, 2, 3, 4, 5, 6, 8, 3, 3, 5, 7, 7, 7, 8, 9]
-- merge left=0 right=15 mid=7 --
[0, 1, 2, 3, 4, 5, 6, 8, 3, 3, 5, 7, 7, 7, 8, 9]
L=[0, 1, 2, 3, 4, 5, 6, 8]
R=[3, 3, 5, 7, 7, 7, 8, 9]
[0, 1, 2, 3, 3, 3, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9]
[0, 1, 2, 3, 3, 3, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9] !!
"""

합병 대상의 두 영역이 각각 정렬되어있으므로
단순하게 두 배열을 순차적으로 비교하면서 정렬할 수 있다.

합병정렬은 순차적인 비교를 하기 때문에
LinkedList 정렬에 합병정렬을 사용하면 효율적이다.

만약 LinkedList 를 퀵정렬을 통해 정렬하게 되면 성능이 좋지 못하다.

• 퀵 정렬은 합병정렬과 다르게 순차적으로 비교하는게 아닌 임의접근으로 비교하기 때문이다.
• 그리고 LinkedList는 삽입,삭제 연산에서는 유용하지만 접근 연산에서는 비효율적이기 때문이다. (배열은 [i]처럼 인덱스로 O(1) 수준의 접근이 가능하지만, LinkedList는 HEAD부터 탐색해야 하므로 O(N) 이다)

=> LinkedList를 퀵정렬을 사용하여 정렬하면 오버헤드가 증가한다.

---

힙 정렬 (heap sort)

설명

최대 힙 트리 혹은 최소 힙 트리를 구성하여 정렬하는 방법이다.
완전 이진 트리를 기본으로 하는 Heap 자료구조를 이용한 정렬 방식이다.

불안정 정렬에 속한다.

시간복잡도

평균 : O(nlogn)
최선 : O(nlogn)
최악 : O(nlogn)

과정

1. 최대 힙을 구성한다.
2. 힙의 루트 노드에는 가장 큰 값이 존재한다.
   루트 노드의 값을 pop하고
   루트 노드에 마지막 요소를 넣은 뒤, 힙의 크기를 하나 줄인다.
3. 힙의 크기가 1보다 크면 1,2번 과정을 반복한다.

루트 노드의 값을 계속 pop하면 내림차순 정렬의 효과를 가진다.

구현

def heap_sort(arr):
    n = len(arr)

    # 최대 힙 초기화
    for i in range(n // 2 - 1, -1, -1):
        # 일반 배열을 힙으로 구성한다.
        heapify(arr, n, i)
        
    print("최대 힙 초기화")
    print(arr)
    print()

    # extract 연산
    for i in range(n - 1, 0, -1):
        arr[0], arr[i] = arr[i], arr[0]
        # 요소가 하나 제거된 이후에 다시 최대 힙을 구성하는 과정이다
        # n-1부터 1번 인덱스까지만 heapify한다. (0번 인덱스 = 루트 노드)
        heapify(arr, i, 0)

i : n//2 -1 ~ 0까지 인덱스가 도는 이유
i가 부모노드 일때,
왼쪽 자식 노드는 2i + 1, 오른쪽 자식 노드는 2i + 2이다.

def heapify(arr, n, i):
    parent = i  # 부모노드
    left = i * 2 + 1  # 왼쪽 자식 노드의 위치
    right = i * 2 + 2  # 오른쪽 자식 노드의 위치
    
    print(arr)
    print(f"parent={parent}({arr[parent]})")
    print(f"{left=} {right=}")
    # 왼쪽 자식 노드
    if left < n and arr[parent] < arr[left]:
        parent = left

    # 오른쪽 자식 노드
    if right < n and arr[parent] < arr[right]:
        parent = right
        
    # 부모 노드 < 왼쪽 혹은 오른쪽 자식 노드
    if i != parent:
        print(f"부모 < 자식 {parent}({arr[parent]})")
        # 최대 힙을 구성할 때까지 부모노드와 자식노드를 swap하며
        # 재귀적으로 진행
        arr[parent], arr[i] = arr[i], arr[parent]
        print(arr,"!!")
        heapify(arr, n, parent)
    else:
        print("부모 >= 자식")


heap_sort(arr)
print("heap sort result\n", arr)
"""
최대 힙 초기화
[9, 8, 8, 7, 5, 7, 7, 5, 6, 3, 4, 3, 1, 0, 2, 3]

[3, 8, 8, 7, 5, 7, 7, 5, 6, 3, 4, 3, 1, 0, 2, 9]
parent=0(3)
left=1 right=2
부모 < 자식 1(8)
[8, 3, 8, 7, 5, 7, 7, 5, 6, 3, 4, 3, 1, 0, 2, 9] !!
[8, 3, 8, 7, 5, 7, 7, 5, 6, 3, 4, 3, 1, 0, 2, 9]
parent=1(3)
left=3 right=4
부모 < 자식 3(7)
[8, 7, 8, 3, 5, 7, 7, 5, 6, 3, 4, 3, 1, 0, 2, 9] !!
[8, 7, 8, 3, 5, 7, 7, 5, 6, 3, 4, 3, 1, 0, 2, 9]
parent=3(3)
left=7 right=8
부모 < 자식 8(6)
[8, 7, 8, 6, 5, 7, 7, 5, 3, 3, 4, 3, 1, 0, 2, 9] !!
[8, 7, 8, 6, 5, 7, 7, 5, 3, 3, 4, 3, 1, 0, 2, 9]
parent=8(3)
left=17 right=18
부모 >= 자식
[2, 7, 8, 6, 5, 7, 7, 5, 3, 3, 4, 3, 1, 0, 8, 9]
parent=0(2)
left=1 right=2
부모 < 자식 2(8)
[8, 7, 2, 6, 5, 7, 7, 5, 3, 3, 4, 3, 1, 0, 8, 9] !!
[8, 7, 2, 6, 5, 7, 7, 5, 3, 3, 4, 3, 1, 0, 8, 9]
parent=2(2)
left=5 right=6
부모 < 자식 5(7)
[8, 7, 7, 6, 5, 2, 7, 5, 3, 3, 4, 3, 1, 0, 8, 9] !!
[8, 7, 7, 6, 5, 2, 7, 5, 3, 3, 4, 3, 1, 0, 8, 9]
parent=5(2)
left=11 right=12
부모 < 자식 11(3)
[8, 7, 7, 6, 5, 3, 7, 5, 3, 3, 4, 2, 1, 0, 8, 9] !!
[8, 7, 7, 6, 5, 3, 7, 5, 3, 3, 4, 2, 1, 0, 8, 9]
parent=11(2)
left=23 right=24
부모 >= 자식
[0, 7, 7, 6, 5, 3, 7, 5, 3, 3, 4, 2, 1, 8, 8, 9]
parent=0(0)
left=1 right=2
부모 < 자식 1(7)
[7, 0, 7, 6, 5, 3, 7, 5, 3, 3, 4, 2, 1, 8, 8, 9] !!
[7, 0, 7, 6, 5, 3, 7, 5, 3, 3, 4, 2, 1, 8, 8, 9]
parent=1(0)
left=3 right=4
부모 < 자식 3(6)
[7, 6, 7, 0, 5, 3, 7, 5, 3, 3, 4, 2, 1, 8, 8, 9] !!
[7, 6, 7, 0, 5, 3, 7, 5, 3, 3, 4, 2, 1, 8, 8, 9]
parent=3(0)
left=7 right=8
부모 < 자식 7(5)
[7, 6, 7, 5, 5, 3, 7, 0, 3, 3, 4, 2, 1, 8, 8, 9] !!
[7, 6, 7, 5, 5, 3, 7, 0, 3, 3, 4, 2, 1, 8, 8, 9]
parent=7(0)
left=15 right=16
부모 >= 자식
[1, 6, 7, 5, 5, 3, 7, 0, 3, 3, 4, 2, 7, 8, 8, 9]
parent=0(1)
left=1 right=2
부모 < 자식 2(7)
[7, 6, 1, 5, 5, 3, 7, 0, 3, 3, 4, 2, 7, 8, 8, 9] !!
[7, 6, 1, 5, 5, 3, 7, 0, 3, 3, 4, 2, 7, 8, 8, 9]
parent=2(1)
left=5 right=6
부모 < 자식 6(7)
[7, 6, 7, 5, 5, 3, 1, 0, 3, 3, 4, 2, 7, 8, 8, 9] !!
[7, 6, 7, 5, 5, 3, 1, 0, 3, 3, 4, 2, 7, 8, 8, 9]
parent=6(1)
left=13 right=14
부모 >= 자식
[2, 6, 7, 5, 5, 3, 1, 0, 3, 3, 4, 7, 7, 8, 8, 9]
parent=0(2)
left=1 right=2
부모 < 자식 2(7)
[7, 6, 2, 5, 5, 3, 1, 0, 3, 3, 4, 7, 7, 8, 8, 9] !!
[7, 6, 2, 5, 5, 3, 1, 0, 3, 3, 4, 7, 7, 8, 8, 9]
parent=2(2)
left=5 right=6
부모 < 자식 5(3)
[7, 6, 3, 5, 5, 2, 1, 0, 3, 3, 4, 7, 7, 8, 8, 9] !!
[7, 6, 3, 5, 5, 2, 1, 0, 3, 3, 4, 7, 7, 8, 8, 9]
parent=5(2)
left=11 right=12
부모 >= 자식
[4, 6, 3, 5, 5, 2, 1, 0, 3, 3, 7, 7, 7, 8, 8, 9]
parent=0(4)
left=1 right=2
부모 < 자식 1(6)
[6, 4, 3, 5, 5, 2, 1, 0, 3, 3, 7, 7, 7, 8, 8, 9] !!
[6, 4, 3, 5, 5, 2, 1, 0, 3, 3, 7, 7, 7, 8, 8, 9]
parent=1(4)
left=3 right=4
부모 < 자식 3(5)
[6, 5, 3, 4, 5, 2, 1, 0, 3, 3, 7, 7, 7, 8, 8, 9] !!
[6, 5, 3, 4, 5, 2, 1, 0, 3, 3, 7, 7, 7, 8, 8, 9]
parent=3(4)
left=7 right=8
부모 >= 자식
[3, 5, 3, 4, 5, 2, 1, 0, 3, 6, 7, 7, 7, 8, 8, 9]
parent=0(3)
left=1 right=2
부모 < 자식 1(5)
[5, 3, 3, 4, 5, 2, 1, 0, 3, 6, 7, 7, 7, 8, 8, 9] !!
[5, 3, 3, 4, 5, 2, 1, 0, 3, 6, 7, 7, 7, 8, 8, 9]
parent=1(3)
left=3 right=4
부모 < 자식 4(5)
[5, 5, 3, 4, 3, 2, 1, 0, 3, 6, 7, 7, 7, 8, 8, 9] !!
[5, 5, 3, 4, 3, 2, 1, 0, 3, 6, 7, 7, 7, 8, 8, 9]
parent=4(3)
left=9 right=10
부모 >= 자식
[3, 5, 3, 4, 3, 2, 1, 0, 5, 6, 7, 7, 7, 8, 8, 9]
parent=0(3)
left=1 right=2
부모 < 자식 1(5)
[5, 3, 3, 4, 3, 2, 1, 0, 5, 6, 7, 7, 7, 8, 8, 9] !!
[5, 3, 3, 4, 3, 2, 1, 0, 5, 6, 7, 7, 7, 8, 8, 9]
parent=1(3)
left=3 right=4
부모 < 자식 3(4)
[5, 4, 3, 3, 3, 2, 1, 0, 5, 6, 7, 7, 7, 8, 8, 9] !!
[5, 4, 3, 3, 3, 2, 1, 0, 5, 6, 7, 7, 7, 8, 8, 9]
parent=3(3)
left=7 right=8
부모 >= 자식
[0, 4, 3, 3, 3, 2, 1, 5, 5, 6, 7, 7, 7, 8, 8, 9]
parent=0(0)
left=1 right=2
부모 < 자식 1(4)
[4, 0, 3, 3, 3, 2, 1, 5, 5, 6, 7, 7, 7, 8, 8, 9] !!
[4, 0, 3, 3, 3, 2, 1, 5, 5, 6, 7, 7, 7, 8, 8, 9]
parent=1(0)
left=3 right=4
부모 < 자식 3(3)
[4, 3, 3, 0, 3, 2, 1, 5, 5, 6, 7, 7, 7, 8, 8, 9] !!
[4, 3, 3, 0, 3, 2, 1, 5, 5, 6, 7, 7, 7, 8, 8, 9]
parent=3(0)
left=7 right=8
부모 >= 자식
[1, 3, 3, 0, 3, 2, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9]
parent=0(1)
left=1 right=2
부모 < 자식 1(3)
[3, 1, 3, 0, 3, 2, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9] !!
[3, 1, 3, 0, 3, 2, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9]
parent=1(1)
left=3 right=4
부모 < 자식 4(3)
[3, 3, 3, 0, 1, 2, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9] !!
[3, 3, 3, 0, 1, 2, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9]
parent=4(1)
left=9 right=10
부모 >= 자식
[2, 3, 3, 0, 1, 3, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9]
parent=0(2)
left=1 right=2
부모 < 자식 1(3)
[3, 2, 3, 0, 1, 3, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9] !!
[3, 2, 3, 0, 1, 3, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9]
parent=1(2)
left=3 right=4
부모 >= 자식
[1, 2, 3, 0, 3, 3, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9]
parent=0(1)
left=1 right=2
부모 < 자식 2(3)
[3, 2, 1, 0, 3, 3, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9] !!
[3, 2, 1, 0, 3, 3, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9]
parent=2(1)
left=5 right=6
부모 >= 자식
[0, 2, 1, 3, 3, 3, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9]
parent=0(0)
left=1 right=2
부모 < 자식 1(2)
[2, 0, 1, 3, 3, 3, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9] !!
[2, 0, 1, 3, 3, 3, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9]
parent=1(0)
left=3 right=4
부모 >= 자식
[1, 0, 2, 3, 3, 3, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9]
parent=0(1)
left=1 right=2
부모 >= 자식
[0, 1, 2, 3, 3, 3, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9]
parent=0(0)
left=1 right=2
부모 >= 자식
heap sort result
 [0, 1, 2, 3, 3, 3, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9]
"""

최대 힙을 구성할 때까지
부모노드와 자식노드를 교환하며 재귀적으로 진행한다.

퀵정렬, 합병정렬의 성능이 좋기 때문에
힙 정렬의 사용빈도가 높지 않다.

힙정렬이 유용한 경우

가장 크거나 가장 작은 값을 구하는 경우
-> 최대 힙의 경우 가장 큰값이 루트 노드에 있으므로 O(1)
-> 최소 힙의 경우 가장 작은 값이 루트 노드에 있으므로 O(1)

최대 k만큼 떨어진 요소를 정렬할 때
삽입 정렬보다 개선된 결과를 얻을 수 있다.

---

계수 정렬 (Counting sort)

• https://www.youtube.com/watch?v=1g_K4wIMcEA

설명

n개의 원소의 배열을 모두 정렬하는 가짓수는 N!이다.
comparison sort를 통해 생기는 트리 말단 노드가 N!이상의 갯수를 가지기 위해서 2^h >=N!를 만족하는 트리의 높이 h를 가져야하고 h > O(nlogn)이다.

이런 O(nlgn)을 줄일 수 있는 방법은 Comparison을 하지 않는 것

시간복잡도

O(n+k)
k: 배열에서 등장하는 최댓값

공간복잡도

O(k)
k 만큼의 배열을 만들어야 한다.

counting 과정이 필요하다. (비교과정이 없다. 단순히 세기만 하면 된다)

구현

def counting_sort(arr):
    n = len(arr)
    max_num = max(max(arr), n)
    sorted_arr = [0 for _ in range(max_num + 1)]

    # counting 배열에 arr의 최댓값이 담기도록 범위를 max_num+1로 설정
    counting = [0 for _ in range(max_num + 1)]

    # counting 배열의 값을 증가시킨다.
    for i in range(n):
        counting[arr[i]] += 1
    print(f"{counting=}")

    # counting 배열을 누적합
    for i in range(1, n):
        counting[i] += counting[i-1]
    print(f"{counting=}")

    for i in reversed(range(n)):
        sorted_arr[counting[arr[i]]] = arr[i]
        counting[arr[i]] -= 1 # 남은 갯수를 -1
        print(f"{sorted_arr}")

print(arr)
counting_sort(arr)
"""
[1, 4, 0, 6, 8, 3, 2, 5, 7, 3, 5, 8, 7, 7, 9, 3]
counting=[1, 1, 1, 3, 1, 2, 1, 3, 2, 1, 0, 0, 0, 0, 0, 0, 0]
counting=[1, 2, 3, 6, 7, 9, 10, 13, 15, 16, 16, 16, 16, 16, 16, 16, 0]   
[0, 0, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 9]
[0, 0, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 7, 0, 0, 9]
[0, 0, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 7, 7, 0, 0, 9]
[0, 0, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 7, 7, 0, 8, 9]
[0, 0, 0, 0, 0, 0, 3, 0, 0, 5, 0, 0, 7, 7, 0, 8, 9]
[0, 0, 0, 0, 0, 3, 3, 0, 0, 5, 0, 0, 7, 7, 0, 8, 9]
[0, 0, 0, 0, 0, 3, 3, 0, 0, 5, 0, 7, 7, 7, 0, 8, 9]
[0, 0, 0, 0, 0, 3, 3, 0, 5, 5, 0, 7, 7, 7, 0, 8, 9]
[0, 0, 0, 2, 0, 3, 3, 0, 5, 5, 0, 7, 7, 7, 0, 8, 9]
[0, 0, 0, 2, 3, 3, 3, 0, 5, 5, 0, 7, 7, 7, 0, 8, 9]
[0, 0, 0, 2, 3, 3, 3, 0, 5, 5, 0, 7, 7, 7, 8, 8, 9]
[0, 0, 0, 2, 3, 3, 3, 0, 5, 5, 6, 7, 7, 7, 8, 8, 9]
[0, 0, 0, 2, 3, 3, 3, 0, 5, 5, 6, 7, 7, 7, 8, 8, 9]
[0, 0, 0, 2, 3, 3, 3, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9]
[0, 0, 1, 2, 3, 3, 3, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9]
"""

기수 정렬 (Radix sort)

• https://www.youtube.com/watch?v=j9SGZIbIhxM

설명

데이터를 구성하는 기본 요소를 이용하여 정렬하는 방식이다.

10진수에서 1, 10, 100 .. 처럼 증가하는 가중치를 기수라고 한다. (수를 이루는 기초적인 가중치 수 = 기수)
숫자 423에서 백의 자리 수 4은 눈으로 보기에4이지만
기초가 되는 수가 100이므로 400이다

기수 정렬은 계수 정렬을 숫자의 자릿 수 마다 실행하는 방법이다.
즉, 각 숫자의 자리 수들로만 이루어진 배열을 추출한뒤,
이를 계수 정렬을 하는 것이다.

시간복잡도

O(d * (n + b))
d : 정렬할 숫자의 자릴 수
b : 10 (k와 같으나 10으로 고정됨)

counting sort의 경우 O(n + k)로 배열의 최댓값 k에 영향을 받는다

장점

문자열, 정수 정렬이 가능하다

단점

자릿수가 없는 것은 정렬할 수 없다 (부동소숫점)
중간 결과를 저장할 bucket이란 공간이 필요하다.

구현

def radix_sort(arr):
    print(arr)
    n = len(arr)
    m = len(str(max(arr)))

    counting = [[0 for _ in range(n)] for _ in range(m)]
    for i in range(m):
        temp = [0 for _ in range(n)]
        
        for j in range(n):
            idx = int(f"{arr[j]:0{m}}"[m-1-i])
            counting[i][idx] += 1
            
        for j in range(n-1):
            counting[i][j+1] += counting[i][j]
        print(counting[i])
        
        for j in reversed(range(n)):
            idx = int(f"{arr[j]:0{m}}"[m-1-i])
            counting[i][idx] -= 1
            temp[counting[i][idx]] = arr[j]
            
        arr = temp
        print(i, arr)
    print(arr)


arr = [8, 26, 23, 11, 27, 501, 2, 34, 56, 253]
radix_sort(arr)
"""
[8, 26, 23, 11, 27, 501, 2, 34, 56, 253]
[0, 2, 3, 5, 6, 6, 8, 9, 10, 10]
0 [11, 501, 2, 23, 253, 34, 26, 56, 27, 8]
[3, 4, 7, 8, 8, 10, 10, 10, 10, 10]
1 [501, 2, 8, 11, 23, 26, 27, 34, 253, 56]
[8, 8, 9, 9, 9, 10, 10, 10, 10, 10]
2 [2, 8, 11, 23, 26, 27, 34, 56, 253, 501]
[2, 8, 11, 23, 26, 27, 34, 56, 253, 501]
"""

MSD -> 가장 큰 자리수부터 counting sort
LSD -> 가장 낮은 자리수부터 counting sort

LSD는 16000, 1을 비교할 때 digit 개수만큼 따져야하지만
MSD는 마지막 수까지 확인할 필요가 없다

LSD는 중간에 정렬 결과를 알 수 없다
MSD는 중간에 정렬 결과를 알 수 있다. 정렬이 되었는지 확인하는 과정이 필요하고 이 때문에 메모리를 더 사용한다.

LSD는 알고리즘이 일관되어 있다. => 따라서 기수 정렬은 주로 LSD를 언급한다.