이진 탐색 & 매개 변수 탐색

hyyyynjn·2021년 7월 7일

lower bound upper bound 매개 변수 탐색 이진 탐색

알고리즘 정리

목록 보기

1/12

이진 탐색

정렬된 배열에서만 사용할 수 있다

배열 내부의 데이터가 정렬되어 있어야 사용 가능한 알고리즘이다.
탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 특징이 있다.
- 변수 3개 = 시작점, 끝잠, 중간점
- 찾으려는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교하여 원하는 데이터를 찾는다.

이진 탐색 동작 과정

1.단계

0	2	4	6	8	10	12	14	16	18
시작점[0]				중간점[4]					끝점[9]

시작점과 끝점을 확인한 후 중간점을 정한다.
- 중간점이 실수라면 소수점 이하를 버린다.
중간점[4]의 데이터와 찾으려는 데이터 4를 비교한다.
- 중간점의 데이터가 더 크므로(8) 확인할 필요없이 끝점을 [4] 이전의 [3]으로 옮긴다.

2.단계

0	2	4	6	8	10	12	14	16	18
시작점[0]	중간점[1]		끝점[3]

시작점[0]과 끝점[3]의 중간점[1]을 구한다.
- 중간점에 위치한 데이터 2 는 찾으려는 데이터 4보다 작으므로 중간점 이하의 데이터는 확인할 필요가 없다
- 시작점을 [2]로 변경한다.

3.단계

0	2	4	6	8	10	12	14	16	18
		시작점[2],중간점[2]	끝점[3]

시작점[2]과 끝점[3]의 중간점[2]을 구한다.
중간점에 위치한 데이터와 찾으려는 데이터가 동일하므로 현 시점에서 탐색을 종료한다.

전체 데이터는 10개이지만 이진 탐색을 이용하면 총 3번의 탐색으로 원소를 찾을 수 있다.

한번 확인할 때마다 확인하는 원소의 개수가 절반씩 줄어든다.

시간 복잡도 : O(logN)

재귀함수로 구현한 이진 탐색

def binary_search(array, target, start, end):
  if start > end:
    return None

  mid = (start + end) // 2

  if array[mid] == target:
    return mid
  elif array[mid] > target:
    return binary_search(array, target, start, mid - 1)
  elif array[mid] < target:
    return binary_search(array, target, mid + 1, end)


n, target = map(int, input().split())
array = list(map(int, input().split()))

result = binary_search(array, target, 0, n - 1)
if result is None:
  print("원소가 존재하지 않습니다.")
else:
  print(result + 1)

반복문으로 구현한 이진 탐색

def binary_search(array, target, start, end):
  while start <= end:
    mid = (start + end) // 2

    if array[mid] == target:
      return mid
    elif array[mid] > target:
      end = mid - 1
    else:
      start = mid + 1
  return None


n, target = map(int, input().split())
array = list(map(int, input().split()))

result = binary_search(array, target, 0, n - 1)
if result is None:
  print("원소가 존재하지 않습니다.")
else:
  print(result + 1)

Lower Bound & Upper Bound

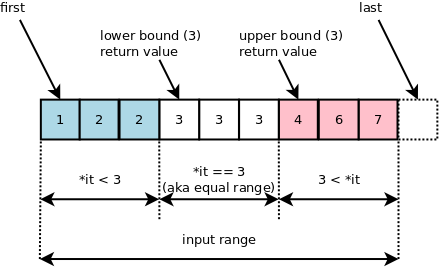
Lower bound는 데이터 내에서 특정 값보다 같거나 큰 값이 처음 나오는 위치를 리턴해준다.

파이썬 bisect 모듈의 bisect_left

lower_bound 함수

def lower_bound(data, target):
    lo = 0
    hi = len(data)
    while lo < hi:
        mid = (lo + hi) // 2
        if target <= data[mid]:
            hi = mid
        else:
            lo = mid + 1
    return lo

bisect_left 함수

def bisect_left(a, x, lo=0, hi=None):
    if lo < 0:
        raise ValueError('lo must be non-negative')
    if hi is None:
        hi = len(a)
    while lo < hi:
        mid = (lo+hi)//2
        # Use __lt__ to match the logic in list.sort() and in heapq
        if a[mid] < x: lo = mid+1
        else: hi = mid
    return lo

Upper Bound는 특정 값보다 처음으로 큰 값이나 나오는 위치를 리턴해준다.

파이썬 bisect 모듈의 bisect_right

upper_bound 함수

def upper_bound(data, target):
    lo = 0
    hi = len(data)

    while lo < hi:
        mid = (lo + hi) // 2
        if target >= data[mid]:
            lo = mid + 1
        else:
            hi = mid
    return lo
    
    
arr=[50, 80, 81, 150, 150, 150, 150, 210, 260]
target=150
lower_bound = 3
upper_bound = 7

bisect_right 함수

def bisect_right(a, x, lo=0, hi=None):
    if lo < 0:
        raise ValueError('lo must be non-negative')
    if hi is None:
        hi = len(a)
    while lo < hi:
        mid = (lo+hi)//2
        # Use __lt__ to match the logic in list.sort() and in heapq
        if x < a[mid]: hi = mid
        else: lo = mid+1
    return lo

매개 변수 탐색

최적화 문제를 결정 문제로 풀 수 있는 기술

최적화 문제 👉 어떤 알고리즘의 최적의 솔루션을 찾아내는 것
결정 문제 👉 답이 이미 결정되어있다고 보고 문제를 푸는 것 (징검다리 문제)

매개 변수 탐색 문제를 언제 사용할 수 있을까?

결정 문제로 풀 수 있는 문제
어떤 시점까지는 조건을 만족하지만, 그 시점 이후로는 조건을 만족하지 않는 경우에서 최댓값 찾기 (Upper Bound)
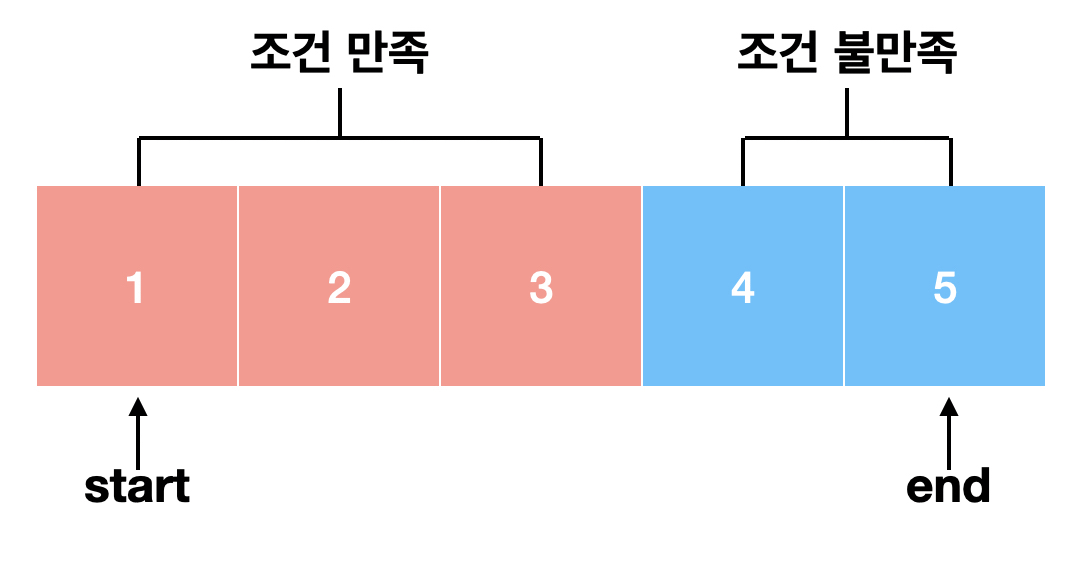
어떤 시점까지는 조건을 만족하지 않지만, 그 시점 이후로는 조건을 만족하는 경우에서 최소값 찾기 (Lower Bound)

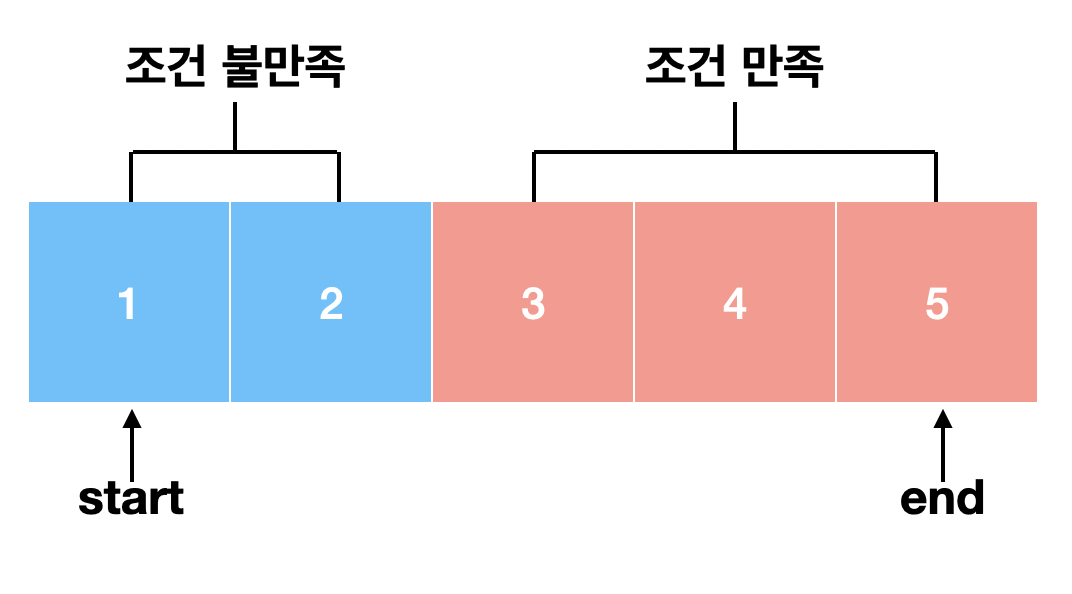
매개 변수 탐색의 동작 과정

문제에서 최종적으로 찾고자하는 최솟값/최댓값을 매개변수로 본다.
결정 함수를 정의하고 구현했을 때 결과 배열이 연속인지 확인한다.
최솟값이면 결정 함수의 결과가 [f,f,...,t,t] 에서 f->t 로 바뀌는 부분을 찾는다.
최댓값이면 결정 함수의 결과가 [t,t,...,f,f] 에서 t->f 로 바뀌는 부분을 찾는다.

이진 탐색과의 차이점

이진 탐색 👉 target과 일치한 값을 찾으면, 함수를 종료하고 위치 반환
매개 변수 탐색 👉 target과 일치하는 값을 찾아도 함수를 종료하지 않고 더이상 탐색할 배열이 남아있지 않을 때까지 탐색을 계속한다.

매개 변수 구간 정의

# 1
def binary_search(arr,lo,hi,value):
    while lo + 1 < hi:
        mid = (lo + hi) // 2
        if arr[mid] <= value:
          lo = mid
        else:
          hi = mid
    return arr[lo]

조건 lo + 1 < hi 👉 반복문 내에서 arr[lo] < arr[hi]가 항상 성립한다.
lo와 hi가 1씩 차이가 날 경우 (hi-lo == 1)
👉 mid <=hi 또는 lo <= mid 가 되어
arr[lo] < arr[hi]가 성립하지 않을 수 있지만
lo와 hi가 1이상 차이 날 경우 (hi-lo > 1)
👉 arr[lo] < arr[hi] 식은 불변식이 된다.
값을 찾는 조건에 따라 lo 또는 hi가 정답이 된다
- 조건 arr[mid] <= value 👉 arr[lo] == value 이다.
- 조건 arr[mid] < value 👉 arr[hi] == value 이다.
lo, hi 구간을 정의 👉 lo = 구간의 최솟값 -1 & hi = 구간의 최댓값
- lo = 구간의 최솟값 으로 정의할 경우, hi는 구간의 최솟값이 될 수 없다.
  (lo + 1 < hi)

결정 함수 구현

# 2
def fn(param):
    pass
    
def binary_search(arr,lo,hi,value):
    while lo + 1 < hi:
        mid = (lo + hi) // 2
        if fn(mid):
          lo = mid # 참이면 오른쪽 구간을 탐색
        else:
          hi = mid # 거짓이면 왼쪽 구간을 탐색
    return arr[lo]

fn(param) := param 이 어떤 조건을 만족하면 true를 반환하고 아니면 false를 반환하게끔 구현한다.
- param 👉 일반적으로 문제에서 최종적으로 구해야 하는 최솟값/최댓값이 찾아야 하는 매개변수이다.
  - param의 범위는 연속적이여야 한다.
    - [lo, hi] 사이의 값
  - fn(param)의 범위도 연속적이여야 한다.
    - [false, false, ..., false, true, ..., true, true] 또는 [true, true, ..., true, false, ..., false, false]
    - 중간에 false -> true 또는 true -> false 로 바뀌는 부분은 1번만 존재해야 한다.
      - 만약 여러개 있을 경우, 삼분 탐색 등의 다른 방법으로 해결해야 한다.
- 어떤 조건 👉 param 이상/이하일 때 M개의 그룹으로 나눌 수 있는가 또는 M개로 분할할 수 있는가 등을 묻는 것

hyyyynjn

이전 포스트

람다식 활용

다음 포스트

다이나믹 프로그래밍

1개의 댓글

MintCat

2023년 9월 25일

도움 많이 되었습니다! 감사합니다!!!

답글 달기