최단경로 알고리즘

hyyyynjn·2021년 7월 30일

알고리즘 정리

목록 보기

3/12

https://blog.naver.com/ndb796/221234427842

✅최단경로 알고리즘

BFS (완전탐색 알고리즘)

가중치가 없거나 모든 가중치가 동일한 그래프에서 최단경로를 구하는 경우 가장 빠르다

다익스트라 알고리즘 (Dijkstra Algorithm) ✅

음이 아닌 가중 그래프에서의 단일 쌍, 단일 출발, 단일 도착 최단 경로 문제

벨만-포드 알고리즘 (Bellman-Ford-Moore Algorithm) ✅

가중 그래프에서의 단일 쌍, 단일 출발, 단일 도착 최단 경로 문제

플로이드-워셜 알고리즘 (Floyd-Warshall Algorithm) ✅

전체 쌍 최단 경로 문제

✅다익스트라 알고리즘

그래프에서 여러개의 노드가 있을 때, 특정한 노드에서 출발하여 다른 노드로 가는 각각의 최단 경로를 구하는 알고리즘이다.

⭐음수 가중치가 없을 때 정상적으로 동작한다.

그리디 알고리즘의 한 종류.

📢원리

출발 노드 설정

최단 거리 테이블 초기화

방문하지 않은 노드 중 최단 거리가 짧은 노드 선택

선택한 노드를 거쳐 다른 노드로 가는 비용을 계산 후, 최단 거리 테이블 갱신

3,4번 과정 반복

📢구현

Heap 자료구조를 사용하여 구현한다.

파이썬에서 heapq 라이브러리를 사용한다.

📌 heapq : 튜플을 원소로 받으면, 튜플의 첫번째 원소를 기준으로 우선순위 큐를 구성한다. (첫번째 원소의 값이 낮은 데이터가 먼저 삭제된다)

파이썬은 기본적으로 최소 힙(Min Heap) 구조를 이용한다.

import heapq
import sys

input = sys.stdin.readline
INF = int(1e9)

n,m = map(int, input().split())
start = int(input())

graph = [[] for i in range(n+1)]

distance = [INF] * (n+1)

for _ in range(m):
	# a번 노드에서 b번 노드로 가는 비용이 c
    a,b,c = map(int,input().split())
    graph[a].append((b,c))

def dijkstra(start):
    q = []
    heapq.heappush(q,(0,start))
    distance[start] = 0 # 시작 노드 초기화
    
    while q:
        dist, now = heapq.heappop(q)
        if dist > distance[now]: # 최단 거리 테이블의 값보다 dist가 크면 continue
            continue
    
        for i in graph[now]:
            cost = dist + i[1]  # cost : 현재 노드 now를 거쳐 다음 노드 i[1]로 가는 거리
            if distance[i[0]] > cost:
                distance[i[0]] = cost
                heapq.heappush(q,(cost, i[0]))

dijkstra(start)

✅벨만-포드 알고리즘

⭐음수 가중치가 있는 그래프의 시작 정점에서 다른 정점까지의 최단 거리를 구할 수 있다.

음수 사이클 존재의 여부를 알 수 있다.

O(VE)

📢원리

시작 정점을 결정한다.

시작 정점에서 각각 다른 정점까지의 거리 값을 무한대로 초기화한다.
(시작 정점이 a라면, distance[b] = a->b의 거리를 뜻함)
시작 정점 -> 시작 정점은 0으로 초기화한다.

현재 정점에서 모든 인접 정점들을 탐색하며, 기존에 저장되어 있는 인접 정점까지의 거리(distance[a])보다 현재 정점을 거쳐 인접 정점에 도달하는 거리가 더 짧을 경우 짧은 거리로 갱신해준다.

3번의 과정을 n-1번 반복한다.

위 과정을 모두 마치고 난 후 거리가 갱신되는 경우가 생긴다면 그래프에 음수 사이클이 존재한다는 것이다.

음수 사이클 체크 방법

n-1번 반복이 끝난 이후, 한 번 더(n번째) 위의 과정을 돌려주었을 때 값이 바뀐다면 음수 사이클이 있는 그래프임을 알 수 있다.
음수 사이클이 존재하는 경우에는 음수 가중치를 계속해서 더해주게 되어 최단 거리를 구할 수 없는 무한 루프에 빠지게 된다.

📢구현

# 벨만-포드 알고리즘
n , m = map(int, input().split()) # n 노드의 수 / m 간선의 수

graph = []

for i in range(m):
    u, v, w = list(map(int, input().split()))
    graph.append([u, v, w])


def BellmanFord(src):
    # 1. 최단거리 테이블 초기화 ( 출발노드 0 / 나머지 INF )
    dist = [float("inf") for i in range(n + 1)]
    dist[src] = 0

    # 2. 1~ n-1개의 노드를 사용한 최단거리 구하기 루프
    for i in range(n-1):
        for u, v, w in graph: # 입력받았던 그래프 돌기 /  u->v = w (비용)
            if dist[u] != float("inf") and dist[u] + w < dist[v]: 
            # 1) dist[u]가 INF가 아니고, 
            # 2) dist[u] + w (지금 계산한 최단거리) 가 dist[v] (기존 최단거리) 보다 작으면
                dist[v] = dist[u] + w # 테이블 갱신

    # 3. 음의 사이클 확인
    cycle = 0
    for u, v, w in graph:
        if dist[u] != float("inf") and dist[u] + w < dist[v]:
            print("Graph contains negative weight cycle")
            cycle = 1
            break
    if cycle == 0:
        print('Distance from source vertex',src)
        print('Vertex \t Distance from source')
        for i in range(1, len(dist)):
            print(i,'\t',dist[i])


BellmanFord(1)

✅플로이드 워셜 알고리즘

모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구하는 알고리즘이다.

매번 방문하지 않은 노드 중에서 최단 거리를 찾을 필요가 없다.

다이나믹 프로그래밍의 한 종류 (점화식 활용 Dab = min(Dab, Dak + Dkb))

📢원리

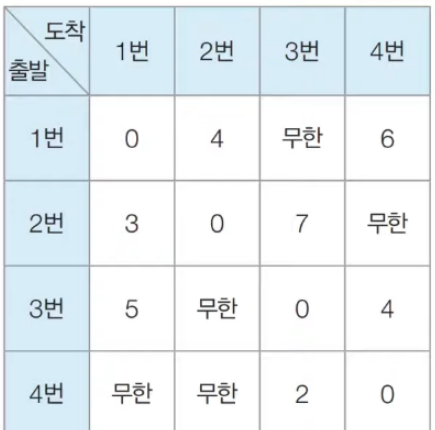
Dab : (A -> B) 로 가는 최소 비용

Dak + Dkb : (A -> K -> B) 로 가는 최소 비용

📢구현

INF = int(1e9)

# 노드 개수 & 간선 개수
n = int(input())
m = int(input())

# 2차원 리스트(그래프 표현)
graph = [[INF]*(n+1) for _ in range(n+1)]

# 자기 자신으로 가는 경로 비용 = 0
for a in range(n+1):
    for b in range(n+1):
        if a==b:
            graph[a][b]=0

# 각 간선에 대한 정보 입력
for _ in range(m):
    a,b,c = map(int,input().split())
    graph[a][b] = c

# 점화식에 따라 플로이드 워셜 알고리즘 수행
# k -> a -> b 순서
for k in range(1, n+1):
    for a in range(1,n+1):
        for b in range(1,n+1):
            # 점화식 그대로
            graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])