출처[LECTURE02]
강의 영상: https://www.youtube.com/watch?v=Nh9MIEbCJIw
해당 강의를 기반으로 추가적인 코드 구현과 설명을 정리했습니다.
Statistical Perspective
데이터의 분포(PDF)
비슷한 데이터들은 비슷한 분포를 갖고있습니다. 말로 들으면 그럴싸하다. 조금더 자세히 확인하기 위해 강아지와 자동차 사진들의 데이터 분포를 확인해보겠습니다.
ResNet-18모델을 사용해서 feature를 추출하고, feature의 차원을 시각화하기 위해서 t-SNE를 사용해 3차원으로 축소합니다.
자동차 사진




강아지 사진




import os
import cv2
import torch
import torchvision.models as models
import torchvision.transforms as transforms
import numpy as np
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
# 1. 임베딩을 추출할 ResNet18모델
model = models.resnet18(pretrained=True)
model = torch.nn.Sequential(*list(model.children())[:-1]) # Remove the last layer to get features
model.eval()
# 2. Image transformation(전처리)
data_transform = transforms.Compose([
transforms.ToPILImage(),
transforms.Resize((224, 224)),
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]),
])
# 3. 이미지 경로 설정
car_images_path = "/workspace/Generative_lhk/car"
dog_images_path = "/workspace/Generative_lhk/dog"
car_images = [os.path.join(car_images_path, img) for img in os.listdir(car_images_path) if img.endswith('.jpg')]
dog_images = [os.path.join(dog_images_path, img) for img in os.listdir(dog_images_path) if img.endswith('.jpg')]
all_images = car_images + dog_images
labels = [0] * len(car_images) + [1] * len(dog_images) # 0 for car, 1 for dog
# 4. feature 추출
def extract_features(image_paths):
features = []
with torch.no_grad():
for img_path in image_paths:
img = cv2.imread(img_path)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
img = data_transform(img).unsqueeze(0)
feature = model(img).squeeze().numpy()
features.append(feature)
return np.array(features)
features = extract_features(all_images)
# 5. t-SNE를 사용해서 2차원으로 축소(시각화 하기 위해서)
tsne = TSNE(n_components=3, random_state=42, perplexity=min(30, len(features) - 1))
features_3d = tsne.fit_transform(features)
# 6. 시각화
fig = plt.figure(figsize=(10, 6))
ax = fig.add_subplot(111, projection='3d')
for i, label in enumerate(set(labels)):
indices = [j for j, x in enumerate(labels) if x == label]
ax.scatter(features_3d[indices, 0], features_3d[indices, 1], features_3d[indices, 2], label="Car" if label == 0 else "Dog", alpha=0.6)
plt.legend()
plt.title("t-SNE 3D Visualization of Car and Dog Image Features")
ax.set_xlabel("t-SNE Component 1")
ax.set_ylabel("t-SNE Component 2")
ax.set_zlabel("t-SNE Component 3")
plt.show()
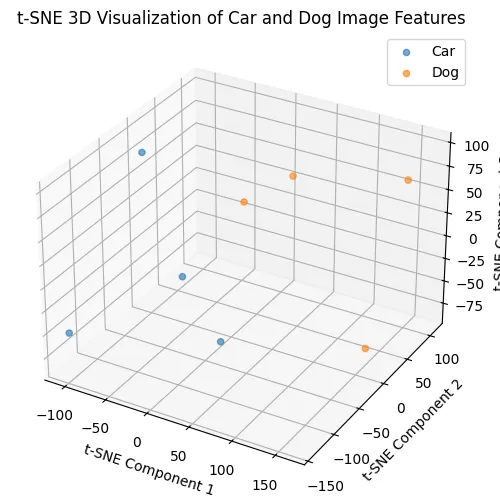
해당 그림은 자동차와 강아지 데이터의 분포입니다. 데이터의 개수가 적어서 확연하게 보이지는 않지만 class별로 다른 데이터의 분포를 갖는 것을 확인할 수 있습니다.
이 예제는 ResNet과 t-SNE를 사용했기때문에 완전한 데이터 분포가아닌, 대략적인 데이터 분포라는점을 참고하시기 바랍니다.
예제를 통해서 비슷한 데이터들은 비슷한 데이터의 분포를 갖는다는 것을 확인했습니다.
하지만 이미지의 분포는 위에서 ResNet과 t-SNE를 사용해서 겨우 시각적으로 보인것이지 사실은 엄청나게 복잡한 분포를 갖고 있습니다.
그렇다면 어떻게 생성모델들은 데이터의 분포를 알면 샘플링을 할 수 있다고 할까요?
Inverse Transform Sampling
Inverse Transform Sampling(역변환 샘플링)은 어떤 확률 분포를 따르는 무작위 변수를 생성하기 위한 기법입니다. 주사위를 예로 들어서 설명해 드리겠습니다.
주사위 예시
주사위를 던졌을 때 1부터 6까지의 숫자가 나오는 확률은 동일합니다. 이렇게 동일한 확률을 가지는 분포를 균등 분포라고 합니다.
Cumulative Distribution Function(CDF, 누적 분포 함수)
CDF는 특정 값 이하의 확률을 나타내는 함수입니다. 예를 들어서, 주사위에서 3이하의 값을 얻을 확률은 각 면이 나올 확률이 1/6이므로 이를 1,2,3의 경우를 모두 더해서 1/2 입니다.
따라서 1일 때는 1/6, 3일때는 1/2(=3/6), 6일 때는 1(=6/6) 이라는 확률을 나타냅니다.
이제 무작위 숫자를 생성하고 CDF에 역으로 적용해서 어떤 주사위 숫자에 해당하는지를 찾아봅시다.
[0,1]까지의 숫자 중에서 0.7이라는 숫자를 선택했을 때, 이는 주사위가 4일 때 0.667(=4/6)과 5일 때 0.833(=5/6)의 사이에 존재하는 값입니다. 따라서 0.7이라는 숫자가 들어왔을 때 숫자를 5라고 지정할 수 있습니다. 사이에 존재할 때 높은 값을 선택하는 이유는 0~1사이의 숫자일 경우 0은 주사위에 존재하지 않기 때문에 자연스러운 결정이라고 보시면됩니다.
이처럼 무작위 숫자를 CDF에 역으로 적용해서 우리가 원하는 특정 값을 찾는 과정을 예시를 통해서 알아봤습니다. 즉 우리는 무작위 숫자로 어떤 값을 샘플링 했다고 보시면 됩니다.
주사위의 예시가 아닌 다른 경우에 우리가 0.7이라는 값을 넣었을 때 어떤 값 사이라는 것을 모르는 상황, 즉 특정 값을 지정 못하는 다른 말로하면 역함수를 구할 수 없는 상황이라면 어떻게 해야할까요?
Rejection Sampling
CDF의 역할수를 구할 수 없는 상황에서 샘플링을 하기 위해 사용되는 방법입니다.

위의 그림에서 검은색 곡선의 분포를 upper bound(q(x))라고 합니다. 즉 검은색 곡선의 위쪽에 아래있는 경우만 허용되고 위쪽에 있는 경우는 허용되지 않습니다. 그래서 곡선안에 있는 동그라미들은 1(허용됨) 밖에 있는 동그라미들은 0(허용되지 않음)을 나타내고 있는 것을 볼 수 있습니다.
우리가 임의의 숫자 0.5를 선택했고 0.5에 해당하는 숫자가 빨간색 선 위에 있을 경우 이를 허용, 파란색 선에 있을 경우 이를 허용하지 않음 으로 분류합니다.
Statistical Perspective for Real Images
2가지 Samples 방법을 통해서 우리가 어떠한 데이터 분포를 안다고 가정했을 때 임의의 특정 값으로 부터 샘플링을 할 수 있음을 확인 했습니다.
이제 데이터의 분포를 학습할 차례입니다. 하지만 처음에 들었던 강아지와 자동차사진처럼 실제 이미지의 분포는 고차원의 복잡한 형태입니다. 따라서 어떠한 간단한 분포로부터 실제 이미지의 복잡한 분포를 학습하는 과정이 Generative Model의 핵심이라고 보시면됩니다.
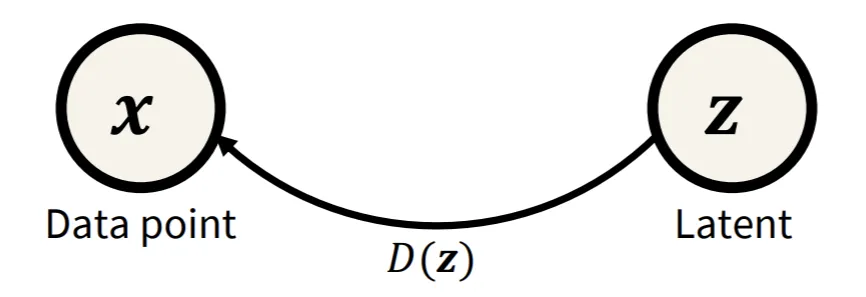
simple distribution(z)로부터 Data point(x)로의 과정을 매핑하는 것을 D(z)라고 합니다.
이렇게 두 분포를 매핑해주는 함수 D를 일반적으로 neural network를 통해서 학습합니다.
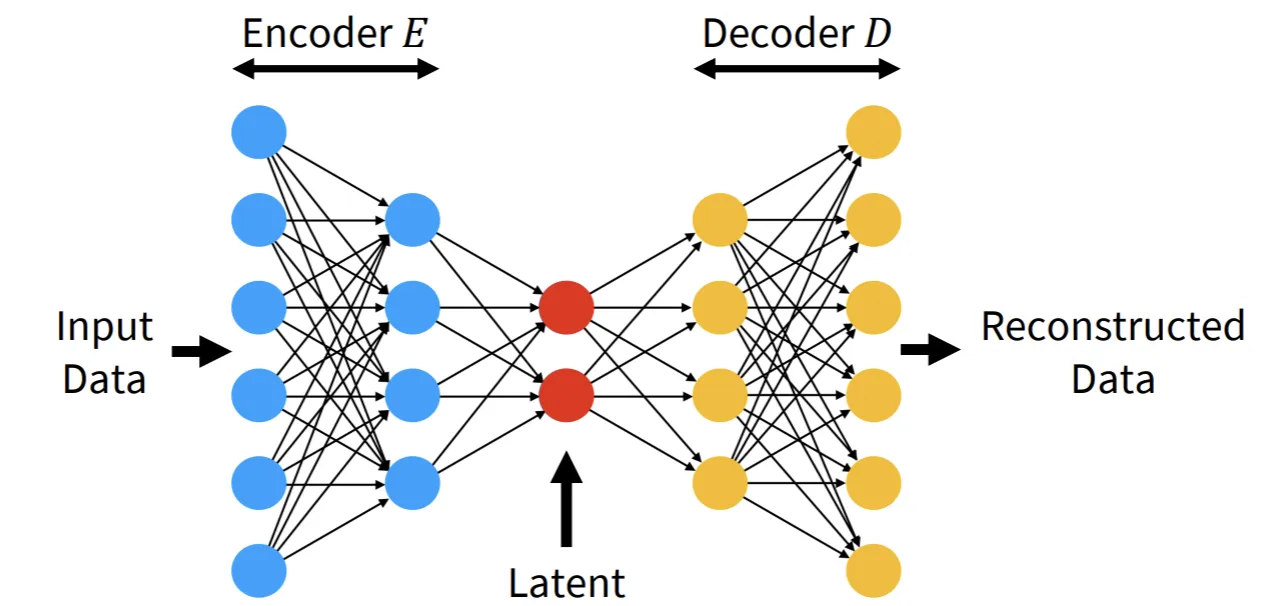
위에서 설명한 함수 D는 AutoEncoder의 Decoder 역할입니다. 간단한 분포는 빨간색 점인 Latent를 의미하고 이를 다시 고차원으로 확장해주는 Decoder를 통해서 일반 이미지의 데이터 분포를 얻을 수 있는 것입니다.
Summary
- 비슷한 데이터들끼리는 비슷한 데이터의 분포를 나타냄
- 샘플링: 임의의 숫자로부터 특정한 값을 얻는 과정
- 생성 모델들은 간단한 데이터 분포에서 복잡한 데이터 분포로 변환
