[한정현 컴퓨터 그래픽스] 17장 매개변수 곡선과 곡면

출처: https://www.youtube.com/watch?v=GoT-gDKlldA&list=PLYEC1V9tJOl03WLDoUEKbiYW_Xt4W6LTl&index=18
한정현님의 컴퓨터그래픽스 17장 강의를 기반으로 제작한 블로그입니다.

Bezier Curve

Quadratic

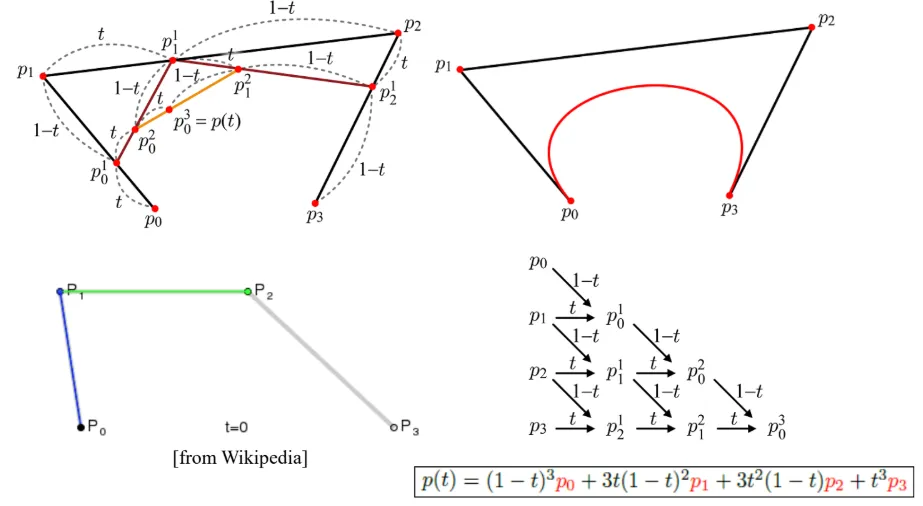
아래 과정은 2차곡선을 정의하기 위해서 interpolation을 recursive하게 진행한 것 입니다.

$p_0$과 $p_1$에 대해서 (t,1-t)의 값을 이용해서 interpolation 값 $p_0^1$을 얻고, 마찬가지로 $p_1$과 $p_2$를 이용해서 interpolation 된 값 $p_1^1$을 얻습니다. 2개의 interpolation된 값을 다시 (t,1-t)를 interpolation하면 마지막으로 $p_0^2$라는 점을 얻고 이렇게 4번의 interpolation을 통해서 점을 구합니다.

t의 값을 0~1까지 진행하게 되면 가운데의 빨간색 곡선이 생성됩니다. 수식은 아래와 같이 interpolation을 통해서 마지막 수식을 얻고, 마지막 수식에 0~1까지의 값을 대입하면 빨간색 곡선이 생성됩니다.

Cubic

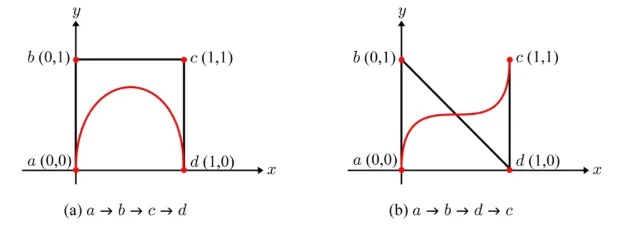
하나의 점을 추가한다면 3차 곡선도 만들 수 있습니다. 더 높은 차원도 충분히 같은 논리로 만들 수 있지만 강의에서는 실제로 많이 쓰이는 3차 곡선까지만 다루기로 했습니다.

Control Points

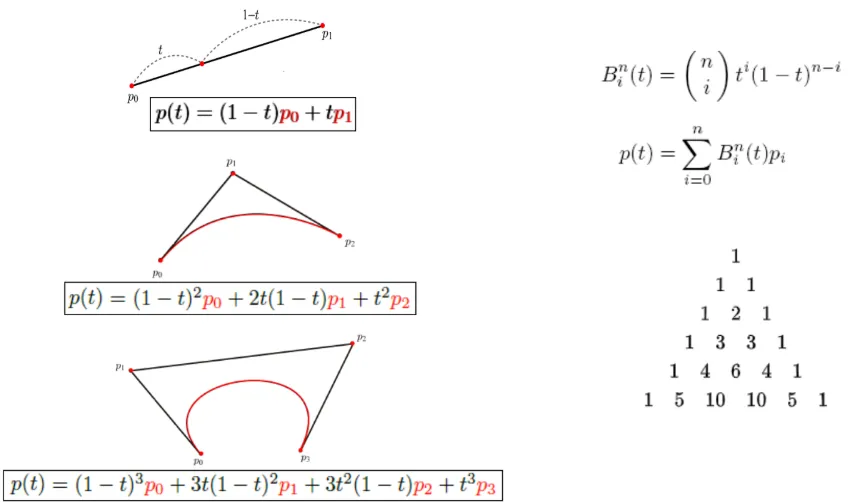
Bezier curve를 만들 때 끝 지점은 무조건 지나고, 가운데 점들은 자신을 향해서 끌어당기기 때문에 점을 지나는 순서가 달라지면 최종적인 결과가 달라지게 됩니다.

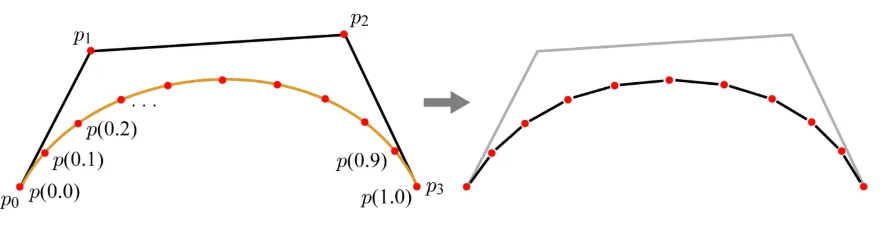
다음으로 수식을 살펴볼건데, 결론적으로 t의 차수는 모든 점들에 대해서 동일해야 합니다. 예를들어서 2차식을 보면 (1-t)가 2차승이면 t는 0차, 가운데 (1-t)가 1차승이면 t는 1차 이런식으로 n차식에 대해서 각 포인트는 t의 n차승이 되어야 합니다.

또한 파스칼 삼각형을 통해서 계수들도 한번에 구할 수 있습니다(오른쪽 그림 참조).

Tessellation

[0,1] 범위에서 t를 10번 샘플링해서 0.1간격으로 각 점들을 구하고, 점들 사이를 선으로 연결하면 대략적인 곡선을 표현할 수 있습니다.

Camera Path

방금 공부한 베이즈 커브를 실제로 Camera path를 구할 때 사용합니다. Camera path는 물체가 고정되어있고 카메라가 곡선을 따라 움직인다고 했을 때 이 곡선을 구하는 방법입니다. Caemra space로 변환하기 위해서 (EYE, AT, UP) 3가지 벡터가 필요한데 AT은 Wordl space상에서 고정, UP도 World space상의 y좌표 방향이기 때문에 EYE 벡터만 변하게 됩니다.

곡선에 따라서 주전자와 구의 위치와 모양이 달라지게 되는 것을 아래 그림을 통해서 확인할 수 있습니다.

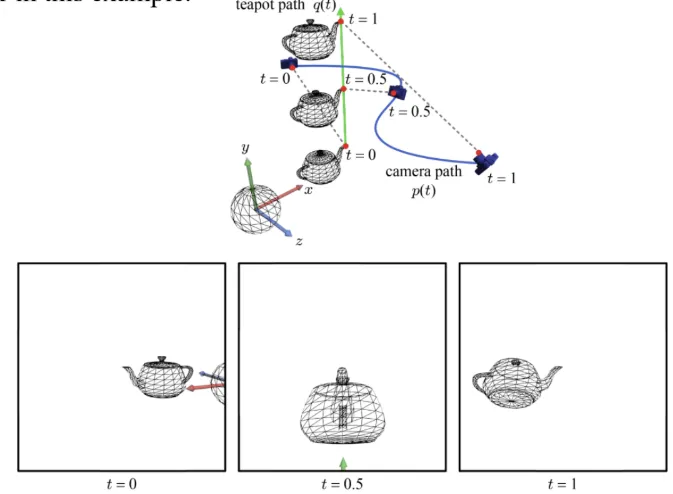
이번에는 EYE뿐만아니라 AT이 주전자의 끝에 달려있으면서 매번 바뀌는 경우를 생각해보겠습니다.주전자가 점점 위로 올라가기 때문에 구가 0초이외의 시각화한 사진에 없는 것을 확인할 수 있습니다.

Bilinear Path

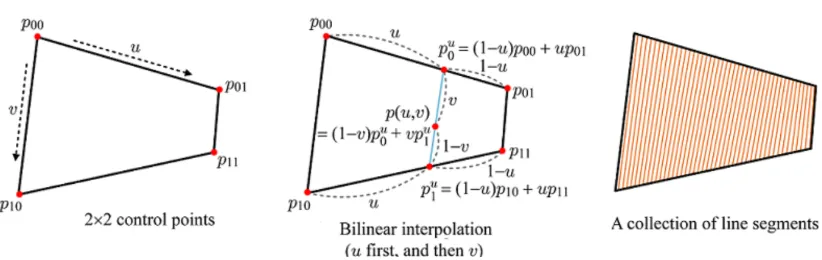
Linear interpolation을 $p_{00}$와 $p_{01}$에 대해서 (u,1-u)로 진행하고, $p_{10}$과 $p_{11}$에 대해서도 (u,1-u)로 진행해서 $p_o^u$와 $p_1^u$를 생성할 수 있습니다. 이때 u의 값을 0~1까지 모두 진행하고 두 점을 잇는다면 맨 오른쪽 그림이 나올 것입니다.

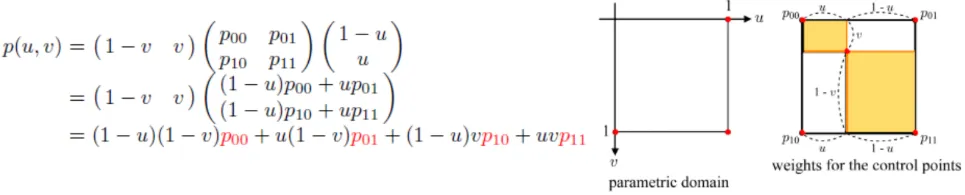
이를 수학적인 행렬로 나타내면 우선 (u,1-u)의 interpolation을 진행하는 과정에 대해서 2번째값과 3번째 값의 행렬곱을 통해서 나타내고, 마지막으로 가운데 점을 찾기 위해서 (1-v,v)를 곱해줘서 최종적으로 bilinear interpolation 결과가 나타납니다. 이를 맨 오른쪽 노란색 넓이를 통해서 시각화 한 것인데, $p_{00}$점이 차지하는 비중은 건너편의 넓이 (1-u)(1-v) 값인 것을 알 수 있습니다.

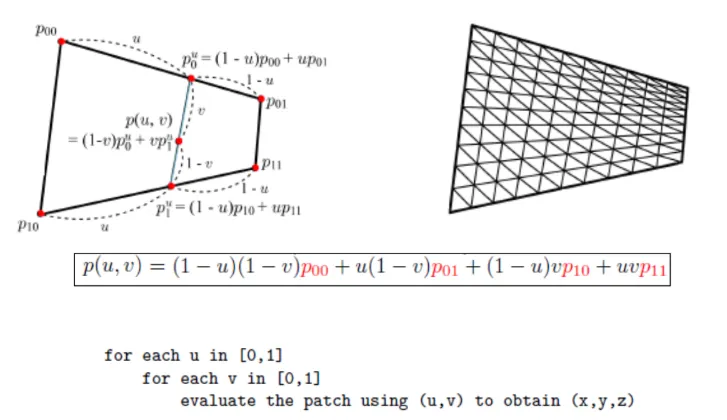
기존에 u의 값을 통해서만 선을 그어서 영역을 나눴는데 v에 대해서도 진행한다면 오른쪽 그림처럼 진행 될 것입니다. 이렇게 되면 가로로 11개의점, 세로로 11개의점 총 121개의 점(좌표)로 나타낼 수 있습니다.

당연히 interpolation의 순서를 바꿔서 v부터 진행하고 u를 진행해도 됩니다. 그럴 경우 위의 그림과 같이 세로로 선들이 나타날 것 입니다.

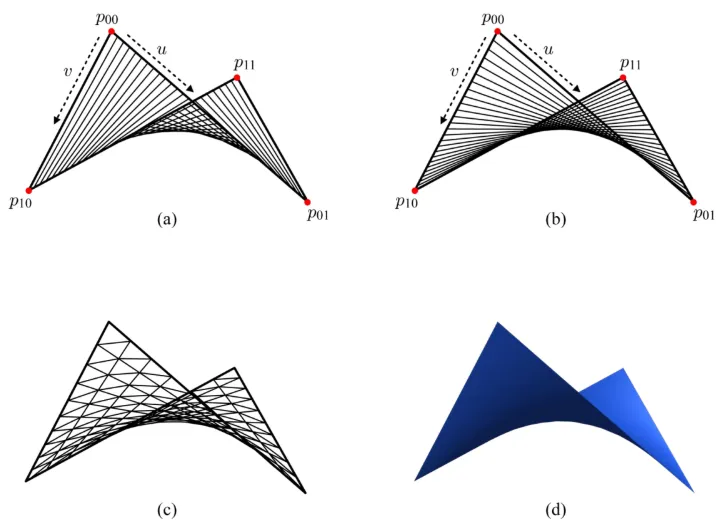
실제로 4개의 점은 한 평면에 존재하지 않고 위의 그림처럼 서로다른 평면에 존재합니다. Bilinear interpolation을 통해서 u,v좌표를 구하고 texturing과 shadow를 추가한 렌더링 결과는 (d)와 같습니다. 약간은 평면같이 느껴진다는 단점이 존재합니다.

따라서 control point의 개수를 4개에서 9개로 늘려서 2차 bazier curve를 이용해서 더 곡면스러운 형태를 나타낼 수 있습니다. 이를 Biquadratic Bezier Patch라고 합니다.

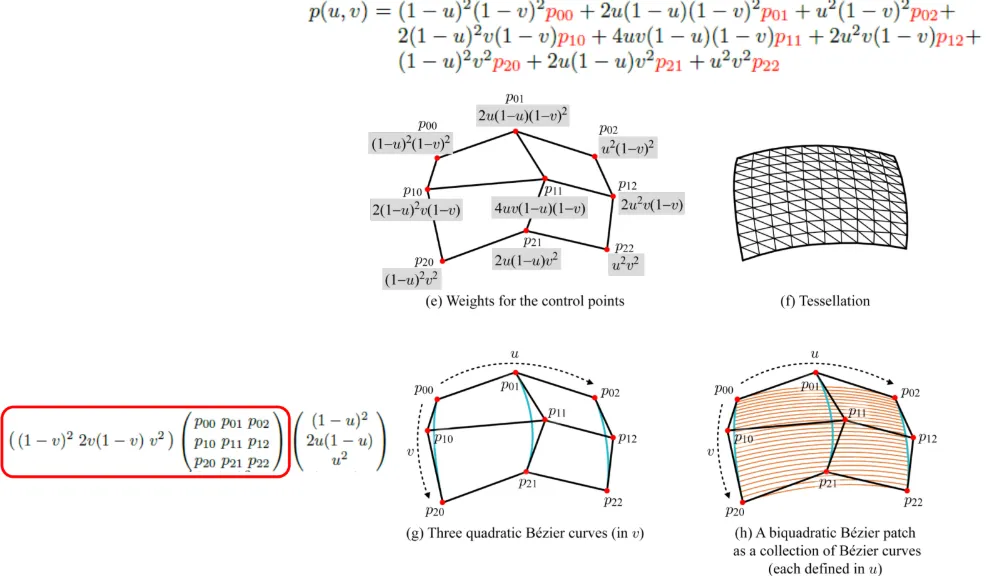
이전과 똑같이 u와 v의 여러 조합을 통해서 좌표를 얻는 과정을 진행 할 수 있습니다. u와 v를 먼저하는 순서에 따라서 이전처럼 세로로 주황색 선이 나타날 수도 있고, 아니면 위의 그림처럼 가로로 주황색 선이 나타날 수도 있습니다.