MAB(Multi-armed Bandit)

구국원·2020년 5월 17일

MAB를 이해하기 위해 필요한 베타분포(beta), 이항분포(binomial), 베이지안 추정, 톰슨 샘플링과 관련된 내용을 정리하겠습니다.

1 A/B 테스트 자동화의 필요성

캠페인을 진행하면서, 어떤 배너가 더 높은 구매 전환율을 유도하는지를 알기 위해 배너별 노출 비율을 수동으로 설정할 수 있습니다. 그 비율은 처음 설정되면, 테스트가 끝날때까지 고정됩니다.

만일 테스트 종료 후 A 배너가 B배너 보다 높은 구매 전환율을 유도하는 것으로 결론이 났다면, 우리는 A 배너를 노출하는 의사결정을 하게됩니다.

그런데 그러한 결론을 유도하는 과정에서 구매 전환율이 낮다고 결론난 B 배너를 일정 비율로 계속 노출해야하므로 이에 따른 손실이 발생하게 됩니다. A 배너를 더 많이 노출 했으면 더 높은 수익을 얻을 수 있었을 텐데 말이죠.

만일 A 배너와 B 배너의 노출 비율을 상황에 적합하게 실시간으로 조정할 수만 있다면, 배너 노출 테스트하는 기간 동안의 기회비용을 줄일 수 있을 것 같습니다. 이 시점에서 MAB의 필요성이 등장하게 됩니다.

2 MAB에 필요한 분포

2.1 분포의 필요성

우리는 서비스를 진행하면서 어떤 배너에 대해 노출수와 구매건수 얻을 수 있습니다. 또한 단순한 사칙연산을 통해서 구매 전환율을 얻어 낼 수 있죠. 그런데 그렇게 해서 얻어낸 구매 전환율이 실제 모수를 대표한다고 확신할 수 있을까요? 저희가 얻은 데이터는 '표본'에 불과하기 때문에, 단순한 표본 통계량으로는 이것이 모수를 대표한다고 단정지어 말할 수 없겠습니다.

그렇다면 얻어진 구매 전환율이 어느정도의 신뢰도 혹은 확신도로 실제 모수를 반영하고 있는지를 '정량적' 지표로 나타낼 수 없을까요? 이는 베타분포(beta)와 이항분포(binomial)를 통해서 이끌어 낼 수 있습니다.

결론부터 말하자면 사전확률분포와 데이터 발생 분포를 각각 베타분포, 이항분포로 가정하면, 사후확률분포도 베타분포임을 도출할 수 있습니다. 베타분포는 2개의 모수 $\alpha, \beta$ 를 통해 분포의 모양을 비교적 자유롭게 바꿀 수 있으며, 확률변수가 0~1사이의 실수값이므로, '구매 전환율'의 신뢰도를 나타내기의 안성맞춤인 분포이죠.

2.2 사전 분포: 베타분포(beta distribution)

베타분포는 $RV = \theta(\in [0,1])$ 을 가지는 분포를 말합니다. 여기서 $\theta$ 는 0~1사이의 실수값을 가지므로, 확률로 해석할 여지가 있습니다. $\theta$ 를 구매 전환율로 볼때, 표본 데이터를 통해 도출한 전환율이 실제 모수임을 어느 정도의 확신 혹은 신뢰할 수 있는지를 이끌어 낼 수 있습니다.

\begin{aligned} Beta(\alpha, \beta) &= f(\theta; \alpha, \beta) = P(\theta; \alpha, \beta) \\\\ &= \cfrac{\theta^{\alpha-1}(1-\theta)^{\beta-1}}{B(\alpha, \beta)}\space, \theta \in [0, 1] \\\\ &=\cfrac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}\space\theta^{\alpha-1}(1-\theta)^{\beta-1} \end{aligned}

B(\alpha, \beta) = \int_{0}^{1}\theta^{\alpha-1}(1-\theta)^{\beta-1}d\theta = \cfrac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}

2.3 데이터 분포: 이항분포(binomial distibution)

이항분포는 독립적인 베르누이 시행에 대한 연속 확률 분포(continuous distribution)입니다. 이항분포의 RV는 독립적인 베르누이 시행을 n번 시행했을 때의 성공 횟수를 뜻합니다.

n번 시행에서 성공 횟수(구매 횟수)가 k인 이항분포의 pdf는 다음과 같습니다.

\begin{aligned} P(X=k|\theta) &= B(n, \theta)\\ &=\binom{n}{k} \theta^{k}(1-\theta)^{n-k} \end{aligned}

이항분포에 왜 조합(combination)이 있을까요? 독립적인 동전 던지기 시행을 5번 했을 때, 2번 성공(=앞면이 나옴) 했을 때를 가정해봅시다. 첫번째, 세번째에서 동전의 앞면이 나왔을 때와 두번째 다섯번째에서 동전이 앞면이 나오는 경우는 모두 같은 확률을 나타냅니다. 다시말해, 5개 중 2개를 순서와 상관없이 뽑는 경우에 대응되는 확률을 모두 고려해 주어야 하기 때문에 조합을 사용합니다.

2.4 사후 분포: 베타분포(beta distribution)

사후 분포는 사전 분포인 베타분포 $\big(P(\theta)\big)$ 와 데이터 분포인 이항분포 $\big(P(k)\big)$ 의 조건부 결합 확률 밀도 함수(joint probability density function)으로로 나타낼 수 있습니다. 결합 확률 밀도 함수에 대한 자세한 내용은 이곳을 참조해 주세요.

\begin{aligned} P(\theta|X=k) &= \cfrac{P(X=k|\theta)P(\theta)}{P(X=k)} \\\\ &=\cfrac{P(X=k|\theta)P(\theta)}{\int_{0}^{1} P(X=k|\theta)P(\theta)d\theta} \\\\ &= \cfrac{P(X=k|\theta)P(\theta)}{\int_{0}^{1} P(X=k|\theta)P(\theta)d\theta} \\\\ &= \cfrac{\dbinom{n}{k} \theta^k(1-\theta)^{(n-k)}{\cfrac{\theta^{\alpha-1}\theta^{\beta-1}}{B(\alpha, \beta)}}}{\int P(k|\theta)P(\theta)d\theta} \\\\ &= \cfrac{\dbinom{n}{k}{\cfrac{\theta^{(\alpha+k)-1}\theta^{(\beta+n-k)-1}}{B(\alpha, \beta)}}}{\int_{0}^{1} P(X=k|\theta)P(\theta)d\theta} \\\\ &= \cfrac{\dbinom{n}{k}{\cfrac{\theta^{(\alpha+k)-1}\theta^{(\beta+n-k)-1}}{B(\alpha, \beta)}}}{\int_{0}^{1}\dbinom{n}{k}\theta^{k}(1-\theta)^{n-k} \cfrac {\theta^{\alpha-1}\theta^{\beta-1}} {B(\alpha, \beta)} } \\\\ &= \cfrac{\dbinom{n}{k}{\cfrac{\theta^{(\alpha+k)-1}\theta^{(\beta+n-k)-1}}{B(\alpha, \beta)}}}{\dbinom{n}{k} \cfrac{1}{B(\alpha, \beta)}\int_{0}^{1}\theta^{k}(1-\theta)^{n-k} \theta^{\alpha-1}\theta^{\beta-1}} \\\\ &= \cfrac{\dbinom{n}{k}{\cfrac{\theta^{(\alpha+k)-1}\theta^{(\beta+n-k)-1}}{B(\alpha, \beta)}}}{\dbinom{n}{k} \cfrac{1}{B(\alpha, \beta)}\int_{0}^{1}\theta^{\alpha+k-1}(1-\theta)^{\beta+n-k-1}} \\\\ &= \cfrac{\dbinom{n}{k}{\cfrac{\theta^{(\alpha+k)-1}\theta^{(\beta+n-k)-1}}{B(\alpha, \beta)}}}{\dbinom{n}{k} \cfrac{B(\alpha+k, \beta+n-k)}{B(\alpha, \beta)}} \\\\ &= \cfrac{1}{B(\alpha+k, \space \beta+n-k)} \space \theta^{(\alpha+k)-1}(1-\theta)^{(\beta+n-k)-1} \\\\ &= Beta(\alpha+k, \space \beta+(n-k)) \end{aligned}

참고로 $P(X=k)$ 는 결합확률분포의 관점에서는 marginal probability이므로, 전확률의 법칙에 따라 아래와 같이 쓸수 있습니다.

\begin{aligned} P(k) &= \int P(X=k, \theta)d\theta \\ &= \int P(X=k|\theta)P(\theta)d\theta \end{aligned}

사후 분포도 역시 베타 분포임을 알 수 있습니다!!

2.5 켤레 사전 확률 분포(conjugate prior distribution)

켤레 분포란, 모수는 다르지만, 사전 분포와 사후 분포의 형태를 같게 하는 사전 분포를 뜻합니다.

사전분포와 데이터 분포를 각각 베타분포, 이항분포로 가정했을 때, 사후분포는 베타분포이므로 사전분포는 켤레 사전 확률 분포라고 할 수 있습니다.

3 톰슨 샘플링(Thomson Sampling)

톰슨 샘플링이란, 도출된 베타 분포에서 RV(e-commerce에서는 일반적으로 전환율)를 샘플링하는 기법을 말합니다. 배너 $i$ 의 conversion 횟수, expression 횟수를 알고 있으면, $\alpha_{i}$ 와 $\beta_{i}$ 를 다음과 같이 정의할 수 있고 이 두가지 모수만 있으면 각 배너의 베타분포를 그릴 수 있습니다.

\begin{aligned} \alpha_{i} &= 배너 \space i의 \text {\space conversion \space 횟수} = \text{conversion \space 성공 \space 횟수}\\ \beta_{i} &= 배너 \space i의 \text{\space expression \space 횟수} - \text{conversion \space 횟수} = \text{conversion \space 실패 \space 횟수} \end{aligned}

배너 A는 expression 13회, conversion 4회. 배너 B는 expression 11회, conversion 5회라면 각 배너의 베타 분포는 아래와 같이 나타납니다.

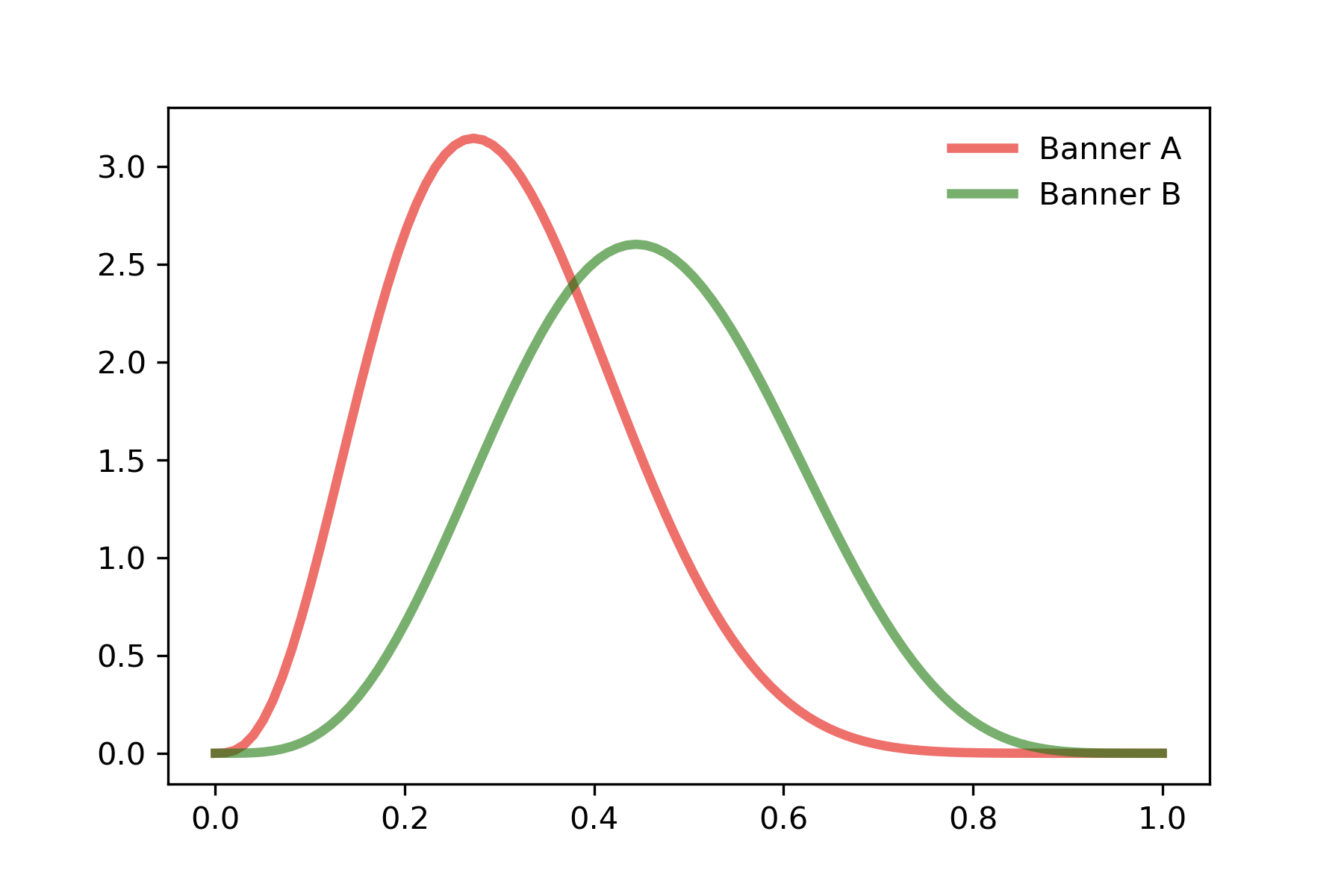
여기서 배너 A와 배너 B의 conversion rate의 기댓값을 뽑아서 기댓값이 높은 배너를 노출 시키는 전략을 취하면 될 것 같습니다. 배너 A의 conversion rate 기댓값은 0.307, 배너 B의 conversion rate 기댓값은 0.454입니다. 따라서 우리는 배너 B만 계속 노출시키면 되겠군요.

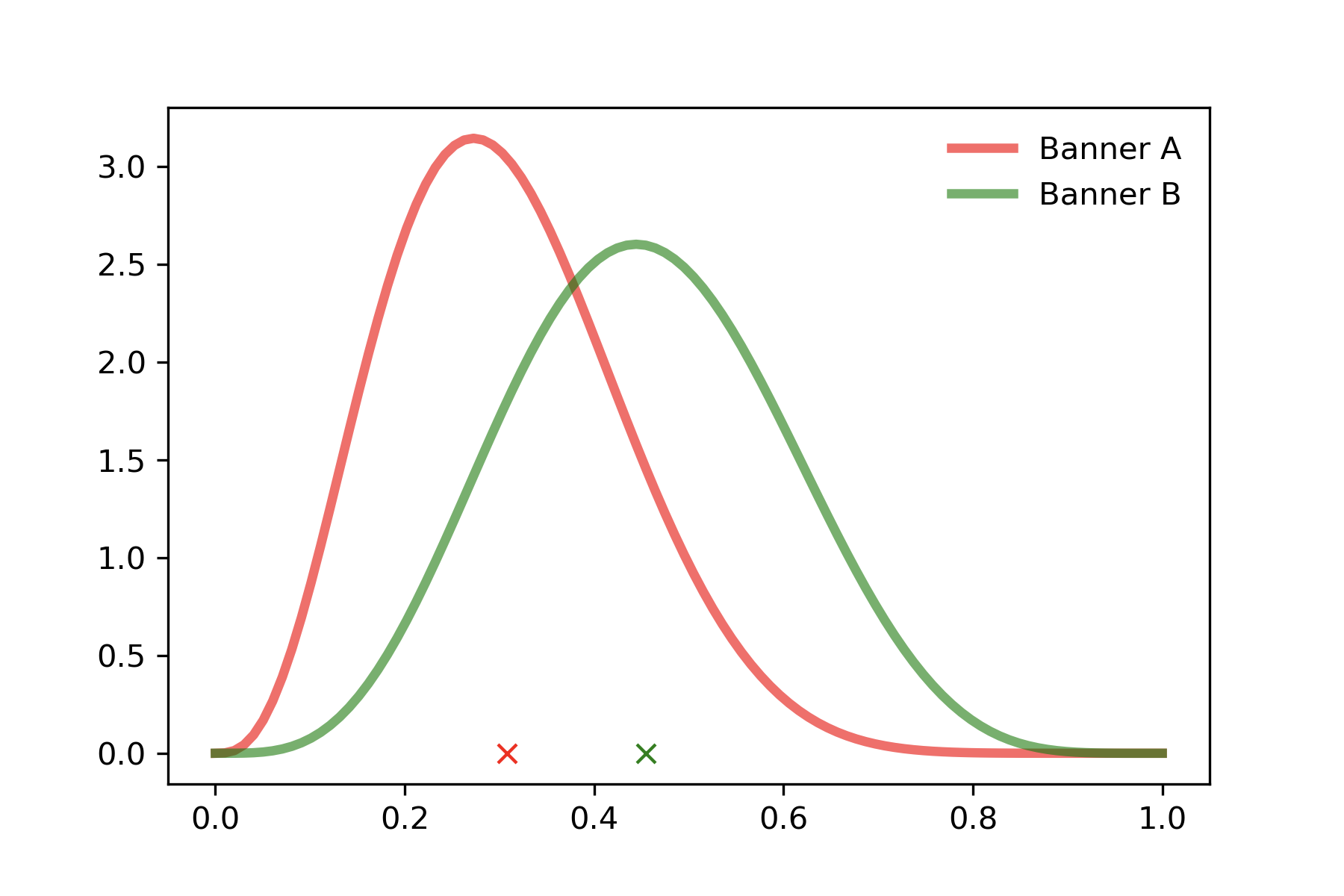
그러나 한번만 더 생각 해봅시다. conversion rate의 기댓값이 높은 배너만 계속해서 노출시키는 것이(greedy) 항상 최선을 결과를 보장할까요? 배너 B가 배너 A에 비해 어느 시점에서는 기댓값이 높을 수는 있습니다. 그러나 이러한 현상이 '우연히' 발생 했을 수도 있지 않을까요? 우리는 배너 A에 대한 충분한 탐색(exploration)을 하지 못했습니다.

따라서 우리는 exploitation과 exploration을 적절히 섞어서 A/B 테스트를 진행하여야 하겠습니다. 이때 톰슨 샘플링이라는 간단한 알고리즘을 활용합니다. 톰슨 샘플링은 베타 분포에서 RV를 샘플링하기 때문에, exploitation과 exploration의 효과를 누릴 수 있습니다.

톰슨 샘플링 결과 배너 A에서는 0.337, 배너 B에서는 0.271가 샘플링 되었습니다. 배너 A의 conversion rate 기댓값이 더 낫지만, 현재 시점에서는 샘플링 된 conversion rate가 더 큰 배너 A를 노출 시키는 전략(exploration)을 취하면 되겠습니다.

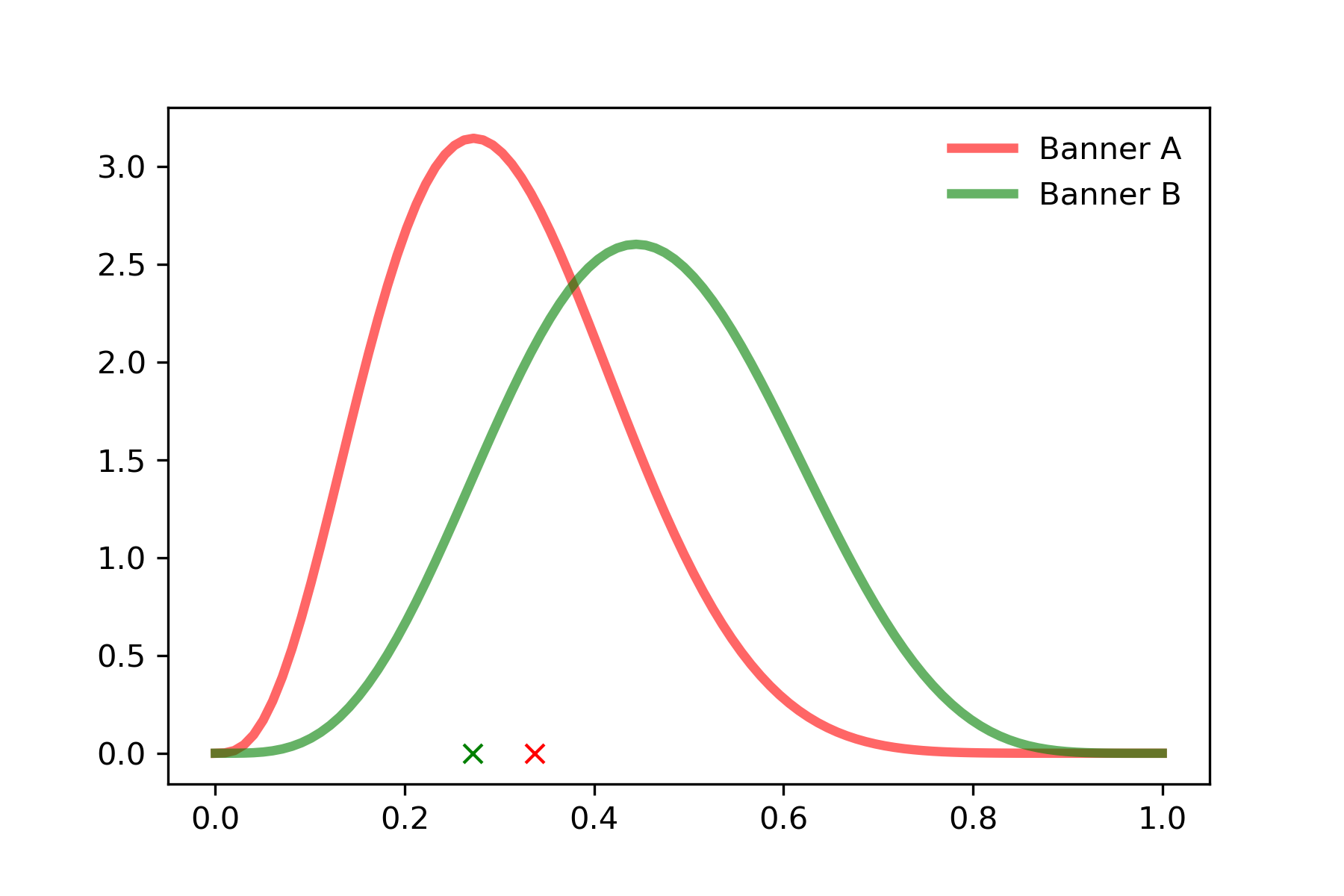
결과적으로 N개의 배너 당 2개의 값(conversion 횟수, expression 횟수)만 계속 저장 및 업데이트하면, 베타 분포와 톰슨 샘플링 알고리즘을 통해 적절한 exploration과 exploitation을 진행하여 최적의 배너를 자동으로 노출 시킬 수 있게 됩니다.