"Attention Is All You Need" Review

구국원·2020년 6월 16일

NLP positional encoding self-attention transformer

"Attention Is All You Need" 논문을 읽은 후 관련 자료를 정리한 내용을 바탕으로 논문 리뷰를 진행 해보겠습니다.

1 Introduction

2 Background

3 Model Architecture

transformer에서 가장 중요한 block은 self-attention과 point-wise feed forward network sub-layer입니다. 인코더와 디코더 셀 하나는 self-attention 및 point-wise feed forward network 2개로 구성되어 있습니다. 각 sub-layer는 residual connection와 layer batch normalization으로 연결되어 있습니다.

3.1 Encoder and Decoder Stacks

Transformer imitates the classical attention mechanism (known e.g. from Bahdanau et al., 2014 or Conv2S2) where in encoder-decoder attention layers queries are form previous decoder layer, and the (memory) keys and values are from output of the encoder. Therefore, each position in decoder can attend over all positions in the input sequence.

Decoder acts similarly generating one word at a time in a left-to-right-pattern. It attends to previously generated words of decoder and final representation of encoder.

3.2 Positional Encoding

transformer는 sequence token의 sequence 정보를 알 수 없으므로, 순서 정보를 주입(inject) 시켜주어야 합니다.

3.3 Scaled Dot-Product Attention

\begin{aligned} Attention(Q, K, V) = softmax\Bigg(\cfrac{QK^{T}}{\sqrt{d_{k}}}\Bigg)V \end{aligned}

왜 $\sqrt{d_{k}}$ 로 나누어 줄까요? $d_{k}$ 가 커짐에 따라 dot-product가 너무 커져버리는 효과를 상쇄하기 위함입니다. 예를 들어 아래의 두 벡터를 비교해봅시다.

\begin{aligned} \vec{a} &=[2, 2], \space where \space d_{k}=2 \\ \vec{b} &=[2, 2, 2, 2, 2], \space where \space d_{k}=5 \\ \end{aligned}

\begin{aligned} \vec{a} \cdot \vec{a} &= 8\\ \vec{b} \cdot \vec{b} &= 20, \end{aligned}

$d_k$ , 즉 임베딩 차원이 길 수록, dot-product 값은 커지는 필연적인 결과가 나타납니다. dot-product 값이 커지면 어떤 문제가 생길까요? 결론적으로 말하면 특정 노드의 softmax값이 1에 수렴하게 되어 gradient가 매우 작아지므로 초기 학습시에 문제가 발생할 여지가 있습니다. 저자는 논문에 이렇게 표현하고 있습니다.

We suspect that for large values of $d_{k}$ , the dot products grow large in magnitude, pushing the softmax function into regions where it has extremely small gradients . To counteract this effect, we scale the dot products by $\cfrac{1}{\sqrt{d_{k}}}$

간단하게 코드로 알아봅시다. $0.3$ 과 $0.4$ 두 개의 원소를 가지고 있는 $d_{k}=2$ 인 $\vec{v_{1}}$ 를 만들고 softmax 함수의 값을 구해봅시다.

[In]:
v1 = np.array([0.3, 0.4])
print(np.exp(v1)/np.sum(np.exp(v1)))

[Out]: 
array([0.47502081 0.52497919])

이제 $\vec{v_{1}}$ 의 각 원소에 100을 곱한 $\vec{v_{2}}$ 에 역시 softmax 함수를 통과한 값을 구해봅시다. $\vec{v_{1}}$ 과 $\vec{v_{2}}$ 는 절대적 크기는 달라졌지만, 상대적 크기는 달라지지 않았다는 점을 유념해 주시기 바랍니다.

[In]:
v2 = v1 * 100
print(np.exp(v2) / np.sum(np.exp(v2)))

[Out]:
array([4.53978687e-05 9.99954602e-01])

결과를 보면, 원소의 magnitude가 큰 벡터에 softmax를 씌웠을 때는 1에 수렴하는 값이 발생함을 할 수 있습니다. 따라서 초기에 학습이 잘 이루어지기 위해서는 gentle한 softmax 값을 얻어낼 필요가 있다는 것을 알 수 있습니다. 큰 softmax 값에 대해서는 graident가 매우 작아 역전파시 전달되는 값이 거의 0에 가깝기 때문입니다.

왜 softmax 값이 크면 전달되는 gradient가 작아질까요(small gradient problem)? 먼저 notation을 정의합시다.

\begin{aligned} z_j &= element_{j}\text{ of output vector}\\ y_i &= \cfrac {e^{z_i}} {\sum_{k}e^{z_i}} \end{aligned}

softmax 함수에 대한 미분을 구하면 아래와 같습니다(자세한 계산 과정은 Appendix를 참조해 주세요).

\cfrac {\partial {y_{i}}} {\partial {z_{j}}} = \begin{cases} y_{i}(1-y_{i}) &\text{if } i=j \\ -y_{i}y_{j} &\text{if } i\not=j \end{cases}

만약 $i=j$ 이고, $y_i$ 의 값이 1에 가깝다면, gradient는 0에 가까운 값이 전달 됩니다. 한편 $i \not = j$ 이고 $y_i$ 의 값이 1에 가깝다면, $y_j$ 는 0에 가까운 값이므로 역시 gradient 값이 매우 작아질 것입니다. 이러한 현상이 학습 말미에 벌어진다면 학습이 잘 되었다는 증거로 생각할 수 있겠으나, 학습 초기부터 small gradient 문제가 발생한다면 학습이 정상적으로 이루어지지 않을 것이라는 것을 미루어 짐작할 수 있습니다. 따라서 학습 초기에는 gentle softmax를 만드는 것이 중요하므로 $\sqrt d_k$ 로 나누어 주는 것입니다.

3.4 Multi-Head Attention

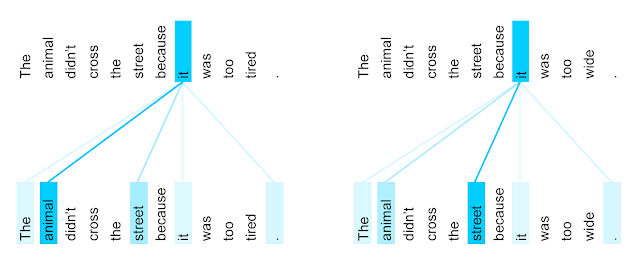
The encoder self-attention distribution for the word “it” from the 5th to the 6th layer of a Transformer trained on English to French translation (one of eight attention heads).