2. 데이터

2-1. 0과 1로 숫자를 표현하는 방법

[목표]

• 정보단위에 대해 알아보자!
• 0과 1만으로 숫자를 표현하는 방법을 알아보자!

정보 단위

• 비트(bit) : 가장 작은 정보 단위 (전구 하나 : 꺼짐=0 / 켜짐=1)

  • $n$ 비트는 $2^n$ 가지 정보를 표현

    단위	크기
    1바이트(1byte)	8비트(8bit)
    1킬로바이트(1kB)	1,000바이트(1,000byte)
    1메가바이트(1MB)	1,000킬로바이트(1,000kB)
    1기가바이트(1GB)	1,000메가바이트(1,000MB)
    1테라바이트(1TB)	1,000기가바이트(1,000GB)

• 워드(word) : CPU가 한 번에 처리할 수 있는 데이터 크기
  • 예) CPU가 한 번에 16비트를 처리할 수 있다면 1워드는 16비트가 되고,
    한 번에 32비트를 처리할 수 있다면 1워드는 32비트가 되는 것
  • 현대 컴퓨터의 워드 크기는 대부분 32비트 또는 64비트
  • 인텔의 x86 CPU는 32비트 워드 CPU, x64 CPU 는 64비트 워드 CPU
    
    
    

이진법(binary)

[이진수 표기]

• 수학적 표기 : $1011_{(2)} = 8$
• 코드에서 표기 : $0b1011$

[이진수 음수 표현]

• 2의 보수(two’s complement) 값을 음수로 간주함
  • 사전적 정의 : 어떤 수를 그보다 큰 $2^n$에서 뺀 값
    • 예) $11_{(2)}$의 2의 보수 : $100_{(2)} - 11_{(2)} = 01_{(2)}$
  • 쉬운 계산 방법 : 어떤 수를 반대로 뒤집고 1 더하기
    • 예) $11_{(2)} \rightarrow 00_{(2)} \rightarrow 01_{(2)}$

[🙋🏻‍♀️ 질문!] 3을 음수로 표현한 3의 2의 보수 식 $01_{(2)}$ 과 실제 1의 이진수가 같은 표현인데, 3의 음수인지 어떻게 알죠?

• 컴퓨터 내부에서 양수인지 음수인지 구분하기 위해 플래그(flag) 사용
  

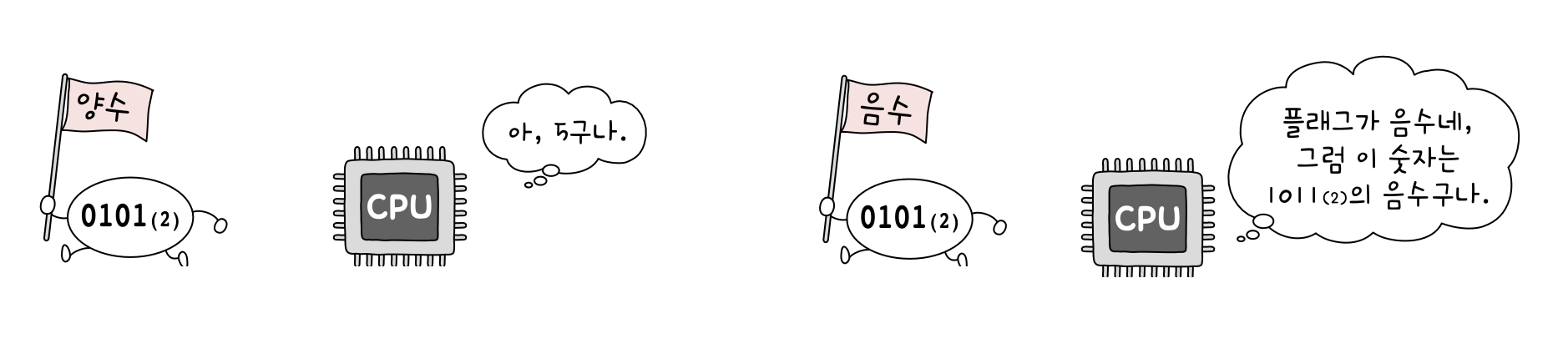
[2의 보수 표현의 한계]

• $0$ 이나 $2^n$ 형태의 이진수에 2의 보수를 취하면 원하는 음수값을 얻을 수 없다.

십육진법(hexadecimal)

[십육진수 표기]

• 수학적 표기 : $15_{(16)} = 21$
• 코드에서 표기 : $0$x$15$

[십육진수를 이진수로 변환하기]

• 십육진수를 이루는 숫자 하나를 이진수로 표현하려면 4비트가 필요
• 십육진수 한 글자를 4비트의 이진수로 간주
• 각 글자를 따로따로 이진수로 변환
  

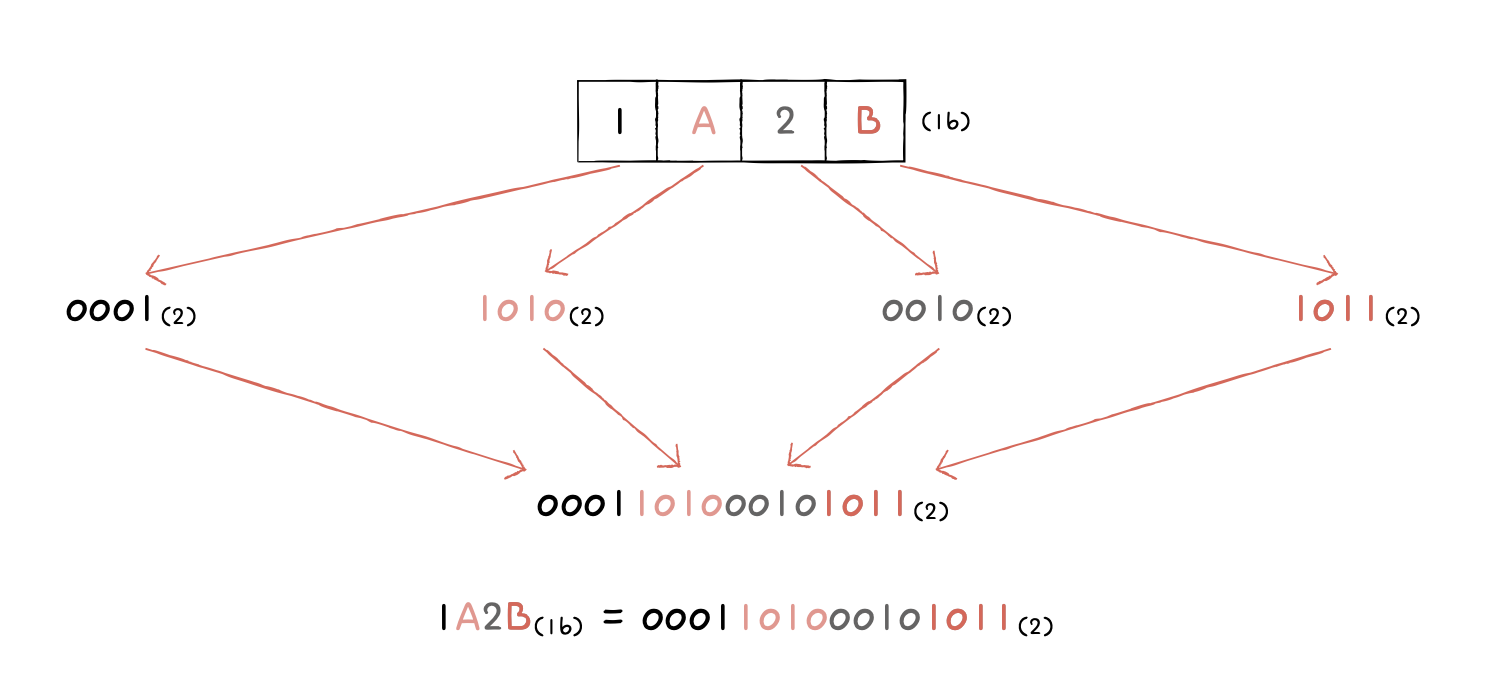
[십육진수를 이진수로 변환하기]

• 이진수 숫자를 네 개씩 끊고, 끊어 준 네 개의 숫자를 하나의 십육진수로 변환한 뒤 그대로 이어 붙임
  

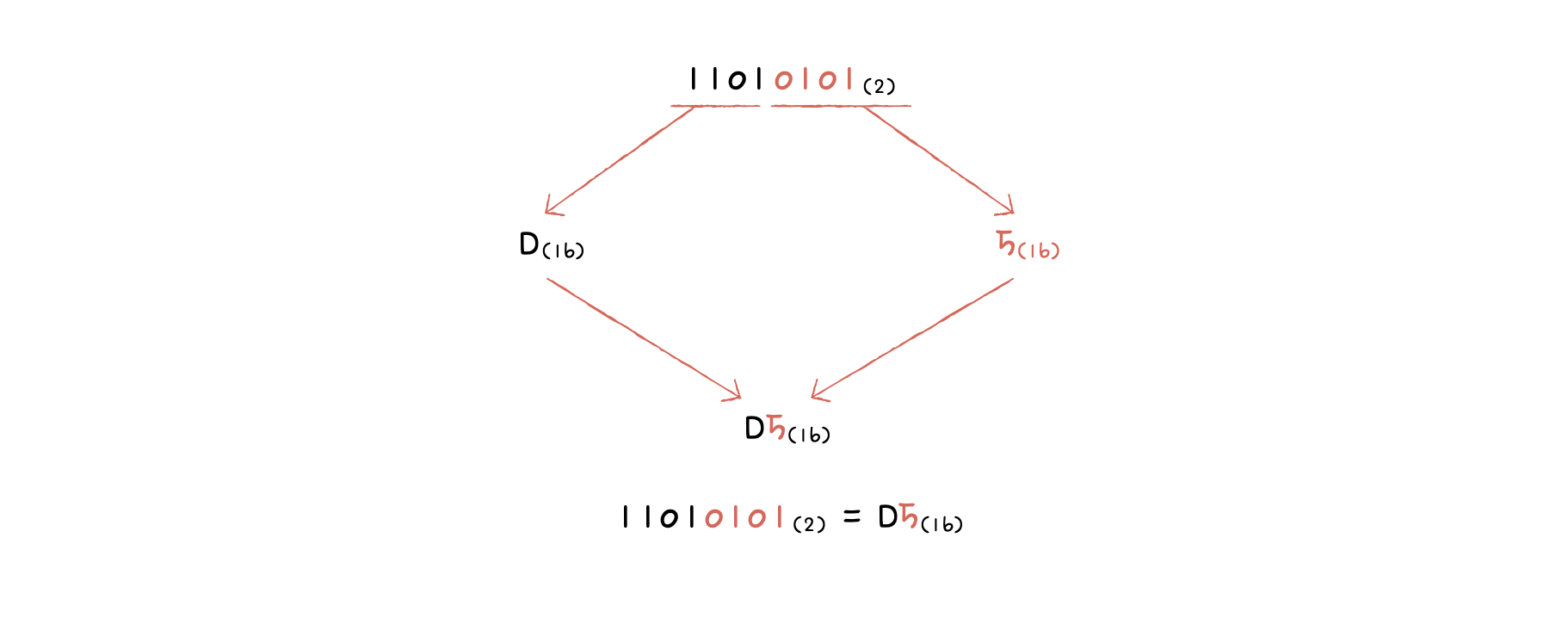
[⭐️혼공단 미션 인증!⭐️]

p.65-3번 문제 : $1101_{(2)}$ 의 음수를 2의 보수 표현법으로 구하면, $0011_{(2)}$ 이다.

• [풀이과정] $1101_{(2)} \rightarrow 0010_{(2)} \rightarrow 0011_{(2)}$

2-2. 0과 1로 문자를 표현하는 방법

[목표]

• 컴퓨터가 문자를 이해하고 표현하는 다양한 방법에 대해 알아보자!

문자 집합과 인코딩

☝🏻0과 1로 문자를 표현하는 방법에 대해 알아보기 전 반드시 알아야 할 세 가지 용어

• 문자 집합(character set) : 컴퓨터가 인식하고 표현할 수 있는 문자의 모음
• 문자 인코딩(character encoding) : 문자를 0과 1로 변환하는 과정, 인코딩 후 0과 1로 이루어진 결과값이 문자 코드
• 문자 디코딩(character decoding) : 문자 코드를 사람이 이해할 수 있는 문자로 변환하는 과정

아스키코드(ASCII; American Standard Code for Information Interchange)

[참고] https://ko.wikipedia.org/wiki/ASCII

• 한글 표현이 없음
• 더 다양한 문자 표현을 위해 아스키 코드에 1비트를 추가한 8비트의 확장 아스키(Extended ASCII)가 등장하기도 했지만, 턱없이 부족

EUC-KR

[참고] https://ko.wikipedia.org/wiki/EUC-KR

• 한글 인코딩 2가지 방식 (완성형, 조합형) 중 완성형
• 모든 한글 조합 표현 못함
• '쀍', '쀓', '믜' 같은 단어들의 깨짐 발생

CP949(Code Page 949)

[참고] https://en.wikipedia.org/wiki/Unified_Hangul_Code

• 한글 깨짐 문제를 조금이라도 해결하기 위한 EUC-KR의 확장된 버전
• 마이크로소프트 제작
• 여전히 부족...

유니코드와 UTF-8

[참고] https://en.wikipedia.org/wiki/Category:Unicode_charts
[참고] https://www.unicode.org/charts/PDF/UAC00.pdf

• 모든 나라 언어의 문자 집합과 인코딩 방식이 통일된 문자 집합
• 현대 문자를 표현할 때 가장 많이 사용되는 표준 문자 집합
• 글자에 부여된 값 자체를 인코딩된 값으로 삼지 않고 이 값을 다양한 방법으로 인코딩
  • UTF-8, [참고] https://ko.wikipedia.org/wiki/UTF-8
  • UTF-16,
  • UTF-32 등