Description
Given a non-empty array of integers nums, every element appears twice except for one. Find that single one.
You must implement a solution with a linear runtime complexity and use only constant extra space.
Example 1:
Input: nums = [2,2,1]
Output: 1Example 2:
Input: nums = [4,1,2,1,2]
Output: 4Example 3:
Input: nums = [1]
Output: 1Solution
비트 연산이 익숙하지 않았는데... 이렇게 하는 거였다니, 신세계다.
기본적으로 XOR이라고 불리는 비트 배타적 논리합 연산자를 사용하면 된다.
이에 대해 잘모르겠다면 별도로 포스팅해두었으니 참고해도 좋을 것 같다.
/**
* @param {number[]} nums
* @return {number}
*/
var singleNumber = function(nums) {
return nums.reduce((accum, num) => {return accum^num},0)
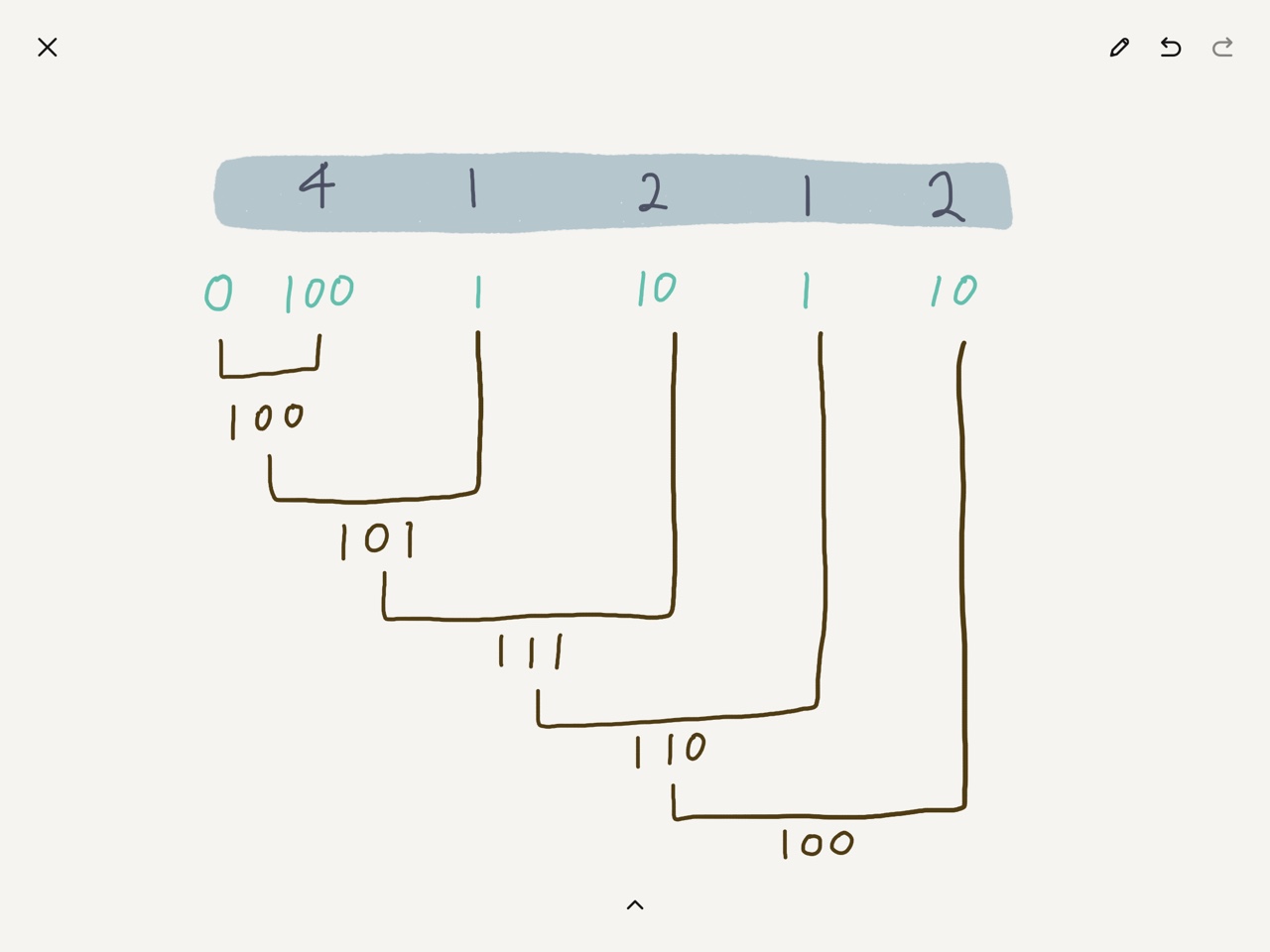
};원리는 다음과 같다. (아래 이미지 참고)
초기값 0과 4를 XOR로 누산하고, 반복한다.
여기서 중요한 부분은 배열의 모든 요소는 2의 배수이기 때문에 1이 하나만 들어있는 이진수로 표현 가능하다.
예를들어,
1 => 1
2 => 10
4 => 100
8 => 1000따라서 XOR로 연산할 때 각 자리의 수가 겹치지 않아 1이 계속 겹치며 쌓인다.
예를 들면,
4를 이진수로 나타냈을 때 100이다.
4애 8을 연산하면
4^8 => 100^1000 => 1100
여기에 다시 2를 연산하면
1100^10 =>1110그리고 중복된 같은 2의 배수가 2개씩 들어있으면, 남은 동일한 2의 배수를 다시 연산했을때
겹쳐 더해졌던 1일 빠져 0이 된다.
예를들어,
1110에서 2를 다시 연산하면
1110^10 => 1100
여기에 8을 다시 연산하면
1100^1000 => 100
으로 다시 4가 된다.즉, 동일한 2의 배수가 2번연산되면 해당 하는 자리에 1이 더해졌다가 빠지면서 0이되고,
원래대로 돌아가 1개만 있는 2의 배수만 남게 된다.
이와 같은 원래로 [4,1,2,1,2] 테스트 케이스를 넣어 실행하면 다음과 같이 처리된다.
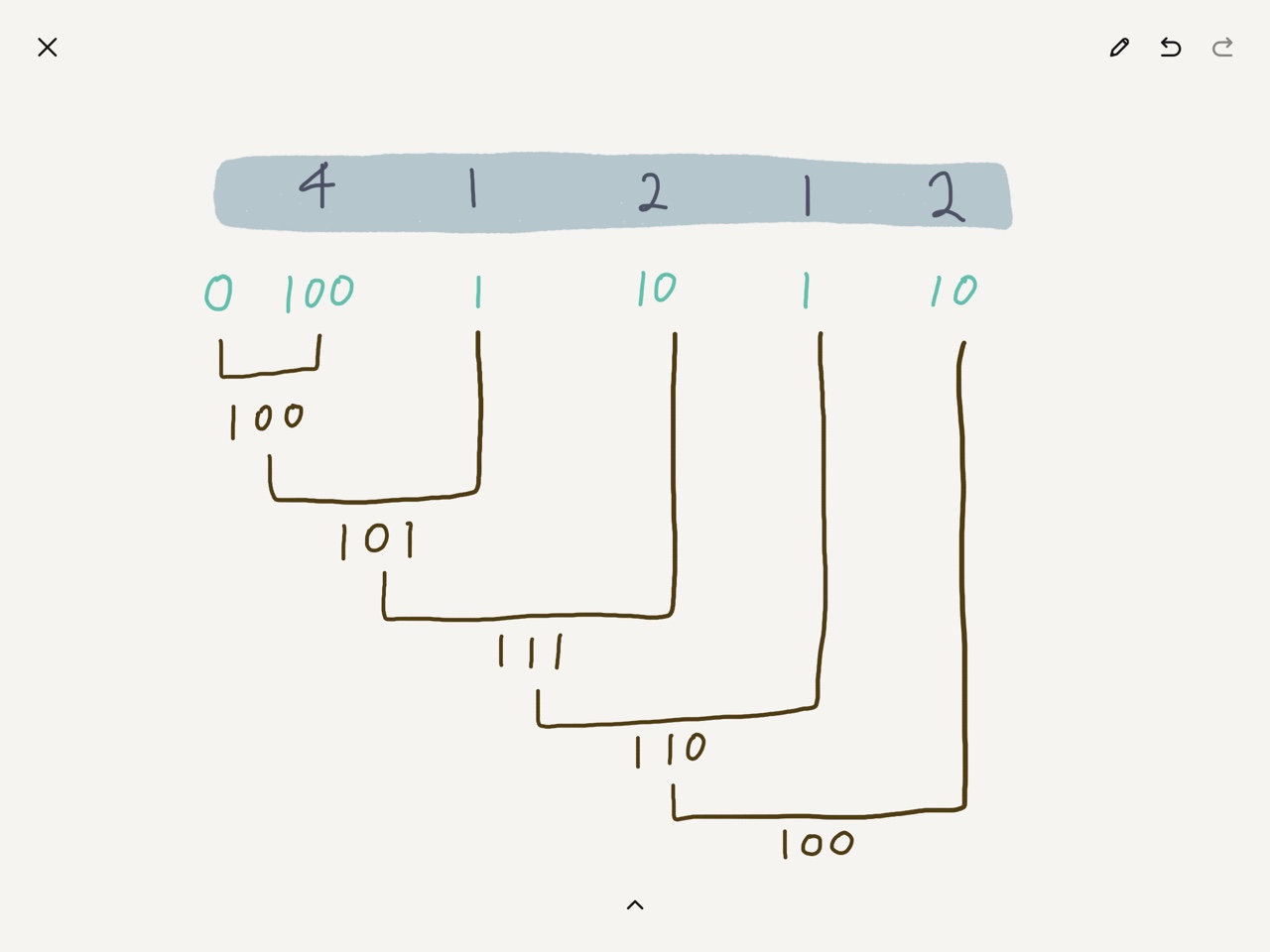
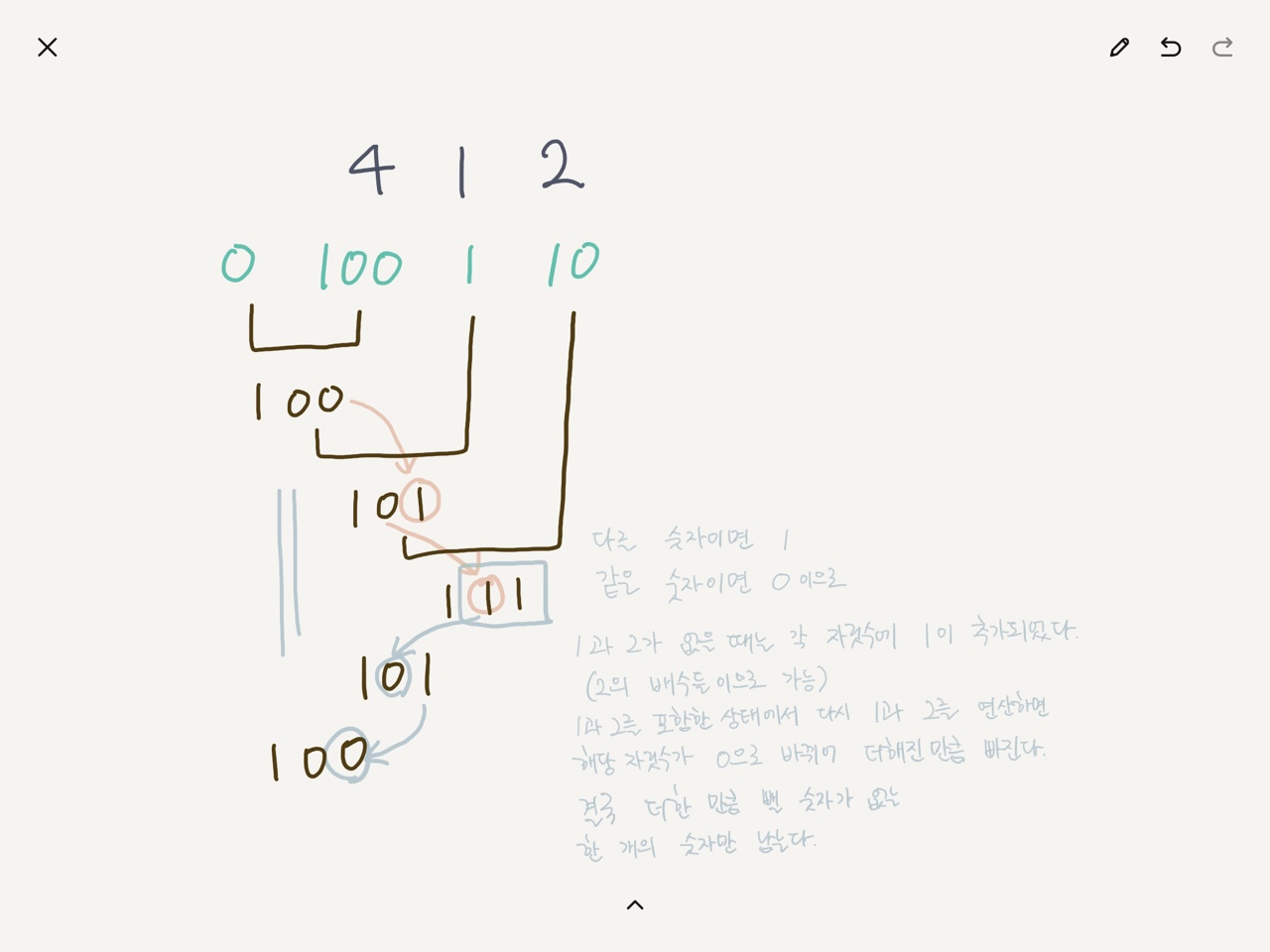
Result
Runtime
72 ms, faster than 95.73% of JavaScript online submissions for Single Number.
Memory Usage
41.3 MB, less than 83.27% of JavaScript online submissions for Single Number.
