벌써 4학년 2학기다 취업 시즌은 다가오는데 이제서야 코테 준비를 시작하려고 마음을 먹음 이제서야!!!!(왜 그랬니..) 솔직히 말하면 후회도 스럽고 마음이 무겁다.
주변 친구들을 보면 2학년, 3학년 때부터 코테 문제를 꾸준히 풀고, 깃허브에 기록도 잔뜩 쌓아놨다. 백준 티어도 나랑 비교할 수 없을 정도고 볼 때마다 나를 원망하게 된다... ㅋㅋㅋ
과거의 나 뭐했나 진짜로!!
괜히 놀고 미루다 주변 친구들이 서서히 취업하는 것을 보고 조급해진 것 같다.
내가 할 수 있을까, 이미 늦은 거 아닐까 생각을 이 글로 바꿔보고자 한다.
손 놓고 어버버 바보 처럼 있는 거보다 그냥 지금 당장 시작하는 것이다. 간다
🐣 시간 복잡도 표기법 알아보자
코딩 테스트의 핵심 중 하나는 문제마다 주어진 시간 복잡도를 고려해 적절한 알고리즘을 선택
- 시간 복잡도
- 알고리즘이 문제를 해결하는 데 걸리는 시간과 입력 데이터 크기 사이의 관게
시간 복잡도 정의하기
- 빅-오메가(Ω(n)) - 최선일 때(bese case)의 연산 횟수를 나타낸 표기법
- 빅-세타(Θ(n)) - 보통일 때(average case)의 연산 횟수를 나타낸 표기법
- 빅-오(O(n)) - 최악일 때(worst case)의 연산 횟수를 나타낸 표기법
- 빅오 표기법
- O(1) - 상수 시간, 입력 크기와 관계없이 일정한 시간이 걸림
- O(n) - 선형 시간, 입력 크기에 비례하여 시간이 증가
- O(n^2) - 이차 시간, 입력 크기가 두 배가 될 시간이 4배 증가하는 방식
- O(log n) - 로그 시간, 이진 탐색처럼 입력 크기가 커져도 시간이 천천히 증가하는 방식
- O(n log n) - 병합 정렬, 퀵 정렬과 같이 매우 효율적인 시간 복잡도
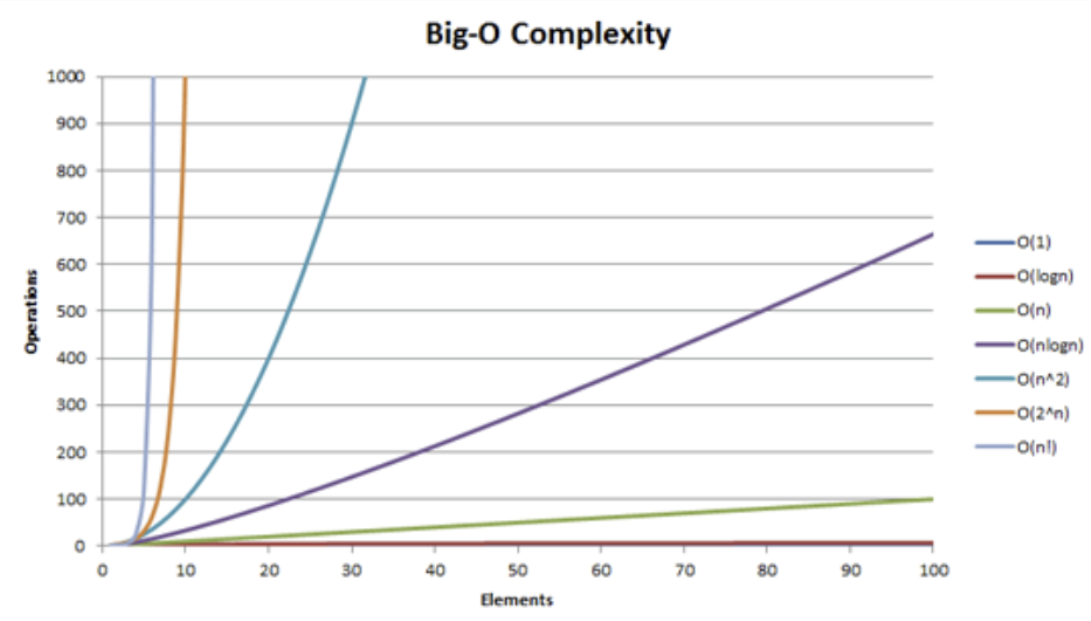
💡 코테에서는 빅-오(O(n))표기법을 기준으로 표현!!
🐣 시간 복잡도 활용하기
백준 2750번 - 수 정렬하기
첫째 줄에 수의 개수 N(1 <= N <= 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 수가 주어진다. 이 수는 절댓값이 1,000보다 작거나 같은 정수이다. 수는 중복되지 않는다.
시간 제한이 1초 이므로 이 조건을 만족하려면 1억 번 이하의 연산 횟수로 문제를 해결해야 함
시간 복잡도는 항상 최악일 때, 즉 데이터의 크기가 가장 클 때를 기준으로 정함
연산 횟수 계산 방법
- 연산 횟수 = 알고리즘 시간 복잡도 X 데이터의 크기
알고리즘 적합성 평가
- 버블 정렬(O(n²)) = (1,000)² = 1,000,000 < 100,000,000 → 적합 알고리즘
- 병합 정렬(O(n log n)) = 1,000log(1,000) = 약 10,000 < 100,000,000 → 적합
둘 다 적합 하지만 N이 10,000으로 보면 버블 정렬은 적합 하지 않음을 알 수 있다
따라서 N이 커저도 안정적이고 여유로운 벙합 정렬을 사용하도록 하자!!
🐣 디버깅 활용 사례
- 변수 초기화 오류 찾기
- 반복문에서 인덱스 범위 지정 오류 찾기
- 잘못된 변수 사용 오류 찾기
- 자료형 범위 오류 찾기
💡 자료형은 처음부터 Long형으로 선언하자!

