🐣 백준 11660 - 구간 합 구하기 5
1. 문제
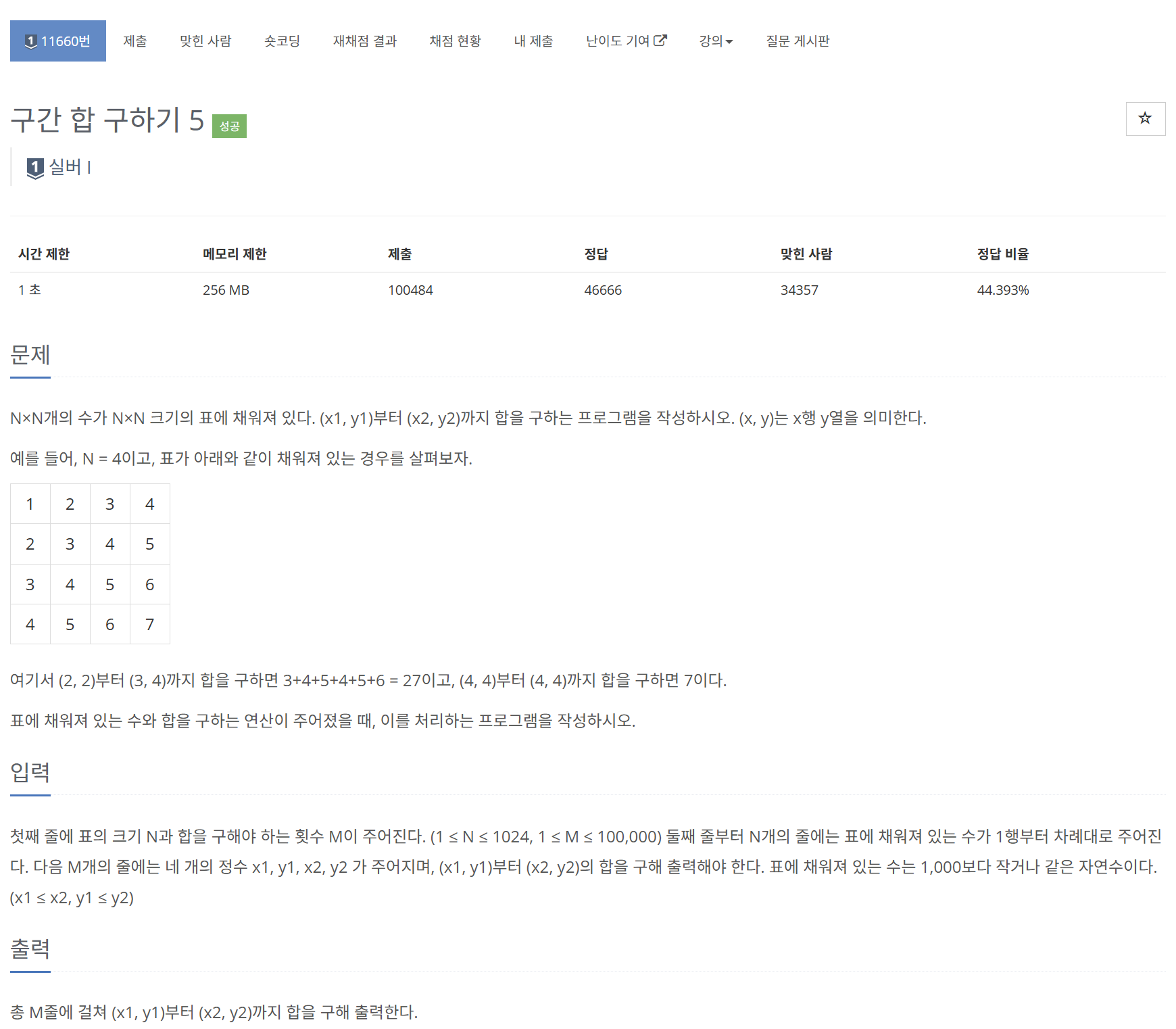
- N * N 크기의 표가 주어짐
- N * N 배열에서 M개의 (x1, y1) 부터 (x2, y2)까지의 구간 합을 구하는 문제
2. 입력
- 1번째 줄은 표의 크기 N 입력, 구간 합 구해야 하는 횟수 M 입력
(1 <= N <= 1024), (1 <= M <= 100,000) - 2번째 줄은 원본 배열 1행부터 입력
- M개의 줄에는 4개의 정수 x1, y1, x2, y2 입력 (정수 4개는 1,000보다 작거나 같은 자연수)
3. 출력
- 입력 받은 4개의 정수 (x1, y1) 부터 (x2, y2)의 합을 출력
4. 시간 복잡도
-
배열을 채우기 위해 N * N개의 칸을 모두 한 번씩 방문 하기때문에 -> O(N^2)
-
누적합 배열을 이용해서 4번만 더하고 빼면 되기 때문에 -> O(M)
💡 O(N^2 + M) 이 시간 복잡도
-
최악의 경우 : 1024 * 1024 + 100,000 약 110만 번 계산이면 될 것 같다..
5. 문제 분석
예제 입력 2,2,3,4를 보고 함께 풀어보자 - 사진은 원본 배열 A[i][j]임
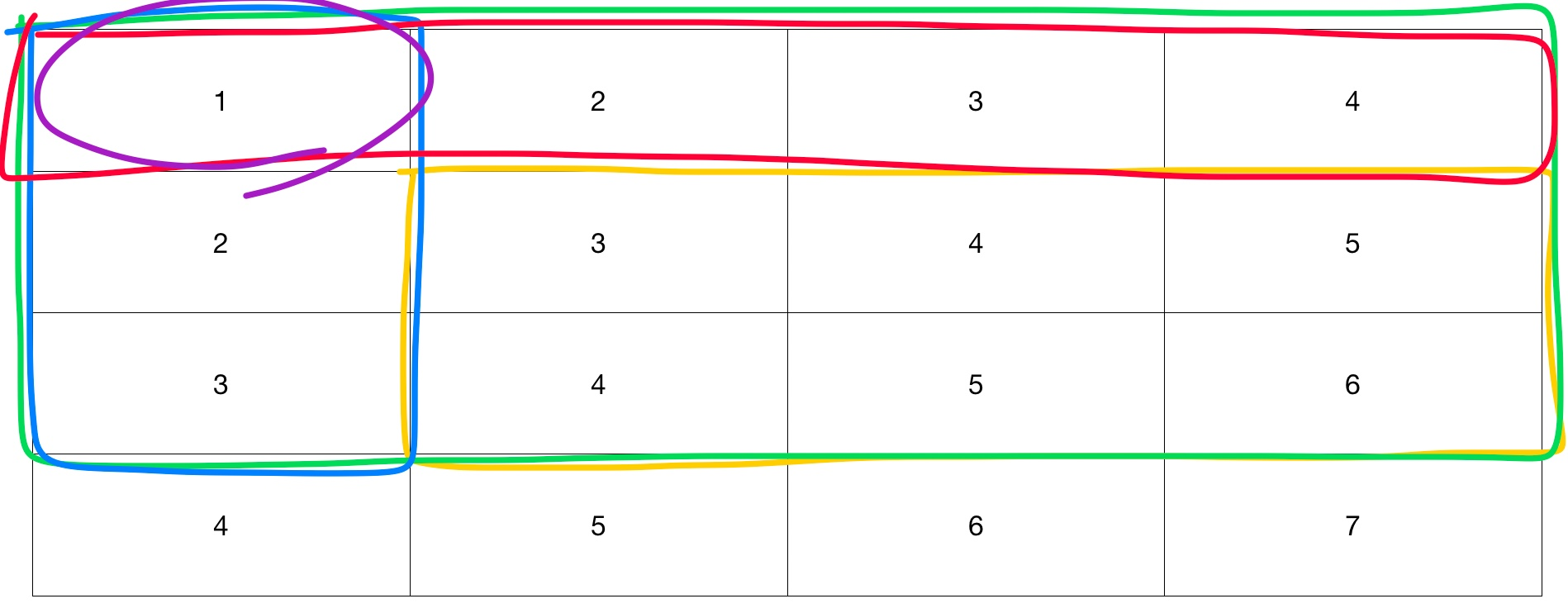
우리가 구해야하는 것은 노란색 박스이다
그전에 구간 합 배열을 채워야지 노란색 박스의 구간 합을 구할 수 있다
D[i][j]의 값을 채우는 구간 합 공식
D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j]
위 공식을 가지고 구간 합 배열을 완성 시켜주면 사진이 나온다
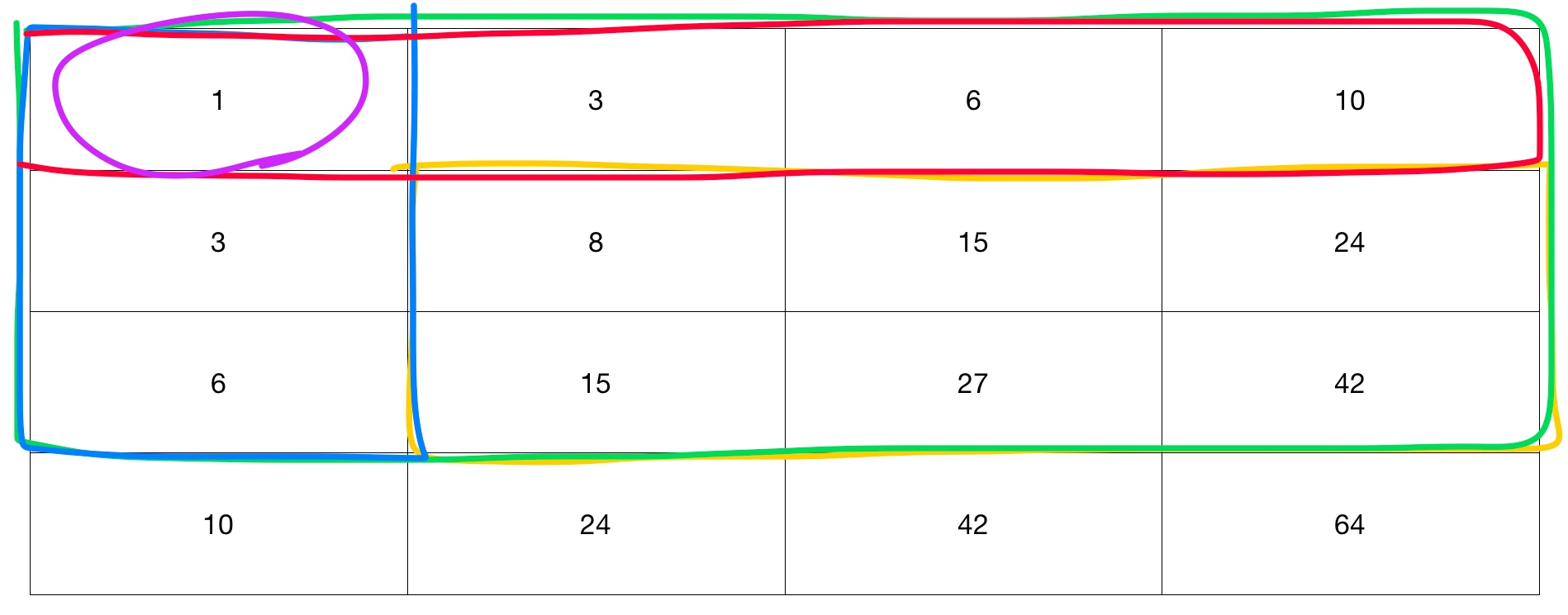
노란색 박스의 구간 합을 구하려면
녹색 박스 - 파란색 박스 - 빨간색 박스 + 보라색 박스를 구하면 된다
- 입력 - (x1 = 2, y1 = 2, x2 = 3 ,y2 = 4)
D[3][4] - D[3][1] - D[1][4] + D[1][1]= 노란색 박스 가 나오게 된다
질의 x1, y1, x2, y2에 대한 답을 구간 합으로 구하는 방법
D[x2][y2] - D[x2][y1 - 1] - D[x1 - 1][y2] + D[x1 - 1][y1 - 1]
6. 슈도 코드
1. N * N (배열 크기), M (질의 수) 저장
2. for(N만큼 반복) {
2-1. for(N만큼 반복) {
2-2. 원본 배열 저장
}
}
3. for(N만큼 반복) {
3-1. for(N만큼 반복) {
3-2. 구간 합 배열 저장
}
}
4. for(M만큼 반복) {
4-1. 질의 숫자 저장
4-2. 구간 합 배열 결과 저장 및 출력
}7. 코드 구현
package dataSource;
import java.io.*;
import java.util.StringTokenizer;
public class No_11660 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int A[][] = new int[N+1][N+1];
for(int i = 1; i <= N; i++) {
st = new StringTokenizer(br.readLine());
for(int j = 1; j <= N; j++) {
A[i][j] = Integer.parseInt(st.nextToken());
}
}
int D[][] = new int[N+1][N+1];
for(int i = 1; i<=N; i++ ) {
for(int j = 1; j<=N; j++) {
D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j];
}
}
for(int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
int result = D[x2][y2] - D[x2][y1 - 1] - D[x1 - 1][y2] + D[x1 - 1][y1 - 1];
System.out.println(result);
}
}
}