[LeetCode/Python3] Pseudo-Palindromic Paths in a Binary Tree

Problem

Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be pseudo-palindromic if at least one permutation of the node values in the path is a palindrome.

Return the number of pseudo-palindromic paths going from the root node to leaf nodes.

Example 1:

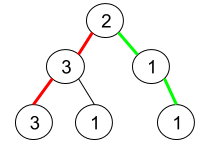
Input: root = [2,3,1,3,1,null,1]
Output: 2
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path [2,3,3], the green path [2,1,1], and the path [2,3,1]. Among these paths only red path and green path are pseudo-palindromic paths since the red path [2,3,3] can be rearranged in 3,2,3 and the green path [2,1,1] can be rearranged in 1,2,1.

문제에 주어진 2진 트리의 root에서 시작하는 경로의 노드가 palindrome에 해당하는 경로의 개수를 구하는 문제이다. palindrome은 좌우가 똑같은 문자열로 example1의 경로를 보면 2, 1, 1과 2, 3, 3이 해당한다. 두 경로는 각각 1, 2, 1과 3, 2, 3 형태의 palindrome을 만들 수 있다.

Solution

• 먼저 root에서 시작하는 경로를 모두 구해야 하는데 dfs를 이용해 재귀형태로 구현했다.
• 현재 노드의 자식 노드가 존재한다면 왼쪽 자식노드부터 먼저 탐색한다. 탐색 전에 자식노드의 val의 개수를 1 증가시키고, 탐색이 끝나면 val의 개수를 1 감소시킨다.
• 현재 노드가 자식이 없는 리프노드이면 현재까지의 경로가 palindrome인지 확인한다.
• palindrome은 두 가지 조건 중 하나를 만족해야 한다.
  1. 각 숫자의 개수가 모두 짝수
  2. 한 가지의 숫자의 개수만 홀수이며 나머지 숫자의 개수는 모두 짝수
• palindrome이 맞다면 answer의 개수를 하나 증가시킨다

Python Code

from collections import defaultdict

class Solution:
    def pseudoPalindromicPaths (self, root: Optional[TreeNode]) -> int:
        answer = 0
        def is_palindromic(digit_count: dict):
            odd = False
            for count in digit_count.values():
                if count % 2 > 0 and not odd:
                    odd = True
                elif count % 2 > 0 and odd:
                    return False
            return True
        
        def dfs(digit_count: dict, curr: Optional[TreeNode]):
            if not curr.left and not curr.right and is_palindromic(digit_count):
                nonlocal answer
                answer += 1
            if curr.left:
                digit_count[curr.left.val] += 1
                dfs(digit_count, curr.left)
                digit_count[curr.left.val] -= 1
            if curr.right:
                digit_count[curr.right.val] += 1
                dfs(digit_count, curr.right)
                digit_count[curr.right.val] -= 1
        
        digit_count = defaultdict(int)
        digit_count[root.val] = 1
        dfs(digit_count, root)
        return answer

• defaultdict를 이용하면 새로운 값을 넣을 때 초기화를 할 필요가 없다.