1주차 2번(Fly me to the Alpha Centauri)

이효균·2021년 5월 21일

알고리즘

스파르타코딩클럽-스파르탄365

목록 보기

7/9

1.문제 링크

https://www.acmicpc.net/problem/1011

2. 풀이 전 계획과 생각

어떤 유형의 문제이고, 어떤 방식의 풀이를 사용할지 고민하기
모든 경우의 수를 고려해야하는 문제인지
모든 경우의 수를 고려할 수 없다면, 어떤 규칙이 있는지 파악하기

2-1. 풀이를 위한 접근방식

전 단계의 이동거리는 다음단계의 이동거리를 결정한다.

첫번째 이동거리와 맨 마지막 이동거리는 반드시 1이다.
특히 마지막 이동거리의 제한조건으로 중간에서의 이동거리 조정이 필요!

중간 이동거리 조정은 단순한 조건문과 반복문으로 구현이 불가!
따라서 각 이동거리와 작동횟수간 규칙을 구하는 수열문제!

2-2. 규칙성 찾기

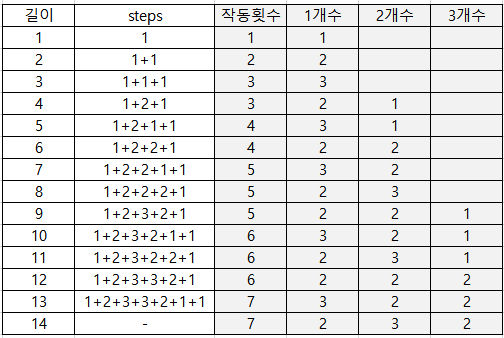
길이가 늘어남에 이동거리 steps와 작동횟수
▶ steps는 규칙성이 없고, 길이와 작동횟수가 핵심포인트!

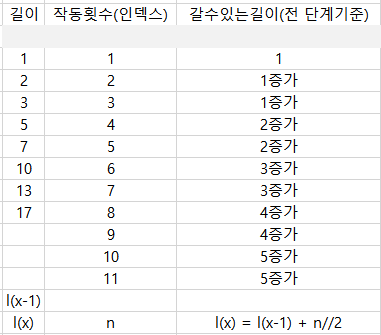
작동횟수를 인덱스화 하였을때, 그에 따른 길이가 규칙성이 존재한다.
▶ 해당 수열과 규칙성을 이용하여 memoization 방식으로 풀이!

2-3. 풀이

# T = test case
# x y = 각 지점
# 최초 작동시엔 이론상 -1 , 0 , 1 가능하며 실제론 반드시 1
# 최종 지점 도착 직전 마지막 이동거리는 반드시 1
# 작동장치횟수의 최소값



import sys

T = int(sys.stdin.readline())

array_test_case = []
for i in range(T):
    array_test_case.append(list(map(int, sys.stdin.readline().split())))

def get_minimum_value(T, array_test_case):

    for i in range(T):
        length = array_test_case[i][1] - array_test_case[i][0]

        main_process_in_function(length)


def main_process_in_function(length):
    max_length_for_each_operation = []
    for j in range(1, length + 1):
        if j == 1:
            max_length_for_each_operation.append(1)
        else:
            max_length_for_each_operation.append(max(max_length_for_each_operation) + j // 2)
            if max(max_length_for_each_operation) < length:
                continue
            elif max(max_length_for_each_operation) == length:
                print(j)
                break
            else:
                print(j - 1)  # 해당 인덱스에 기재된 길이부터 횟수가 증가, 그 이전의 인덱스까지가 유효한 길이
                break


get_minimum_value(T, array_test_case)

4. 풀이하면서 고민했던 점

규칙성이 있는지 없는지 빠른 시간내 파악하는 것이 중요!!
모든 경우의 수를 탐색하는 것이 불가능할 경우,
탐색로직 구현이 불가능할 경우엔 반드시 규칙성이 존재한다!!
알고리즘을 구현하는데 너무 시간이 오래걸린다
다른 방향으로 생각하는 것도 중요하지만, 시간을 절약하는 것도 매우 중요하다.
10분내외로 생각하고 알고리즘 구현하는 것까지 가능하도록 꾸준히 연습해보자.