4주차 1번(파도반 수열)

Hyo Kyun Lee·2021년 5월 3일

알고리즘

스파르타코딩클럽-스파르탄365

목록 보기

3/9

1.문제 링크

https://www.acmicpc.net/problem/9461

2. 풀이 전 계획과 생각

동적계획법 개념을 정확히 이해하고 문제에 맞게 구현하기
배열에 값을 저장하고 이후에 해당 값들을 사용한다는 점!
클린코드 : 알고리즘을 먼저 구현한후에 리팩토링 해보기

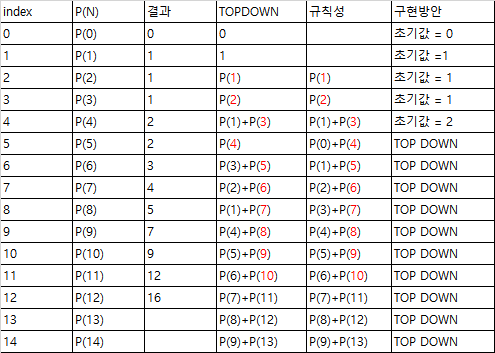
3-1. 규칙성찾기

방식 : TOP DOWN
규칙성 : P(N) = P(N-5) + P(N-1) *N=5부터
초기값 설정 필요 : N=0~4

3-2. 동적계획법을 이용한 풀이

# 동적계획법
# T = the number of test case
# N = index

#변수 N을 입력받아 결과를 반환해주는 로직
def P(N):
    array_memoization = [0] * (N + 1)

    result = Dynamic_programming(array_memoization)[N]

    return result

#동적계획법을 구현하는 로직
def Dynamic_programming(array_memoization):
    i = 0
    while i < (len(array_memoization)):
        if i == 0:
            array_memoization[i] = 0
        elif i == 1:
            array_memoization[i] = 1
        elif i == 2:
            array_memoization[i] = 1
        elif i == 3:
            array_memoization[i] = 1
        elif i == 4:
            array_memoization[i] = 2
        else:
            array_memoization[i] = array_memoization[i - 5] + array_memoization[i - 1]
        i = i + 1

    return array_memoization

print(P(6))
print(P(12))

3-3. 풀이하면서 참조한 링크

https://coding-all.tistory.com/2
https://kamang-it.tistory.com/entry/AlgorithmDynamic-Programming%EB%8F%99%EC%A0%81%EA%B3%84%ED%9A%8D%EB%B2%95%EB%8B%A4%EC%9D%B4%EB%82%98%EB%AF%B9-%ED%94%84%EB%A1%9C%EA%B7%B8%EB%9E%98%EB%B0%8D%EA%B3%BC-%EB%A9%94%EB%AA%A8%EC%9D%B4%EC%A0%9C%EC%9D%B4%EC%85%98memoization-%ED%83%80%EB%B7%B8%EB%A0%88%EC%9D%B4%EC%85%98tabulation

4. 풀이하면서 고민했던 점

test cast 개수인 T를 길이로 하는 링크드리스트를 만들고 P(N)을 해당 리스트에 넣어 결과를 출력해본다
알고리즘을 구현하는데 너무 시간이 오래걸린다
다른 방향으로 생각하는 것도 중요하지만, 시간을 절약하는 것도 매우 중요하다.
10분내외로 생각하고 알고리즘 구현하는 것까지 가능하도록 꾸준히 연습해보자.
클린코드
하나의 코드에 모든 기능을 담지말고, 기능을 최대한 분산한다.
▶변수 N을 입력받아 결과를 반환해주는 로직
▶동적계획법을 구현하는 로직
가독성이 좋은 코드, 이해가 쉬운 코드의 조건들을 생각해보자.

5. 문제를 풀고 알게된 개념 및 소감

동적계획법이란
큰 문제를 작은 문제로 나누어서 푼다 는 개념은 곧 "작은 답"들을 활용하여 "큰 문제"를 푼다 와 같다.
memoization
최종 큰 답을 구하는데 작은 답들을 저장하고 활용하는 로직
동적계획법의 가장 중요한 개념!
TOP DOWN, BOTTOM UP 모두 사용되는 개념!
TOP DOWN
최종단계의 답을 구하기위해 위(=최종단계)에서부터 내려오면서 저장한 값(=작은 답)을 활용하는 방식
ex 6번째 값을 구하기 위해 5,4,...하위단계의 값들중 필요한 값들을 구해나가며, 필요한 하위 단계 값들을 구했으면 로직 종료
BOTTOM UP / Tabulation
최종단계의 답을 구하기위해 처음부터 최종단계까지 모든 값들을 저장하면서 구해나가는 방식
ex 6번째 값을 구하기 위해 1,2,3,...하위단계부터 값들을 모두 구해 나간다.