앞서 data link layer는 Data-link-control sublayer와 Media-access-control sublayer 2가지로 나눌 수 있다고 설명했다
그리고 이 중에서 Data-link-control sublayer의 대표적인 2가지 기능으로 아래의 2가지가 있다
- Framing
- Error control
Error Control
Error control은 error detection과 error correction을 포함한다
간섭에 의하여 bit가 바뀌는 error가 발생할 수 있다
그렇다면 어떤 error들이 발생할 수 있을까?
types of error
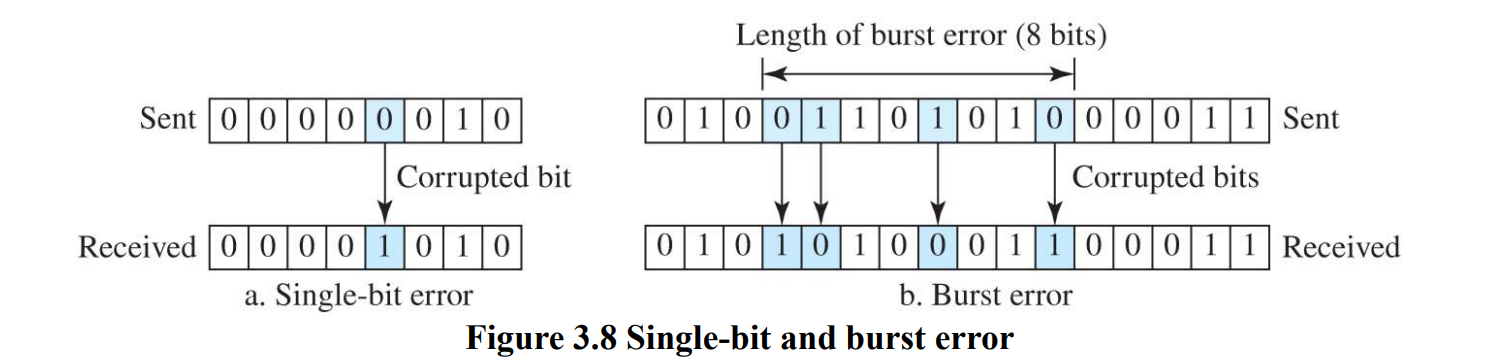
- single-bit error
- burst error
single-bit error
주어진 data unit(byte, character, packet)에서 1bit가 에러난 것
burst error
주어진 data unit에서 error가 자주 난 것
정확이 2개 연속으로 나야 burst error가 아니라 그냥 슥 보고 bit error가 자주 있으면 다 묶어서 burst error 라고 함
error detection과 error correction
error detection과 error correction을 위하여 추가적인 bit들을 데이터에 추가하여 보낸다
이렇게 추가하는 data를 redundancy라고 한다
당연히 detection 보다는 correction이 어렵고 redundancy가 길다
뭐가 더 좋냐는 상황에 따라 다르기 때문에 정할 수 없음
- error 숫자나 message 크기가 중요한 요소임
그러면 여기서 redundancy는 어떤 기준으로 만드는가?
redundancy는 다양한 코딩 기법으로 만들어낸다
- Block Coding
- Parity-Check Code
- Cyclic Codes
Block Coding
k-bit block으로 n-bit block을 만들기 때문에 block coding이라고 한다
순서
1. message를 datawords라는 k-bit block들로 나눈다
2. 각각의 block에 r bit의 redundancy를 추가한다
여기서 n(k+r) bit의 block은 code words라고 불린다
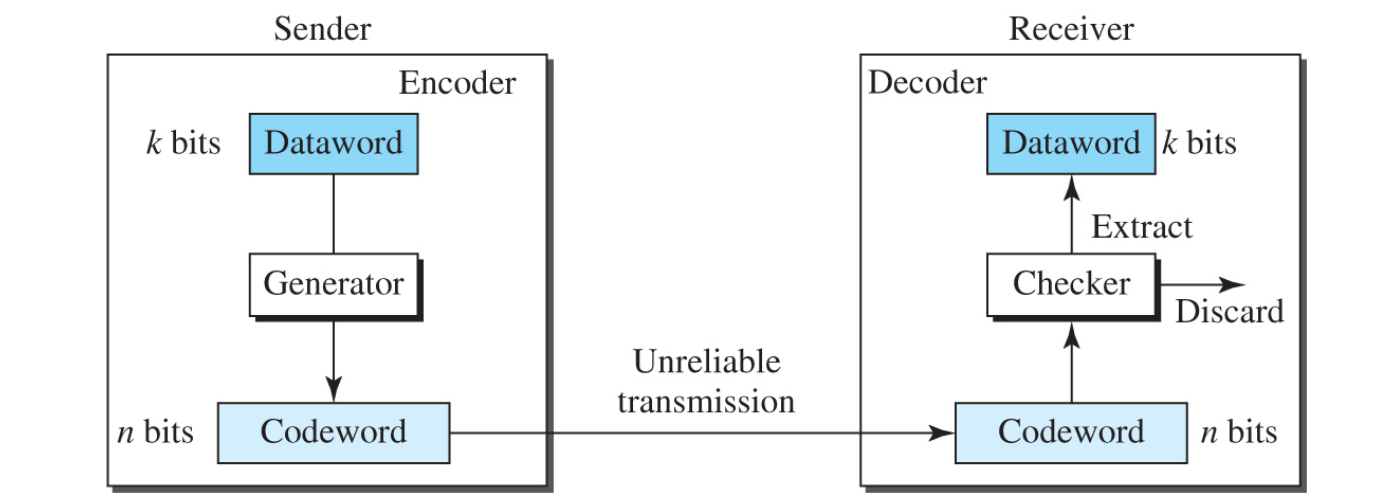
Genertor에서는 r bit의 redundancy를 생성하고 Checker는 error 여부와 있었으면 어디에 있었는지를 체크함
(어떤 r bit를 생성하는지에 대한 원리는 나중에 나옴)
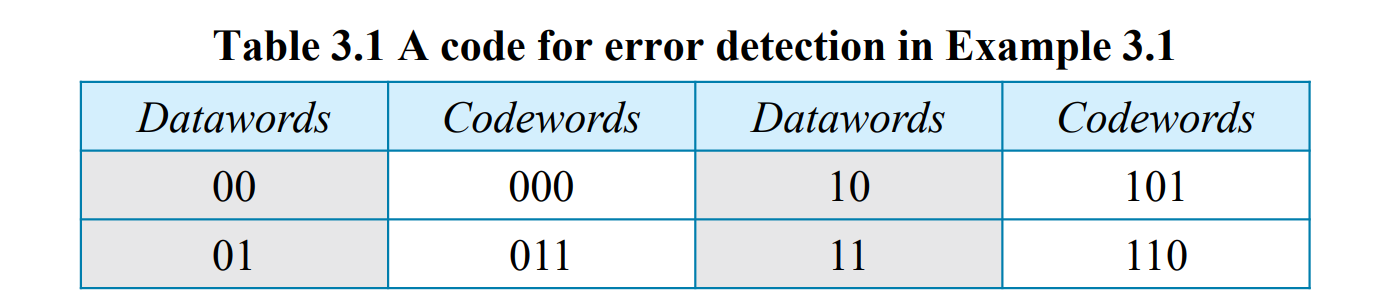
위의 예시는 k = 2, r = 1, n = 3으로 설정한 table임
header나 trailer에 넣는 것이 아니라 data 자체를 match table에서 해당하는 codewords로 바꾸어 넣는거임
이렇게 해서 011을 수신하면 이를 checker를 통해서 00이라는 datawords를 얻음
첫번째 bit에 error가 나서 111을 수신하면 이 데이터는 table에 없으니까 버림
근데 여기서 만일 두번째, 세번째 bit가 error가 나서 000을 수신하면 이는 table에 있기 때문에 00으로 받아들이게 됨 (잘못된 데이터를 받아들이는 문제)
위의 경우에는 r = 1로 1 bit만 붙이기 때문에 detection의 성능이 떨어지게 됨
Hamming Distance
error control의 중요한 컨셉중에 하나로, 길이가 같은 두 비트열의 값이 다른 비트 개수를 나타낸다
즉, 두 bit들의 XOR 연산을 통해서 나온 결과값의 1의 개수를 의미함

Minimum Hamming Distance
codewords의 집합 속에서 가능한 codeword 쌍들의 가장 작은 hamming distance가 minimum hamming distance 이다
s개의 error까지 탐지해야 한다면 codewords set의 minimum distance는 s+1 보다 커야한다
예를들어, minimum hamming distance가 3이면 2bit까지의 오류를 찾을 수 있다는 뜻
이는 codewords set의 성능을 측정하는 지표가 됨
Linear Block Codes
두개의 유효한 codeworkds를 XOR 연산을 하면 다른 유효한 코드를 만들 수 있는 코드들이고 오늘날 사용되는 block code들은 거의 다 linear block code의 일부이다
이런 linear block code에서 minimum hamming distance는 모든 bit가 0인 codeword를 제외한 codeword set에서 1의 개수가 가장 작은 codeword의 1의 개수이다

위의 table은 linear code block의 일부로 이루어져있고 그렇다면 hamming distance(dmin)는 1이 가장 작은 codeword의 1의 개수인 2이다 -> 따라서 1bit의 오류를 탐지할 수 있다
Parity-Check Code
가장 쉬운 error check 방법 중 하나로 k bit datawords에 1bit를 더하여 n(k+1)bit의 codeword를 만드는 것이다
이때 추가되는 1bit를 parity bit라고 하고, 이 parity bit는 nbit의 codeword에서 1의 개수가 짝수가 되도록 만든다
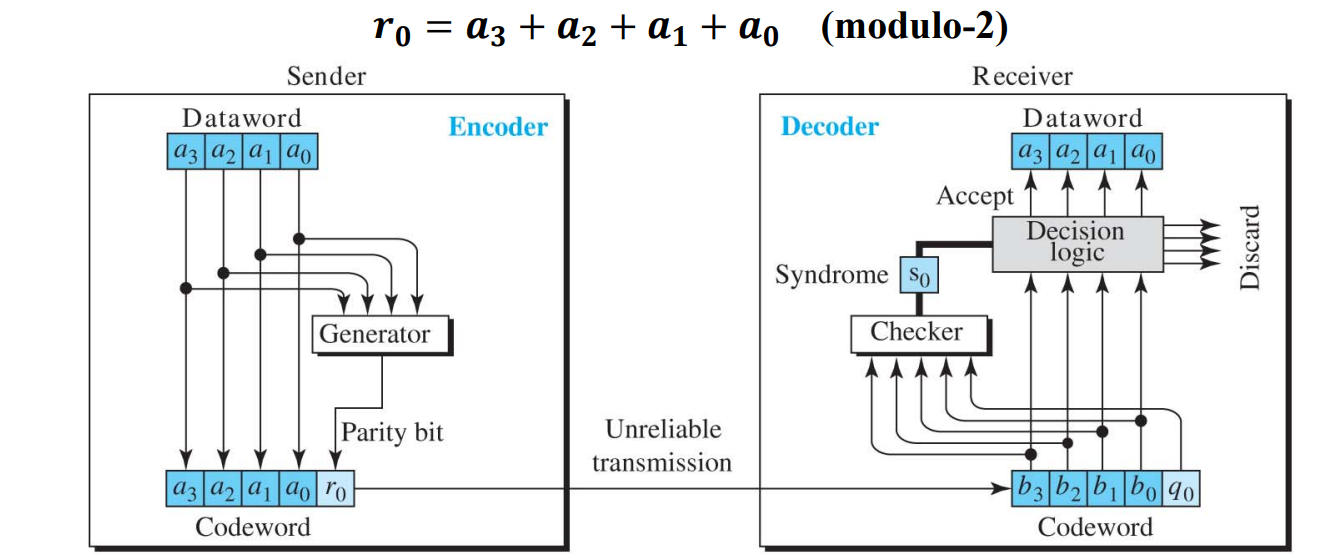
위 그림에서, Generator는 4bit dataword를 input으로 받아 modulo 연산을 통해 parity bit r0를 생성하고, sender는 parity bit와 dataword를 합친 5bit codeword를 전송한다
receiver는 5 bit codeword를 Checker에 넣어서 똑같이 modulo 연산을 수행하고 Syndrome을 생성한다.
이때 syndrome이 1이라는 말은 codeword의 1이 짝수개가 아니라는 말이므로 데이터를 버리고 syndrome이 0이라면 data를 accept 한다
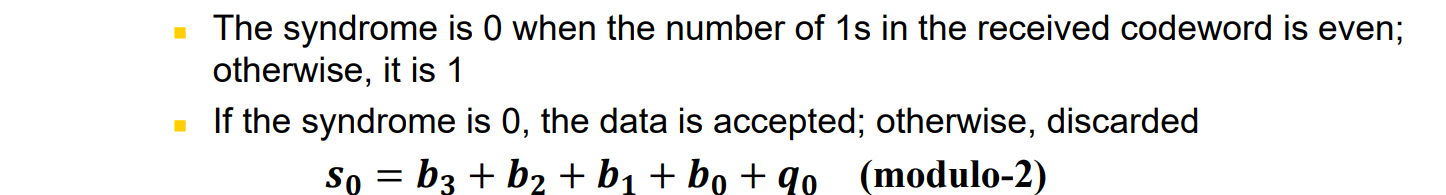
이 방법은 error가 났다 안났다만 확인할 수 있지 어디서 났는지는 체크할 수 없기 때문에 dataword가 아닌 parity bit가 error가 나도 데이터를 discard 한다
또한 짝수개의 error가 발생하면 이를 알아차릴 수 없기 때문에, syndrome이 1인 홀수개의 error만 탐지할 수 있다
장점으로는 1bit를 추가함으로써 많은 error를 찾을 수 있다는 점!
Cyclic Codes
특정한 codeword를 왼쪽이나 오른쪽으로 shift 하여 다른 codeword를 얻는 것
만일 1011000을 cyclically left-shift를 수행하면 0110001이 된다
cyclic code의 대표적인 예로 cyclic redundancy check(CRC)를 살펴보자
Cyclic redundancy check (CRC)
주로 LAN이나 WAN에서 사용하는 방식으로 나눗셈을 통하여 codeword를 생성한다
나눗셈은 순환적 bit shift와 XOR 연산의 결합이므로 이는 Cyclic code의 특성에 만족한다
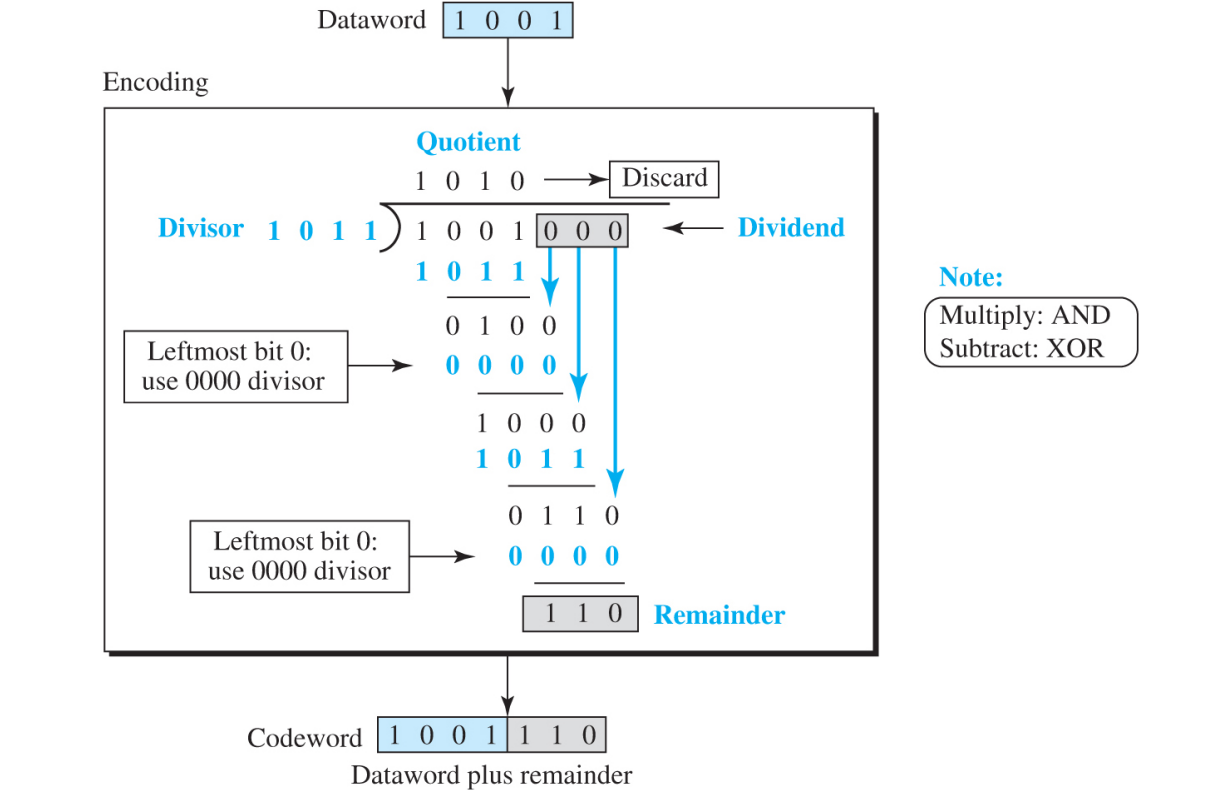
CRC에서 codeword를 전송하는 과정
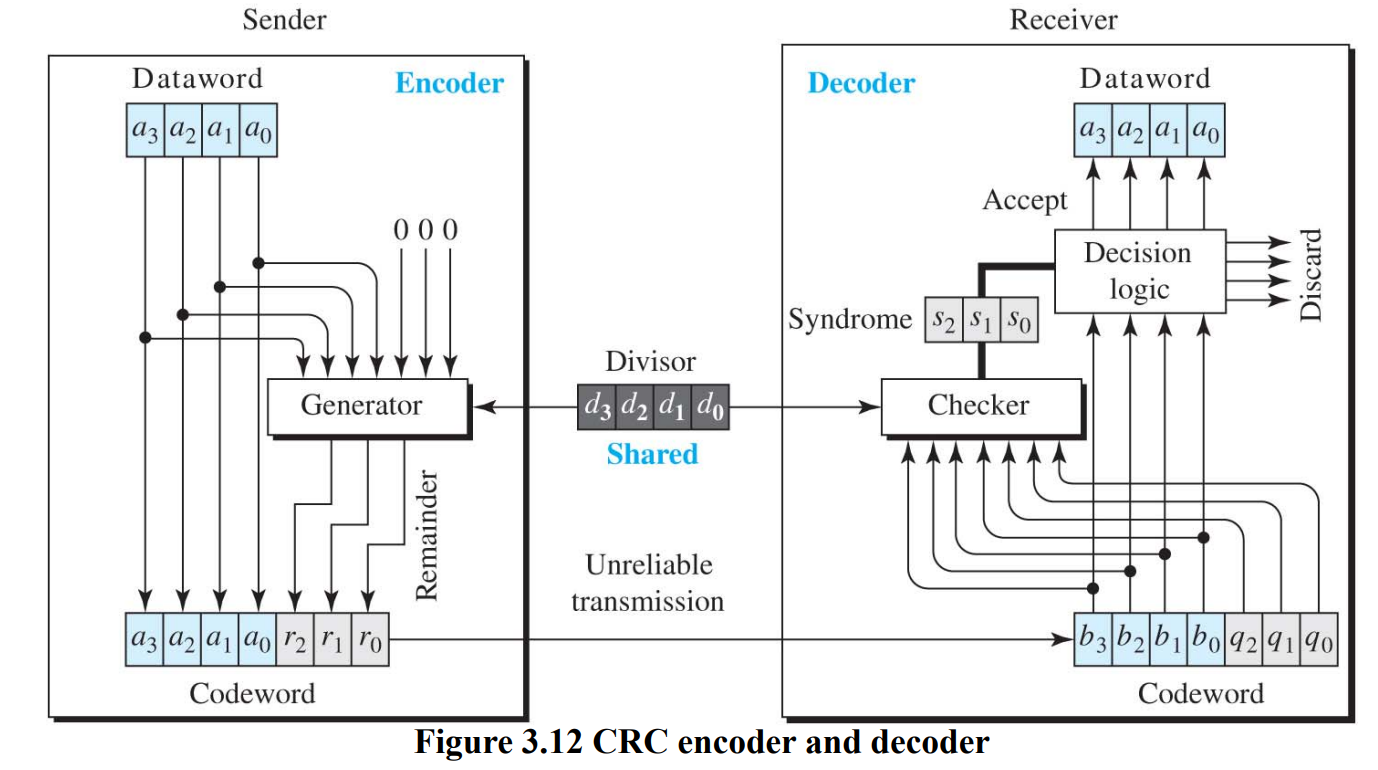
위의 예시 설명
Encoder:
dataword 가 4 bit 이고 codeword가 7bit라면 n - k = 7 - 4 = 3이므로 3bit의 data를 가장 오른쪽에 더하여 codeword를 생성하면 된다
따라서 000이라는 데이터를 추가하여 총 7bit의 data가 generator로 입력된다
generator는 n-k+1 = 7-4+1 = 4bit의 divisor를 사용하여 나눗셈 연산을 수행하고 나머지인 r2r1r0를 data word에 붙인다 (몫은 버림)
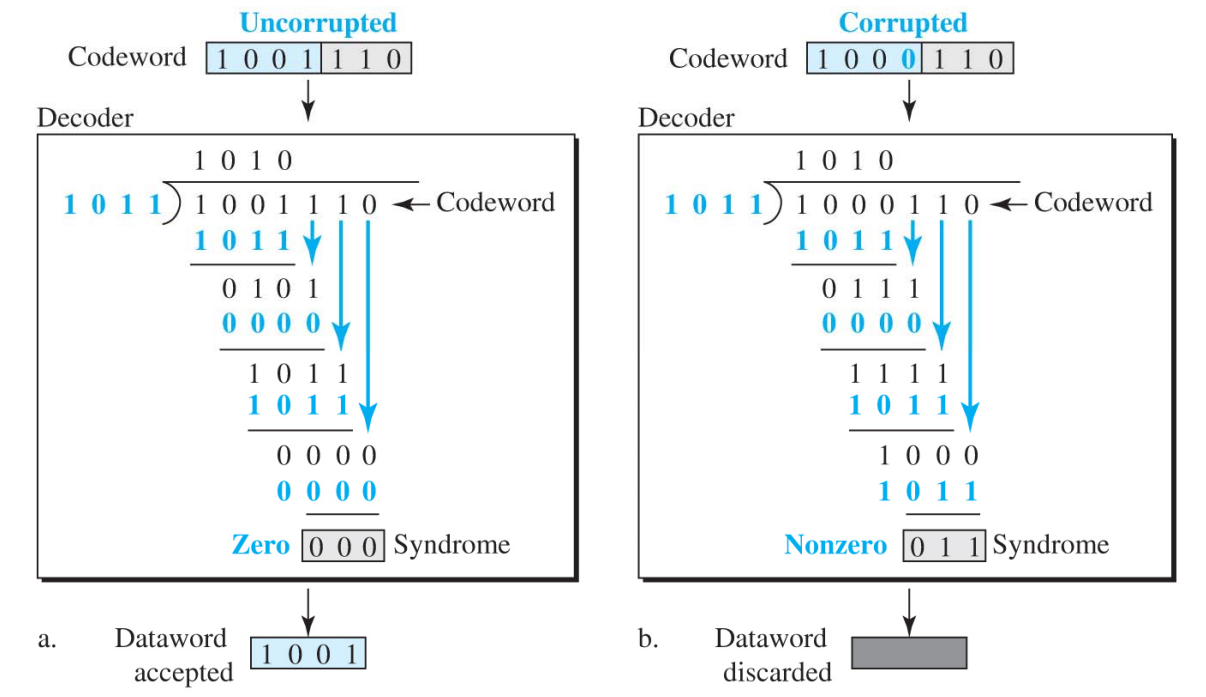
Decoder:
codeword를 받으면 n = 7bit 모두를 checker에 넘겨준다
checker는 똑같이 divisor를 사용하여 나눗셈 연산을 수행하고 그 결과가 0이라면 앞의 k bit를 accept 하고 아니라면 버린다
sender와 reciever가 공유하는 divisor로 나눈다
Encoder와 Decoder는 이렇게 계산을 일일이 할 수도 있고 이미 모든 dataword에 대해 계산을 한 값을 match table로 정리하여 찾아서 할 수도 있다
Divisor
여기서 그러면 divisor는 어떻게 정할 것인가?
아래 표와 같이 표준 나눗셈 연산자가 있다
나눗셈 연산자의 Name의 숫자는 나눗셈 연산자를 나타내는 다항식의 가장 높은 차수를 나타내기 때문에 bit의 수는 name 옆에 적힌 수보다 항상 1만큼 많다
즉 CRC-8은 9bit를 가지고 CRC-32는 33bit를 가진다
그리고 CRC-8은 나누는 divisor가 9bit이기 때문에 8bit가 remainder 가 된다
뿐만 아니라 divisor는 최소한 2bit를 가져야 하고 가장 오른쪽과 왼쪽의 bit는 모두 1이어야 하는 요구사항을 가지기도 한다
Performance of CRC
- single error는 모두 찾을 수 있다
- odd number of error는 다는 찾을 수 없고 특정 조건 하에서만 찾을 수 있다
(even 이슈는 언급하지 않음)- burst error 탐지는 burst error의 길이가 L이고, 추가로 붙인 remainder의 길이가 r일때 아래와 같은 식을 만족한다
- L <= r 이면 탐지할 수 있다
- L = r +1 이면 1-(0.5의 r-1승)의 확률로 찾을 수 있다
- L > r + 1 이면 1-(0.5의 r승)의 확률로 찾을 수 있다
사이클릭 코드의 장점
사이클릭 코드는 하드웨어와 소프트웨어에서 쉽게 구현될 수 있고, 특히 하드웨어에서 구현될 때 빠르게 동작한다
+) Checksum
체크섬은 어떤 길이의 메시지에도 적용될 수 있는 오류 검출 기술로 network layer와 transport layer에서 주로 사용한다