| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞은 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 2 초 | 128 MB | 276 | 118 | 104 | 43.697% |
문제
2010년 노원구에 여러 층으로 이루어진 다리를 놓기로 결정했고 실제 디자인까지 완성하였다. 하지만 당연한 소리일지 모르지만 교각 없이 다리가 공중에 떠있을 수는 없기에 적절히 교각을 설치해야한다.
교각 설치 규칙은 다음과 같다. 다리의 양 끝을 다른 다리 위나 혹은 바닥에 설치해야하고 가능한한 교각의 길이는 최소로 하고 싶다. 단, 다리는 모두 수평으로 놓여있고 다리는 수직으로 세워야한다. 교각이 다른 교각과 교차하면 안된다.
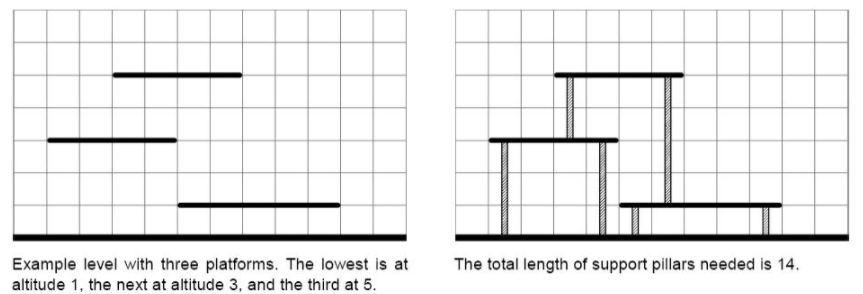
예는 위 그림과 같다. 왼쪽 그림은 디자인된 다리를 표시한 것이고 오른쪽 그림은 교각을 놓은 다리를 표시한 것이다. 그리고 교각의 총 길이는 14가 되는 것을 알 수 있다.
문제는 다리가 주어졌을 때 총 교각의 길이 합을 구하는 것이다.
입력
첫째 줄에 다리의 개수를 나타내는 정수 N(1≤N≤100)이 주어진다. 둘째 줄부터 N+1번째 줄까지 각 줄에 다리의 위치를 나타내는 세 정수 Y, X1, X2가 주어지는 이는 (X1, Y)부터 (X2, Y)까지 다리가 놓여있다는 의미이다. 모든 좌표는 10000을 넘지않는 자연수이다. 그리고 바닥의 Y좌표는 0이라고 가정한다. (X2 > X1+1)
출력
첫째 줄에 교각 길이의 총 합을 출력한다.
접근
x의 범위가 0 ~ 10000 이므로, 아래에서부터 다리를 놓아가면서 최대 높이를 저장하면 될 것 같다고 생각하였다.
실제로 다리가 겹치는 경우도 없고, 다리의 갯수도 최대 100개이기 때문에, 넉넉하게 구현하여도 괜찮았다.
골드 문제 치고 너무 쉬운 풀이가 아닌가? 하는 생각이 들었는데, 논리적으로 틀린 부분이 없기 때문에 그대로 구현하였다.
풀이
pair<int, pair<int, int>> 이런 자료형을 제일 싫어하지만, 굳이 구조체를 하나 만들기 싫어서 그냥 이렇게 진행하였다.
y축(높이)를 기준으로 배열을 정렬하였고, 순회하면서 x1좌표와 x2좌표에서의 교각 높이를 ans에 더해주었다.
그리고 x1 ~ x2에서의 높이(height 배열)을 초기화해주었다.
#include <bits/stdc++.h>
using namespace std;
#define ll long long int
#define FUP(i, a, b) for(int i = a; i <= b; i++)
#define FDOWN(i, a, b) for(int i = a; i >= b; i--)
#define MS(a, b) memset(a, b, sizeof(a))
#define ALL(v) v.begin(), v.end()
#define CIN(a) cin >> a;
#define CIN2(a, b) cin >> a >> b
#define CIN3(a, b, c) cin >> a >> b >> c
#define COUT(a) cout << a
#define COUT2(a, b) cout << a << ' ' << b
#define COUT3(a, b, c) cout << a << ' ' << b << ' ' << c
#define ENDL cout << '\n'
int dy[4] = { -1, 1, 0, 0 };
int dx[4] = { 0, 0, 1, -1 };
int N, ans = 0, height[10000];
pair<int, pair<int, int>> arr[100];
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
MS(height, 0);
CIN(N);
FUP(i, 0, N - 1)
{
CIN3(arr[i].first, arr[i].second.first, arr[i].second.second);
}
sort(arr, arr + N);
FUP(i, 0, N - 1)
{
int y = arr[i].first;
int left = arr[i].second.first;
int right = arr[i].second.second;
ans += (y - height[left]);
ans += (y - height[right - 1]);
FUP(h, left, right - 1) height[h] = y;
}
COUT(ans);
return 0;
}